Tema 2. Organización y representación de datos
Anuncio

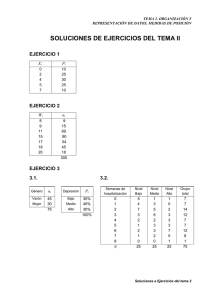
Análisis de Datos I Esquema del Tema 2 Tema 2. Organización y representación de datos 1. DISTRIBUCIÓN DE FRECUENCIAS 2. REPRESENTACIONES GRÁFICAS 3. MEDIDAS DE POSICIÓN: CENTILES 4. OTROS CUANTILES DECILES CUARTILES 5. EJERCICIOS __________________ Bibliografía: Tema 2 (pág. 45-83) Ejercicios recomendados: 1, 2, 5, 6, 9, 10, 12, 14, 16, 17, 20 y 21. Carmen Ximénez 1 Análisis de Datos I Esquema del Tema 2 1. DISTRIBUCIÓN DE FRECUENCIAS Xi X1 X2 .. . XN ni n1 n2 .. . nN Totales: N na n1 n1 + n2 .. . N pi n1 / N n2 / N .. . nN / N 1 Ejemplo A: Muestra de datos: 2 1 2 3 4 2 1 3 1 3 1 1 3 1 3 2 3 3 1 3 1 3 1 1 4 3 4 3 1 4 Ordenación de datos: pa p1 p1 + p2 .. . 1 Frecuencia absoluta (ni) Frecuencia absoluta acumulada (na) Frecuencia relativa (pi) Frecuencia relativa acumulada (pa) Xi ni na 1 2 3 4 : 11 5 14 5 35 11 16 30 35 pi 3 3 4 3 2 pa 0,31 0,31 0,14 0,45 0,40 0,85 0,14 1 1 Ejemplo B: Datos originales: 1 2 3 4 3 3 1 3 1 3 1 3 2 3 4 3 4 3 1 2 Distribución de frecuencias: ni na pi Xi 1 5 5 0,25 2 3 8 0,15 3 9 17 0,45 4 3 20 0,15 1 : N = 20 pa 0,25 0,40 0,85 1,00 2. REPRESENTACIONES GRÁFICAS Convenciones: 1) 2) 3) 4) 5) En las abscisas van siempre los valores y en las ordenadas las frecuencias La intersección es siempre el origen de los ejes Si los valores mínimos son muy grandes, cortar los ejes Incluir toda la información posible (leyendas) Si se incorporan dos representaciones en una sola gráfica, usar frecuencias relativas Variables nominales o cualitativas: Diagrama de pastel (y también de barras) Ejemplo 1: Género Xi ni Varón (1) 20 Mujer (2) 30 Carmen Ximénez pi 0,40 0,60 Varón Mujer 2 Análisis de Datos I Esquema del Tema 2 Variables ordinales: Diagrama de barras 60 pi 0,32 0,50 0,18 1 pa 0,32 0,82 1,00 50 Porcentaje Ejemplo 2: Satisfacción laboral Xi ni na Nada satisfecho 32 32 Medianamente 50 82 Muy satisfecho 18 100 N = 100 40 30 20 10 0 Nada Medio Mucho Grado de Satisfacción Variables Cuantitativas Discretas: Polígono de frecuencias (y también Diagrama de barras) Ejemplo 3: Nº aciertos en un test Xi ni na pi pa 1 9 9 0,45 0,45 2 3 12 0,15 0,60 3 2 14 0,10 0,70 4 1 15 0,05 0,75 5 5 20 0,25 1,00 10 Frecuencia 8 6 4 2 0 0 1 2 3 4 5 X Variables Cuantitativas Continuas: Histograma (y polígono de frecuencias) Ejemplo 4: Estatura (cm) Intervalos Xi ni 150 – 156 153 6 157 – 163 160 13 164 – 170 167 11 171 – 177 174 18 178 –184 181 8 ni 18 na 6 19 30 48 56 pi 0,11 0,23 0,20 0,32 0,14 16 pa 0,11 0,34 0,54 0,86 1,00 14 12 10 8 6 4 153 160 167 174 181 Xi Forma de la distribución: Propiedad de la Asimetría Propiedad de la Curtosis A A B C A. Asimetría positiva B. Simetría C. Asimetría negativa A. Leptocúrtica B. Mesocúrtica C. Platicúrtica B C X 0 1 2 3 Carmen Ximénez 4 5 6 X 0 1 2 3 4 5 6 3 Análisis de Datos I Esquema del Tema 2 Ejemplo: Baremo del peso de un recién nacido (niñas) 3. MEDIDAS DE POSICIÓN Peso (Kg.) 2,500 2,850 3,000 3,400 3,750 4,000 4,500 Las medidas de posición son estadísticos que indican la posición relativa que ocupa un sujeto en una distribución de frecuencias. Centil 3 10 25 50 75 90 97 LOS CENTILES, Ck Un centil es una puntuación (Xi) que deja debajo de sí un porcentaje acumulado (k) de sujetos de la distribución Ck Xi Pi 60% 35% 0 donde k = 1, 2, …, 99. C35 = 2 25% Xi C60 = 4 6 Los centiles… Son 99 valores la variable X que dividen la distribución en 100 secciones Indican la posición relativa de un sujeto en su grupo de referencia Dependen de la forma de la distribución de frecuencias Ejemplo 5: Xi 1 3 5 ni 5 12 3 na 5 17 20 pi 0,25 0,60 0,15 pa 0,25 0,85 1,00 C85 = 3 ... “La puntuación 3 es el centil 85” “El centil 85 es 3” “Un 85% de sujetos no superan la puntuación X = 3” “Un 15% superan la puntuación X = 3” Cálculo de centiles* Cálculo directo: Si se desea conocer el centil que corresponde a la puntuación: En puntuaciones observadas: kXi pa 100 En el ejemplo 5, tenemos que: C25 = 1, C85 = 3, etc. Cálculo inverso: Si se desea conocer la puntuación que corresponde a un centil: En puntuaciones observadas: Ck X i En el ejemplo 5, al centil 25 le corresponde la puntuación X = 1 ____________ * Nota. Para las puntuaciones no observadas (en el ejemplo 5, X = 2), los centiles pueden calcularse (tanto de forma directa como inversa) mediante unas “fórmulas de interpolación” (para más detalles véase el apéndice del tema 2 del libro, pág. 79). Dada la complejidad de estos cálculos, no veremos cómo obtenerlos a mano. Lo haremos con el SPSS. Carmen Ximénez 4 Análisis de Datos I Esquema del Tema 2 Ejemplo 6: Uso de los centiles como baremo 4. OTROS CUANTILES DECILES, Dk Son lo mismo que los centiles pero en este caso: k = 1, ..., 9 D1 C10 D 2 C 20 D 3 C 30 D 4 C 40 D 5 C 50 D 6 C 60 D 7 C 70 D8 C 80 D 9 C 90 CUARTILES, Qk Son lo mismo que los centiles pero en este caso: k = 1, ..., 3: Q1 C25 En resumen: Carmen Ximénez Q2 C50 Q3 C75 C10 ______________ D1 C20 ______________ D2 C25 _____________________________ Q1 C30 ______________ D3 C40 ______________ D4 C50 ______________ D5 ____________ Q2 C60 ______________ D6 C70 ______________ D7 C75 _____________________________ Q3 C80 ______________ D8 C90 ______________ D9 5 Análisis de Datos I Esquema del Tema 2 Ejemplo 7 (resuelto) Xi 1 2 3 4 5 ni 5 10 15 15 15 60 Pi 8 17 25 25 25 Pa 8 25 50 75 100 1. ¿Qué centil corresponde a la puntación 4? Solución: 4 = C75 2. Calcule el centil correspondiente a la puntación 2 Solución: 2 = C25 3. Calcule el centil 50 Solución: C50 = 3 4. Calcule el centil 25 Solución: C25 = 2 5. ¿Cuántos sujetos superan la puntuación 4? Solución: C75 = 4; Por tanto, la superan 15 sujetos (el 25%) 6. ¿Qué puntuación es superada por el 75% de sujetos? Solución: C25 = 2. Por tanto la puntuación X = 2 es superada por el 75% de los sujetos 7. ¿Cuántos sujetos hay entre los centiles 60 y 70? Solución: 6 sujetos (el 10%) 8. ¿Qué valores acotan el 50% central de sujetos? Solución: 2 y 4 C25 = 2 C75 = 4 25% C25 = 2 Carmen Ximénez 50% 25% C75 = 4 6 Análisis de Datos I Esquema del Tema 2 5. EJERCICIOS EJERCICIO 1 Con las puntuaciones de una muestra en un test de ansiedad (STAI) hemos construido la siguiente distribución de frecuencias. Xi 1 2 3 4 5 6 7 8 9 10 11 12 13 ni 2 4 5 9 22 12 6 6 6 3 2 2 1 na 2 6 11 20 42 54 60 66 72 75 77 79 80 pa 0,025 0,075 0,138 0,250 0,525 0,675 0,750 0,825 0,900 0,938 0,963 0,988 1,000 pi 0,025 0,050 0,063 0,113 0,275 0,150 0,075 0,075 0,075 0,038 0,025 0,025 0,013 1. ¿Cuál es el tamaño de la muestra? 2. ¿Cuál es el mayor valor observado? 3. ¿Cuál es el menor valor observado? 4. ¿Qué nivel de ansiedad es el más frecuente? 5. Si definimos como “ansioso grave” al que tiene 10 puntos o más, ¿cuántos de estos hay en la muestra? 6. ¿Con qué puntuaciones podemos extraer grupos extremos (25%)? 7. Represente gráficamente las frecuencias relativas y las acumuladas EJERCICIO 2 Xi 1 2 3 4 ni 5 3 7 5 na 5 8 15 20 pi 0,25 0,15 0,35 0,25 pa 0,25 0,40 0,75 1,00 k 25 40 75 99 1. ¿Qué centil corresponde a las puntuaciones 1 y 2? 2. ¿Qué centil corresponde a la puntación 3? 3. ¿Qué puntación corresponde al centil 25? 4. ¿Qué puntuación es superada por el 25% de sujetos? 5. ¿Cuántos sujetos hay entre los centiles 30 y 65? 6. ¿Qué valores acotan el 50% central de sujetos? EJERCICIO 3 Xi 1 2 3 4 5 6 7 8 9 10 11 12 13 ni 2 4 5 9 22 12 6 6 6 3 2 2 1 na 2 6 11 20 42 54 60 66 72 75 77 79 80 Carmen Ximénez Pi 2,50 5,00 6,25 11,25 27,50 15,00 7,50 7,50 7,50 3,75 2,50 2,50 1,25 Pa 2,50 7,50 13,75 25,00 52,50 67,50 75,00 82,50 90,00 93,75 96,25 98,75 100 1. Sistema de evaluación: 25% de suspensos 50% de aprobados 15% de notables 10% de sobresalientes ¿Qué notas delimitan cada categoría? 2. Si decidimos adoptar los siguientes criterios: Más de 5 para aprobado Más de 8 para notable Más de 11 para sobresaliente ¿Qué centil corresponde a cada puntuación? ¿Qué porcentaje de sujetos obtiene cada calificación? 7