kjiO ))) kjiO ))) r v v rv r r ∧+ =
Anuncio

Federico Stabach
Ingeniería Mecánica
UTN-FRBB
Mecánica del Sólido
Eje temático: Cinética de los sistemas materiales
Trabajo Práctico Final
Problema 1:
Para el sistema mostrado en la figura determinar la velocidad de un punto de la periferia del
disco utilizando primero el método absoluto y luego el método relativo.
Determinar además la energía cinética del disco.
Datos geométricos:
-
H=0,3m
r=0,1m
e=0.01m
ρ=8000kg/m3
ω1=4rad/s
ω2=3rad/s
Velocidad:
Método de movimiento absoluto:
) ) )
Tomaremos un sistema de referencia (O, i , j , k ) respecto del cual nos interesa referir el
movimiento del sólido. A esta terna la denominaremos “Terna absoluta”.
) ) )
Por otro lado adoptamos una terna móvil (O1 , i1 , j1 , k1 ) solidaria al sistema con respecto a
la cual conocemos las coordenadas del punto en análisis.
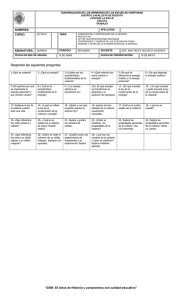
Ahora, aplicamos la forma impropia de la ley de distribución de velocidades que es:
r
r
v r
v P = vO1 + ω ∧ rO1P
1
Federico Stabach
Mecánica del Sólido
Ingeniería Mecánica
UTN-FRBB
v
Debemos tener en cuenta como condición para la aplicación de la forma impropia que vO1 debe
pertenecer al cuerpo en evaluación.
Ahora,
)
i
)
j
)
k
)
)
)
r r
r
vO1 = ω1 ∧ rO1 = 0
0
4 = −1,2i + 1,2 j + 0k
0,3 0,3 0,3
)
)
)
r r
r
ω = ω1 + ω 2 = 3i + 0 j + 4k
)
)
)
r
rO1P = 0i1 + r cos θj1 + rsenθk1
)
)
)
i
j
k
)
)
)
r r
ω ∧ rO1P = 3
0
4
= −0,4 cos θi − 0,3senθj + 0,3 cos θk
0 0,1 cos θ
0,1senθ
Entonces sólo queda sumar vectorialmente, así
) m
)
)
r
vP = [−(1,2 + 0,4 cos θ )i + (1,2 − 0,3senθ ) j + (0,3 cos θ ) k ]
s
Método de movimiento relativo:
Ahora analizaremos el movimiento del sólido respecto de una terna que se mueve respecto
de otra considerada fija y a la cual se desea referir el movimiento.
2
Federico Stabach
Mecánica del Sólido
Ingeniería Mecánica
UTN-FRBB
La terna fija se denomina absoluta y la móvil se denomina de arrastre. Aparecerá el vector
r
r
Ω que será el vector rotación absoluta de la terna móvil y v01 la velocidad de dicho punto también
absoluta.
Con esta configuración se conocerán entonces tres movimientos: Movimiento relativo,
movimiento de arrastre y movimiento absoluto.
Sabemos entonces que para nuestro caso será:
r r
r
r
r
r
r
r
r
r
v P = v rel + v arr , donde v rel = ω 2 ∧ rO1P y v arr = vO1 + Ω ∧ rO1P . Aplicando la forma impropia
r r
r r
r
r
podemos hallar vO1 = vO + ω1 ∧ rOO1 . Además sabemos que Ω = ω1 , entonces
r r
r r
r
r
r
v
v P = ω 2 ∧ rO1P + vO + ω1 ∧ rOO1 + ω1 ∧ rO1P
Ahora desmembramos la ecuación anterior para obtener el resultado buscado:
v
)
)
)
ω 2 = 3i´1 + 0 j1 + 0k1
)
)
)
r
rO1P = 0i´1 + r cos θj1 + rsenθk1
r
r
vO = 0
)
)
)
r
ω1 = 0i´1 + 0 j1 + 4k1
)
)
)
r
rOO1 = 0,3i´1 + 0,3 j1 + 0,3k1
Calculamos entonces los productos vectoriales
)
)
)
i1
j1
k1
)
)
)
r
r
0
0
= 0i´1 − 0,3senθj1 + 0,3 cos θk1
ω 2 ∧ rO1P = 3
0 0,1 cos θ 0,1senθ
)
)
)
i1
j1 k1
)
)
)
r r
0
4 = −1,2i´1 + 1,2 j1 + 0k1
ω1 ∧ rOO1 = 0
0,3 0,3 0,3
)
)
)
i1
j1
k1
)
)
)
r r
ω1 ∧ rO1P = 0
0
4
= −0,4 cos θi´1 + 0 j1 + 0k1
0 0,1 cos θ 0,1senθ
Ahora procedemos a realizar la suma vectorial obteniendo
) m
)
)
r
v P = [ − (1,2 + 0,4 cos θ )i1 + (1,2 − 0,3sen θ ) j1 + (0,3 cos θ ) k1 ]
s
Conclusión:
En cuanto al resultado, hemos obtenido el esperado, es decir que no importa el método
utilizado, el resultado será el mismo.
3
Federico Stabach
Ingeniería Mecánica
UTN-FRBB
Mecánica del Sólido
Cualquiera de los dos métodos es apropiado; se debe tener en cuenta cual de los dos
métodos es más conveniente aplicar de acuerdo a la configuración geométrica del problema y los
datos disponibles. Se puede apreciar además, la importancia de la elección más conveniente de
ubicación de las ternas.
Energía cinética:
La expresión general de la energía cinética para un sistema material establece:
e=
r r
1 2 1
r
mvO1 + Iωω O1ω 2 + mvO1 × ω ∧ rG
2
2
A los tres términos de la derecha los denominaremos e1, e2 y e3 respectivamente y los
iremos analizando por separado para luego ejecutar la suma total.
El primer miembro de la derecha e1 se denomina energía cinética de arrastre y es la que
tendría el sistema en el supuesto que toda la masa estuviera concentrada en el centro de reducción
siendo generada por este último.
En nuestro caso adoptaremos como centro de reducción el punto O1 coincidente con el
centro de masa del disco. Esta configuración es la más conveniente en nuestro caso y se justificará
mas adelante cuando evaluemos e3.
De los datos geométricos del problema podemos averiguar la masa del disco de la siguiente
forma:
ρ=
m
⇒ m = ρV = ρSe = ρπr 2 e = 8000π 0,12 0,01 ⇒ m = 2,51kg
V
)
)
)
r
m
Del apartado anterior sabemos que vO1 = (−1,2i + 1,2 j + 0k )m / s ⇒ vO1 = 1,7 ,
s
entonces, con estos valores, estamos en condiciones de hallar e1:
2
1 2
1
2 m
e1 = mvO1 = 2,51kg1,7 2
2
2
s
e1 = 3,61J
El segundo miembro de la ecuación de energía e2 =
1
Iωω O1ω 2 se denomina energía
2
cinética relativa y está originada por el movimiento relativo de cada punto respecto del centro de
reducción. En e2 aparece IωωO1 que resulta ser el momento de inercia del sólido respecto del eje ω
pasante por el centro de reducción y por otro lado aparece ω que simplemente es la suma de las
velocidades angulares que intervienen, es decir
r
r
r
)
)
)
)
)
)
)
)
)
ω = ω1 + ω 2 = 0i + 0 j + 4k + 3i + 0 j + 0k = (3i + 0 j + 4k )rad / s ⇒ ω = 5
rad
s
Pero concentrémonos ahora en la obtención del momento de inercia: Del Apéndice A.1.5 de
las Series de monografías docentes de Mecánica del sólido conocemos los momentos de inercia
para un disco circular delgado y lo ordenamos en una matriz:
4
Federico Stabach
Ingeniería Mecánica
UTN-FRBB
Mecánica del Sólido
I O1{i)1 }
1 2
2 mr
= 0
0
0
1 2
mr
4
0
0
0
0,013
)
0 ⇒ I O1{i1 } = 0
0,006
0 , pero nosotros debemos
0
0
0,006
1 2
mr
4
0
expresar el momento de inercia respecto de ω que pasa por O1. Para ello debemos realizar una
transformación lineal por rotación de ejes para lo cual utilizaremos la notación de Einstein que
establece: I ´´ij = cim c jn I ´mn , donde los cij son los cosenos directores que podemos determinar
haciendo un análisis geométrico de la figura siguiente:
)
k2
Como se ve, la figura representa el disco visto de perfil y en
base a ella podemos determinar que
tgϕ =
r
ω1
)
k1
ϕ
) r
O1 i1 ω 2
ω2 3
= ⇒ ϕ = 36,87° ,
ω1 4
entonces
los
cosenos
directores que interesan para nuestro caso serán:
c31 = 0,6
c32 = 0
c33 = 0,8
Y utilizando la notación de Einstein calculamos el
momento de inercia buscado haciendo:
2
2
2
Iωω O1 = I ´´33 = c31
I ´11 + c32
I ´22 + c33
I ´33
Iωω O1 = 0,009kgm 2
Entonces
1
1
1
Iωω O1ω 2 = 0,009kgm 2 5 2 2
2
2
s
e2 = 0,11J
e2 =
r
r
r
El tercer miembro de la ecuación de energía e3 = mvO1 × ω ∧ rG se denomina fuerza viva
compuesta y su valor depende del centro de reducción. Como se dijo antes se eligió como centro de
r
reducción el centro de masa G, de esta manera y como se puede apreciar en la expresión, rG se
anula, anulando el producto vectorial y luego todo el sumando. Por lo tanto en nuestro caso
particular obtenemos que:
r r
r r
r
r
e3 = mvO1 × ω ∧ rG = mvO1 × ω ∧ 0
e3 = 0
Entonces: e = e1 + e2 + e3 = (3,61 + 0,11 + 0) J
e = 3,72 J
5
Federico Stabach
Mecánica del Sólido
Ingeniería Mecánica
UTN-FRBB
Conclusión:
Como sabemos, el tensor de inercia representa la distribución de masa de un cuerpo
respecto de un sistema cordenado en función del tiempo. Lo que debemos lograr es expresar este
tensor de inercia de manera que no varíe con el tiempo eligiendo un sistema coordenado
conveniente.
En cuanto al centro de reducción adoptado, cabe mencionar lo acertado de haber elegido
como dicho punto al centro de masa del sistema simplificando de esta manera los cálculos en forma
sustancial.
Por Federico Stabach, UTN FRBB, Enero de 2005.
Bibliografía consultada:
Series de monografías docentes. Mecánica del Sólido. Dr. Ing. Liberto
Ercoli. GASM UTN FRBB Año 1998.
Material de apoyo:
Mecánica del Sólido. Prof. Ercoli. Apuntes tomados en clase. UTN FRBB
Año 2003.
Softwares utilizados:
Microsoft Word 2000
Microsoft Editor de Ecuaciones 3.0
MathCad Plus
AutoCad 2000
Microsoft Paint
6