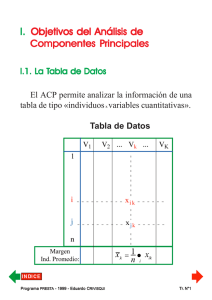
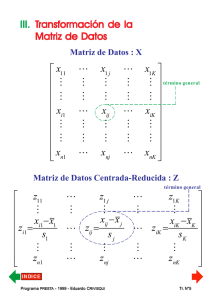
4. Importancia de la descripción de la forma de las nubes de puntos
Anuncio

4. Importancia de la descripción de la forma
de las nubes de puntos centradas en G
Teorema de Huygens
La inercia de una nube de puntos N(I) con respecto
a un punto m del espacio puede ser descompuesta en
la suma de la inercia de la nube de puntos N(I) con
respecto al Centro de Gravedad G L más la inercia del
Centro de Gravedad, munido de la masa total de la
nube de puntos, con respecto al punto m.
(demostración in E. CRIVISQUI "Análisis factorial de Correspondencias - un
instrumento de investigación en ciencias sociales", ULB-UCA, Asunción,
Paraguay, 1993)
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°52
5. El punto G de una nube de puntos-perfiles
es un punto característico del espacio
Por el teorema de Huygens:
I mΝ ( I ) = I GΝL( I ) + M tot d (2GL ,m )
Siendo :
mi > 0 ∀i ⇒ M tot > O
y
d (2i ,i' ) ≥ 0 ∀i ,i'
si GL ≡ m ⇒ d (2GL ,m ) = 0
si GL ≠ m ⇒ d (2GL ,m ) > 0
y
si GL ≠ m ⇒ I mΝ ( I ) > I GΝL( I )
en cambio,
si GL ≡ m ⇒ I mΝ ( I ) = I GΝL( I )
puesto que, si...
d
2
(GL ,m )
= 0 ⇒ M tot d (2GL ,m ) = 0
La inercia, con respecto al Centro de Gravedad, del sistema
de masas de los puntos-perfiles constituye un valor mínimo.
Interés de esta conclusión...
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°53
6. Reducción de una nube de puntos-perfiles
al Centro de Gravedad
Puesto que :
I GΝ' L( I ) = I GΝL( I ) + M tot d (2GL ,G'L )
La inercia de N(I) con respecto a G’L puede formularse :
I GΝ' L( I ) = I //ΝG( LI ) + I //ΝG( LI ) + I //ΝG( IL ) + M tot d (2GL ,G'L )
∆
Ε⊥∆
Β⊥Ε⊥∆
La recta que pasa por el Centro de Gravedad es la
recta que minimiza la suma de los cuadrados de los
desvíos de los puntos de la nube medidos ortogonalmente a la dirección de la recta.
Todas estas propiedades pueden ser
generalizadas al caso de espacios de
más de tres dimensiones.
La descomposición de la inercia necesita
que el nuevo referencial sea :
✔
ortogonal
✔
centrado en el Centro de Gravedad de
la nube de puntos
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°54
I. DEFINICIÓN DE UN NUEVO REFERENCIAL DE REPRESENTACIÓN DE UNA
TABLA DE CONTINGENCIA
1. ¿Cómo hacer para construir un sistema de
ejes ortogonales...?
✔
¿Cuál es el interés de construir un nuevo referencial...?
Sea una Tabla T
La nube de puntos-columna N(J) = Q{J1, J2, J3, J4, J5}
Referencial tres modalidadesen línea : {L1 , L2, L3}
En ese espacio, creamos un nuevo referencial centrado y
ortogonal (por construcción).
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°55
2. Referencial ortogonal y centrado en GJ
Los puntos-perfiles J"1, J"2, J"3, J"4 y J"5 son determinados
por la proyección ortogonal de los puntos J1, J2, J3, J4 y J5 sobre
el eje I.
✔
¿Cuál es la inercia de la nube de puntos-perfiles
a lo largo del eje I...?
✔
¿Cuál es la inercia residual de la nube de puntosperfiles ...?
Para representar las distancias de todos los puntos con
respecto a GJ , podemos representar —en todos los subespacios de dos dimensiones— las proyecciones de la nube de
puntos sobre los ejes del nuevo referencial.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°56
Primer subespacio de una dimensión
Segundo subespacio de dos dimensiones
La ortogonalidad de los ejes permite presentar la inercia de
la nube con respecto a G en una sucesión de gráficos de los subespacios de una o dos dimensiones.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°57
El nuevo tipo de referencial presenta tres
ventajas importantes :
✔ Permite el análisis completo de la forma de la nube de
puntos-perfiles;
✔ Permite la representación de la forma de la nube de puntosperfiles cualquiera sean las dimensiones de las nubes de
puntos.
✔ Permite producir la representación objetiva de esas nubes
de puntos, es decir «estables», independientes de la opción
(«punto de vista») del analista.
Es posible asociar a esas representaciones gráficas los coeficientes de control que constituyen la componente digital
complementaria de ese modo analógico de comunicar el
sentido de la información aportada por la Tabla de Contingencia.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°58
3. ¿Cómo construir una «buena» representación de la información de la Tabla T...?
¿Cómo elegir el «mejor» sistema de ejes que sirva de referencial de representación de la Tabla T...?
Direcciones principales de las nubes de puntos-perfiles
Plano α en un gráfico de dos dimensiones
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°59
4. ¿Cómo elegir entre esos dos sistemas de
ejes igualmente posibles...?
➩
¿Cuál sistema de ejes aporta la «mejor» representación de la
dispersión de la nube de puntos en torno a G...?
✔ Criterio de selección...
El mejor referencial es aquel para el cual las proyecciones
de los puntos-perfiles sobre un eje son las más grandes, de
manera tal que los desvíos de la nube de puntos-perfiles —
medidos ortogonalmente con respecto al eje— sean los más
pequeños.
Para obtener, por proyección ortogonal, la mejor imagen
posible de una nube de puntos-perfiles es necesario :
- proyectar los puntos de la nube sobre una recta que
maximice la inercia proyectada de la nube a lo largo de
ella.
o bien,
- proyectar la nube a lo largo de una recta con respecto a
la cual la inercia residual ortogonal de la nube de puntosperfiles es mínima.
✔ «Direcciones principales de deformación»
La recta que responde a esa exigencia es llamada «dirección
principal de deformación» de la nube de puntos-perfiles.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°60