Document
Anuncio

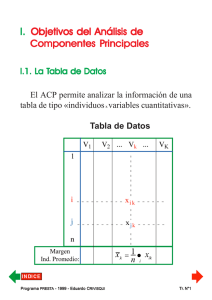
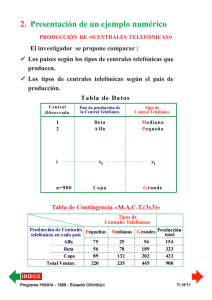
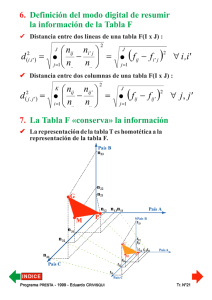
III. Transformación de la Matriz de Datos Matriz de Datos : X x11 M M x i1 M M x n1 L M M L M M L x1 j M M xij M M xnj L M M L M M L x1K M término general M xiK M M xnK Matriz de Datos Centrada-Reducida : Z L z11 z1 j M M M xij − x j xi1 − x1 z = L zij = i1 s1 sj M M M L z n1 znj Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI término general z1K M xiK − xK L ziK = sK M M L znK L M Tr. N°5 ✔ Efectos de esa tranformación de la Matriz de Datos § Centrando la Matriz de Datos... - no se modifica la evaluación de la distancia entre dos individuos cualesquiera de la tabla. - no se modifica la evaluación de la correlación entre dos variables cualesquiera de la tabla. § La reducción de la Matriz de Datos... - no modifica la evaluación de la relación entre dos variables cualesquiera de la tabla. - hace que la evaluación de la semejanza entre dos individuos cualesquiera de la tabla sea independiente de las escalas de medida de las variables. Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°6 IV IV.. La nube de puntos-individuos en R3 y en Rk § La base (e1,e2,e3) es una base ortonormal, centrada en G. r § A la variable x1 le corresponde el eje engendrado por e1 = (1,0,0), y así siguiendo... Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°7 ✔ En R3 el individuo i queda representado por : § El punto i , de coordenadas : xi − x xi − x xi − x 1 1 , 2 2 , 3 3 sx sx sx 1 2 3 Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°8 § El extremo del vector wi , combinación lineal de los vectores de la base ortonormal, xi 3 − x3 wi1 xi1 − x1 xi 2 − x2 .e = w .e + .e + wi = s x 1 s x 2 sx 3 i 2 1 2 3 wi 3 IV IV.. 1. Origen del espacio § El origen del espacio representa el «individuo medio». § El punto 0, en el espacio original, es el extremo del «vector de medias» de todas las variables. Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°9 IV IV.. 2. Inercia total de la nube de puntos-individuos § Considerando el individuo i en Rk dispersión de NGI = Inercia total de N 0I = ∑d (i ,0 ) n i=1 K x −x Siendo : d (i ,0 ) =∑ ik k k =1 sk I NI 0 1 n 2 2 § Si representamos al individuo i por un punto en el espacio R 3 2 I NI 0 n x − x 3 xik − xk 1 = ∑ ∑ = ∑ ∑ ik k n i =1 k =1 sxk k =1 n i =1 sxk 1 3 =∑ n 3 1 s 2 k =1 x k 3 =∑ 2 1 s2 k =1 x k (n ∑ (x n 1 i =1 ik − xk ) 2 ) (s ) = k = 3 2 xk Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°10 § Si representamos al individuo i como el extremo del vector wi I NI 0 siendo w i I NI 0 n = ∑ wi n i =1 1 2 2 xik − xk = ∑ sxk k =1 2 3 = Tr (V ) = k ... de modo que, en R3 I NI 0 = Tr (V ) = 3 ¿Cómo se define la matriz V ...? V...? Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°11 IV IV.. 3. La matriz de inercia de la nube de puntos-individuos § D : métrica de los pesos en Rn 1 0 0 n O 1 0 D(n×n) = 0 n O 1 0 0 n § Z : matriz X centrada-reducida M M xij − x j L L L = L L L Z ( ) sx j M M nxk Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°12 § V : matriz de inercia, es la matriz de correlaciones V = Z' D Z 1 M V = rx j x1 M r x K x1 L rx1x j O M L 1 M M L rxK x j Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI L rx1xK M M L rx j xK O M L 1 Tr. N°13 IV IV.. 4. Contribución a la inercia del individuo i 1 w2 i n Contr. I0 (i ) = × 100 I0 IV togonal de la nube de IV.. 5. Proyección or ortogonal puntos sobre un eje § Proyectando ortogonalmente los n puntos de la nube NI sobre el primer eje... n 1 2 1 Î = ∑ ŵi n i =1 1 0 2 n x − x 1 = ∑ i1 1 = 1 = sx2r n i =1 sx1 1 § Si las variables son sólo centradas : n 1 1 2 1 Î 0 = ∑ ŵi n i =1 n 2 1 = ∑ [xi1 − x1] = sx2c n i =1 1 ... igualmente para la proyección sobre el segundo eje, el tercer eje, etc. Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°14 IV togonal de la nube de IV.. 6. Proyección or ortogonal puntos sobre el plano definido por los dos primeros ejes n 1 Î = ∑ ŵ1i ,2 n i =1 2 1 0 n x − x xi2 − x2 i1 1 1 Î = ∑ + n i =1 sx1 sx2 2 1 0 Î 10 = 1 + 1 = 2 2 s r x1 2 s r x2 § Si las variables son sólo centradas : n 1,2 2 1 1 Î 0 = ∑ ŵi n i =1 n 2 1 1 Î 0 = ∑ [(xi1 − x1 ) + (xi2 − x2 )] n i =1 Î 10 = sx2c + sx2c 1 2 Inercia proyectada ⇒ suma de varianzas ⇒ «dispersión» Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°15