Document
Anuncio

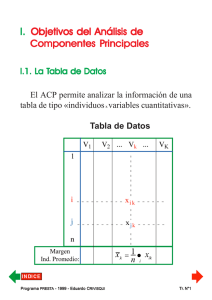
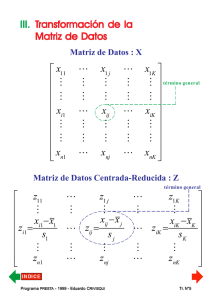
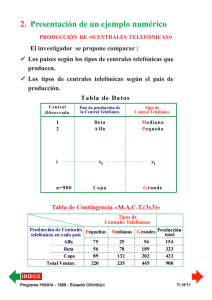
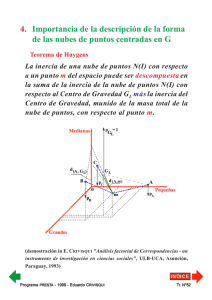
5. Proceso de construcción del nuevo referencial La definición del nuevo referencial se hace en cuatro etapas: ➩ Primera etapa : Búsqueda de la primera dirección principal de la nube de puntos-perfiles N(I) o N(J). Por ej.: recta p1, ➩ Segunda etapa : Definición del subespacio de J-1 dimensiones, ortogonal la primera dirección principal elegida (inercia residual ortogonal de la nube de puntos), ➩ Tercera etapa : Búsqueda, en ese subespacio, de la segunda dirección principal de deformación. Por ej.: recta p2, ➩ Cuarta etapa : Se repiten las etapas 1°, 2° y 3° hasta anulación de la inercia residual a proyectar en un último subespacio ortogonal. Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°61 La inercia IG de las nubes de puntos-perfiles N(I) y N(J) es así descompuesta en : I G = I //N0( I ) + I //N0( I ) + ... + I //N0( I ) δ1 δ2 δI I G = I //N0( J ) + I //N0( J ) + ... + I //N0( J ) δ1 δ2 puesto que : δJ I G = I GΝL( I ) = I GΝC( J ) , además... I //N0( I ) ≥ I //N0( I ) ≥ ... ≥ I //N0( I ) δ1 δ2 δI I //N0( J ) ≥ I //N0( J ) ≥ ... ≥ I //N0( J ) δ1 δ2 δJ por definición de las «direcciones principales de deformación» de las nubes de puntos-perfiles. ¿Cuántas direcciones principales se pueden extraer (como máximo) para descomponer completamente la inercia de una nube de puntos-perfiles...? Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°62 ➩ Para hacer la «mejor» representación posible de la inercia IG de una nube de puntos-perfiles es necesario y suficiente: ✔ determinar las p direcciones principales de deformación de la nube, ✔ construir las p rectas que pasan por G y que son colineales con esas direcciones principales, ✔ proyectar los puntos ortogonalmente a esas rectas, construyendo así los p ejes factoriales, ✔ representar sucesivamente los planos factoriales que resultan de la descomposición de la inercia IG de la nube de puntos-perfiles... Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°63 6. ¿Cómo se calculan las rectas que constituyen el nuevo referencial...? ➩ Direcciones principales de N(I) : «diagonalización de la matriz de inercia». Problema clásico del cálculo numérico... Determinación de los valores propios y los vectores propios asociados a una matriz simétrica, definida positiva. ➩ De ese proceso de cálculo, resultan los vectores propios uα de V(J, J) y wα de B(I, I) , asociados a los mismos valores propios ➩ 0 ≤ λ α ≤ 1. Los vectores propios están ligados por las siguientes relaciones : 1 = uα K'.wα λα y 1 = wα K .uα λα Se diagonaliza la matriz de inercia correspondiente al espacio que contenga menos puntos. Los vectores propios del otro espacio son definidos por medio de las relaciones anteriores. ➩ ¿Cómo se contruyen los ejes factoriales? Por proyección ortogonal de los puntos sobre las direcciones principales de las nubes de puntos-perfiles. Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°64 J. REPRESENTACIÓN FACTORIAL DE LA INFORMACIÓN APORTADA POR UNA TABLA DE CONTINGENCIA 1. Propiedades de los factores de una nube de puntos-perfiles a) Coordenadas de los puntos-perfiles Fα (i ) = ∑ zij uαj J Gα ( j ) = ∑ kij wαi I y j =1 i =1 b) Coordenadas del Centro de Gravedad Las coordenadas del Centro de Gravedad en los espacios factoriales son todas nulas. I ∀i ∈ I ; ∀α ,∑ fi . Fα (GL ) = 0 i =1 J ∀j ∈ J ; ∀α , ∑ f . j Gα (GC ) = 0 j =1 ➩ Los factores son p variables «centradas» (continuas, a valor en R). Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°65 c) Varianza de los factores = 0, de modo que : ∀α = 1,..., p Sabemos que : xα , s = ∑ pi (xαi − xα ) = ∑ pi (Fα (i ) − 0) 2 α I I 2 i =1 2 i =1 s = ∑ pi (Fα (i )) = λ α 2 α I 2 i =1 ➩ Varianza del factor α : inercia de N(I) a lo largo del eje. ➩ Inercia a lo largo de un eje α : valor propio del eje α... I λ α = ∑ pi (Fα (i )) 2 i =1 ∀α = 1, 2 ,..., p d) Significado de los valores propios de una matriz de inercia ➩ Valor propio asociado a un eje factorial : parte asumida por el eje de la relación observada entre las variables de la Tabla T. e) ¿Qué significa un valor propio λα = 1...? Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°66 f) ¿Cuáles son los valores propios (y los ejes factoriales) pertinentes de un análisis...? g) Tasa de inercia de un factor λα λα τα = × 100 = × 100 IG ∑ λα α p de modo que: ∑ τα = 100% α =1 h) Tasa de inercia de un plano factorial τα λ ( = αj + λαk ∑ λα ) × 100 α ¿Qué significa la tasa de inercia de un eje factorial ...? i) La representación factorial de las nubes de puntos N(I) y N(J) conserva la información de la tabla T Verificación que aconsejamos realizar... d 2 (i ,i' ) fij f i' j 1 =∑ − fi'. j =1 f . j f i . K 2 y d 2 (i ,i' ) p = ∑ (Fα (i ) − Fα (i' )) 2 α =1 Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°67 2. Componentes digitales del mensaje a) Contribución de los puntos-perfiles a la inercia a lo largo de un eje factorial pi (Fα (i )) CTR α (i ) = λα 2 × 100 p j (Gα ( j )) CTR α ( j ) = λα 2 ➩ × 100 ∀i ∈ N (I ) ∀j ∈ N (J ) El coeficiente CTRα(i) (o CTRα(j)) es llamado «contribución del punto-perfil» a la inercia del eje α. Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°68 b) Calidad de representación de un punto-perfil a lo largo de un eje factorial ➩ Distancia de un punto-perfil al origen : d d 2 (i ,G ) 2 ( j ,G ) p = ∑ (Fα (i )) ∀i ∈ N (I ) 2 α =1 p = ∑ (Gα ( j )) ∀j ∈ N (J ) 2 α =1 De modo que : 2 ( Fα (i )) ∀α = 1, ..., p COR α (i ) = × 100 2 d (i ,G ) ( Gα ( j )) COR α ( j ) = 2 2 ➩ d ( j ,G ) × 100 ∀α = 1, ..., p Siendo : p ∑ COR α (i ) = 1 ∀i ∈ N (I ) α =1 p ∑ COR α ( j ) = 1 ∀j ∈ N (J ) α =1 ➩ El coeficiente CORα(i) (CORα(j)) es designado también : COS2α(i) (COS2α(j)). Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°69 c) Significado del coeficiente de calidad de representación de un punto-perfil sobre un eje factorial ➩ El cuadrado del coseno del ángulo w mide la «calidad de la representación» de la distancia del punto i al origen del eje α α. ( Fα (i )) ( )= cos (ω) = COR α i 2 ➩ 2 d (2i ,G ) ¿Qué significa «medir la calidad de representación de un punto-perfil» sobre un eje factorial...? 2 ( ( ) ) F i ' cos 2 (ω' ) = COR α (i' ) = α 2 d (i' ,G ) Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°70 d) Significado del coeficiente de calidad de representación de un punto-perfil sobre un plano factorial Vemos que: d (2i' ,0 ) = (F12 (i ) + F22 (i )) la «calidad de representación» sobre el plano factorial : ( F (i ) + F (i )) (i ) = 2 COR β ➩ 2 2 1 d (2i ,0 ) Otro ejemplo de control de errores de proyección : Pr ograma PREST do CRIVISQ A - 1999 - Eduar UI Programa Eduardo PRESTA RIVISQUI Tr. N°71