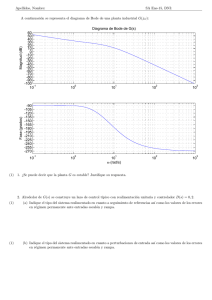
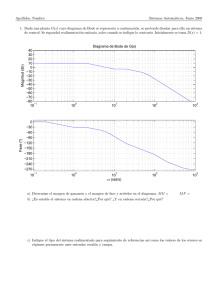
UNIVERSIDAD NACIONAL DE ASUNCI´ON Facultad de Ingenierıa

UNIVERSIDAD NACIONAL DE ASUNCIÓN
Facultad de Ingenierı́a
Ingenierı́a Electrónica
DISEÑO E IMPLEMENTACIÓN DE UN SISTEMA DIGITAL BASADO
EN FPGA DE LA TÉCNICA HARDWARE IN THE LOOP APLICADO A
UN MOTOR ASÍNCRONO TRIFÁSICO
Guido José Valenzano Tocaimasa
Asesores:
Prof. Dr. Raúl Gregor
M.Sc. Ing. José Rodrı́guez
Prof. Ing. Miguel Benı́tez
San Lorenzo, Paraguay
Noviembre de 2013
RESUMEN EJECUTIVO
1
Diseño e implementación de un sistema digital basado en FPGA de la
técnica Hardware in the Loop aplicado a un motor ası́ncrono trifásico
Guido Valenzano, Estudiante.
Raúl Gregor, José Piñeiro, Miguel Benı́tez, Orientadores.
Ingenierı́a Electrónica.
Departamento de Sistemas de Potencia y Control.
Facultad de Ingenierı́a, Universidad Nacional de Asunción.
Resumen—El presente Trabajo Final de Grado (TFG) presenta
el diseño de una plataforma Hardware in the Loop que verifica el
comportamiento de un motor ası́ncrono trifásico y se implementa
en un dispositivo Field-Programmable Gate Array (FPGA). El
diseño de esta plataforma incluye el modelado matemático del
motor ası́ncrono trifásico, diseño de la unidad de procesamiento,
elección de la arquitectura de computador, diseño del juego de
instrucciones, consideraciones de temporización y diseño de los
módulos de entrada/salida. La plataforma se valida, implementando el diseño en una placa de evaluación y comparando los
resultados obtenidos con simulaciones por computadora.
Palabras claves—FPGA, Hardware in the Loop, motor,
máquina ası́ncrona trifásica.
Abstract—This Final Grade Work presents the development
of a Hardware in the Loop platform which emulates the dynamic behaviour of a three-phase asynchronous machine and
is implemented on a Field-Programmable Gate Array (FPGA).
The design of the platform includes the mathematical model of
the three-phase asynchronous machine, design of the processing
unit, selection of computer architecture, design of the instruction
set, timing constraints and design of input/output modules.
The platform is validated with the implementation over an
evaluation board and comparing the results obtained with the
ones performed in computer simulations.
Index Terms— FPGA, Hardware in the Loop, motor, threephase asynchronous machine.
I. I NTRODUCCI ÓN
En los últimos años, el diseño de controladores se ha
visto favorecido por la aparición y uso de herramientas
computacionales para realizar simulaciones de prototipos. El
empleo de este tipo de prácticas permite disminuir los tiempos
de prototipado; sin embargo, el proceso de diseño exige
la implementación real del controlador y su prueba para
detectar posibles errores relacionados con consideraciones o
simplificaciones, imperfecciones en el proceso de fabricación,
o cuestiones relacionadas con la seguridad. Estos inconveG. Valenzano es investigador en el Departamento de Sistemas de Potencia y
Control de la Facultad de Ingenierı́a de la Universidad Nacional de Asunción.
R. Gregor es Docente Investigador de Tiempo Completo y Dedicación
Exclusiva (DITCoDE) y Jefe del Departamento de Sistemas de Potencia
y Control, desempeñando ambos roles en la Facultad de Ingenierı́a de la
Universidad Nacional de Asunción.
J. Rodrı́guez es investigador en el Departamento de Electrónica e Sistemas
de la Universidade de A Coruña.
M. Benı́tez es Jefe de las Cátedras de Sistemas Digitales I y II impartidos
en la Facultad de Ingenierı́a de la Universidad Nacional de Asunción.
nientes difı́cilmente pueden ser observados o previstos en las
simulaciones.
Dentro de la infinidad de procesos sujetos a control, existen
algunos que no pueden mantenerse inactivos por mucho tiempo, que podrı́an resultar riesgosos para realizar procedimientos
experimentales, o que resultan inviables para pruebas de
laboratorio. Por ejemplo: la generación de energı́a eléctrica,
el latir del corazón humano, sistemas de control en vehı́culos,
entre otros. En estos casos es donde resulta valiosa la técnica
Hardware in the Loop, que consiste en realizar simulaciones
con componentes reales en conexión con componentes simulados en tiempo real. Usualmente, el software y hardware
del sistema de control corresponden al sistema real; mientras
que el proceso controlado, consistente en actuadores, procesos
fı́sicos y sensores pueden ser simulados total o parcialmente
[1]. La representación esquemática de esta técnica puede
observarse en la Figura 1.
La técnica Hardware in the Loop ha encontrado aceptación
y crecimiento sostenido en diferentes ramas de la ingenierı́a
y en investigaciones multidisciplinarias. Prueba de ello, son
publicaciones sobre diseño de vehı́culos terrestre y aéreos [2]–
[10], máquinas eléctricas y sistemas de potencia [11]–[15],
aplicaciones médicas [16]–[19], y áreas diversas [20]–[24].
Asumiendo que la precisión lograda en las simulaciones con
la técnica Hardware in the Loop depende de la complejidad
del modelo matemático implementado en la banca de prueba;
resulta evidente la necesidad de recurrir a sistemas digitales
capaces de: otorgar la flexibilidad suficiente para modelar el
proceso y procesar a una velocidad elevada (tiempo real),
de modo a utilizar modelos de cierta complejidad. Tradicionalmente, se han utilizado computadoras convencionales,
microcontroladores de última generación, dispositivos de procesamiento digital de señales (DSP, por sus siglas en inglés),
y dispositivos FPGA (Field Programmable Gate Array). En
la actualidad, la mayorı́a de las investigaciones relacionadas
con la técnica Hardware in the Loop han utilizado dispositivos
FPGA como soporte de hardware [25]–[27].
Por los motivos mencionados anteriormente, y a modo de
Figura 1.
Diagrama de bloques de la técnica Hardware in the Loop.
RESUMEN EJECUTIVO
evaluar experimentalmente la técnica denominada Hardware in
the Loop, en el marco de este trabajo, se pretende implementar
un sistema digital basado en FPGA capaz de reproducir el
comportamiento dinámico de un motor ası́ncrono trifásico, resolviendo las ecuaciones que componen el modelo matemático
del mismo.
El presente documento se organiza de la siguiente manera:
en la sección II se introduce el modelado matemático de la
máquina ası́ncrona trifásica. En la sección III se presentan
las herramientas de hardware y software utilizadas en el
diseño. Posteriormente, se presentan las consideraciones de
diseño e implementación de las distintas unidades funcionales:
unidad de procesamiento (sección IV), unidad de memoria
y contador de programa (sección V), juego de instrucciones
(sección VI), módulo de reloj (sección VII), módulo de salida
(sección VIII), módulo de entrada (sección IX) y unidad de
control (sección X). Luego, en la sección XI se resume la etapa
de diseño y se presenta una perspectiva global del sistema
digital. Posteriormente, en la sección XII se describen las
simulaciones realizadas y presentan los resultados. Finalmente,
en la sección XIII se sintetizan las conclusiones más relevantes
y futuras lı́neas de investigación a partir de este trabajo.
II. M ODELADO MATEM ÁTICO
El modelo matemático del motor ası́ncrono trifásico se encuentra desarrollado en los apartados siguientes. En el apartado
II-A, se presentan las definiciones y supuestos que son tenidos
en cuenta, mientras que en el apartado II-B se detallan las
ecuaciones matemáticas que modelan el sistema. La deducción
de las ecuaciones que se presentan en el apartado II-B pueden
encontrarse en los trabajos de diferentes autores [28]–[30] con
distintos grados de profundidad. En este resumen, sólo las
ecuaciones y relaciones más importantes se tienen en cuenta.
2
Figura 2.
Representación gráfica de un motor ası́crono trifásico.
La sección transversal de una máquina ası́ncrona trifásica
que cumple con éstas condiciones puede verse en la Figura 2.
En general, el subı́ndice s denota variables referidas al estátor,
mientras que las variables referidas al rotor se simbolizan con
el subı́ndice r. Asimismo, las inductancias, corrientes, tensiones y flujo magnético se individualizan en función al eje —a, b
o c— en cuestión. Además de las variables electromagnéticas,
aparecen también en la Figura 2 la posición relativa del rotor
respecto al estátor θr y la velocidad del rotor ωr .
B. Ecuaciones en tiempo continuo y discreto
Las ecuaciones que modelan el comportamiento dinámico
de la máquina ası́ncrona trifásica a nivel electromagnético
pueden escribirse utilizando la representación en espacio de
estados como:
ẋ(t) = A(t)x(t) + Bu(t) .
A. Definiciones y notación
Ciertas definiciones, asunciones y simplificaciones son
necesarias para describir el comportamiento de un motor
ası́ncrono. Éstas, son homogéneas a lo largo de la literatura
[31]–[33] y pueden ser resumidas en los siguientes puntos:
El estátor tiene n inductores idénticos, repartidos uniformemente de manera a formar un sistema n-fásico
balanceado, en estrella y con el neutro aislado. En el
presente trabajo se asume n = 3.
El rotor cuenta con un número idéntico de fases y polos
que el estátor. Si el rotor es de jaula de ardilla, en vez
de bobinas se tienen barras de cobre o aluminio que se
encuentran cortocircuitadas.
La distribución espacial de las fuerzas magnetomotrices
y del flujo en el entrehierro son sinusoidales. Es decir,
se considera únicamente la frecuencia fundamental de la
onda de inducción del entrehierro.
El estátor y el rotor están compuestos por un material
magnético de permeabilidad infinita, por lo que el flujo
magnético se concentra en el entrehierro.
Se desprecia el efecto de las ranuras, considerándose
constante y de espesor despreciable el entrehierro.
Se desprecian los fenómenos de histéresis y saturación,
y en consecuencia las pérdidas magnéticas.
Se ignora el efecto de la temperatura en los materiales.
(1)
T
donde el vector de estado x(t) = [iαs , iβs , iαr , iβr ] , el
vector de entrada u(t) = [uαs , uβs , 0, 0] y las matrices A(t)
y B se definen como:


−c2 Rs
c 3 ωr L M
c 3 Rr
c 3 ωr Lr
−c3 ωr LM
−c2 Rs
−c3 ωr Lr
c 3 Rr 
 ,
A(t) = 
 c 3 Rs
−c4 ωr LM
−c4 Rr
−c4 ωr Lr 
c 4 ωr L M
c 3 Rs
c 4 ωr L r
−c4 Rr
(2)


c2
0
−c3
0
 0

c
0
−c
2
3
B=
.
(3)
−c3
0
c4
0 
0
−c3
0
c4
Asimismo, Rs y Rr son las resistencias de estátor y rotor,
ωr es la velocidad angular del rotor, Ls = Lls + LM , Lr =
Llr + LM son las inductancias del estátor y rotor, y LM es
la inductancia de magnetización. Además, las constantes ci
(i = 1, 2, 3, 4) son definidas como:
LM
Ls
Lr
, c3 =
, c4 =
.
(4)
c1
c1
c1
El modelo de (1) puede llevarse al espacio discreto utilizando el método de Euler. Luego, la predicción de la siguiente
muestra x̂(k + 1) puede expresarse como:
c1 = Ls Lr − L2M , c2 =
x̂(k + 1) = [I + Tm A(k)]x(k) + Tm Bu(k) ,
(5)
RESUMEN EJECUTIVO
3
Figura 3. Representación en forma de sistema del modelo matemático del
motor ası́ncrono trifásico.
donde k representa a valores correspondiente la muestra actual,
Tm el perı́odo de muestreo, e I es la matriz identidad.
Para una máquina con P polos, la dinámica mecánica está
dada por las siguientes ecuaciones:
P
(ψβr iαr − ψαr iβr ) ,
(6)
2
P
d
(7)
Ji ωr + Bi ωr = (Te − TL ) ,
dt
2
donde TL denota el par de carga, Ji el coeficiente de inercia,
ψαβr el flujo del rotor y Bi el coeficiente de fricción viscosa.
Mediante un procedimiento análogo al empleado para hallar
la ecuación (5), se pueden llevar al espacio discreto las
ecuaciones (6) y (7). Definiendo las variables:
Figura 4. Placa de evaluación SP605 de Xilinx. Se resalta con un recuadro
rojo el dispositivo FPGA.
Te = 3
Bi
,
Aω = −
Ji
P
Bω =
,
2Ji
uω = T e − T L ,
3P
[x2 (k)x3 (k) + x1 (k)x4 (k)] ,
4
ω̂r (k + 1) = [1 + Tm Aω (k)] ωr (k) + Tm Bω uω (k) .
Diagrama de la unidad de procesamiento mı́nimo propuesto.
(8)
y haciendo uso de las variables de estado xi (i = 1, 2, 3, 4), las
ecuaciones mecánicas en tiempo discreto se expresan como:
Te (k) =
Figura 5.
subsistemas fueron descritos en el lenguaje VHDL utilizado el
entorno de desarrollo ISE [38] de Xilinx, y simulados mediante
el simulador integrado ISim [39].
(9)
IV. D ISE ÑO DE LA UNIDAD DE PROCESAMIENTO
(10)
La Figura 3 muestra un sistema que modela las ecuaciones
(5), (9) y (10). Las variables de entrada son las tensiones sobre
los bobinados del estátor va , vb , vc , y el par de la carga TL .
La salida del sistema puede ser cualquier parámetro obtenido
a través de operaciones matemáticas sobre las entradas o
variables de estado, siendo las más utilizadas en aplicaciones
de control: el par eléctrico Te , la velocidad del rotor ωr ,
las corrientes del estátor iαs , iβs y las corrientes del rotor
iαr , iβr .
III. R ESTRICCIONES DE HARDWARE Y SOFTWARE
En el marco del presente trabajo, se ha utilizado una placa
de evaluación SP605 del fabricante Xilinx, propiedad del
Departamento de Sistemas de Potencia y Control de la Facultad de Ingenierı́a de la Universidad Nacional de Asunción.
La misma incorpora un FPGA Spartan-6 XC6SLX45T, que
corresponde a una familia entry-level de última generación
[34]; el dispositivo FPGA puede verse señalado en la Figura 4.
La placa SP605 cuenta con una serie de caracterı́sticas y
periféricos [35] que la hacen ✭✭ideal para diseños de bajo
costo y comunicaciones✮✮ [36, p. 5]. Asimismo, se cuenta con
la placa adicional FPGA Mezzanine Card XM105 [37] que
amplı́a el número de pines de entrada/salida y periféricos de
la SP605. Algunas consideraciones de diseño realizadas en
las secciones siguientes, se realizaron a partir del hardware
mencionado. En cuanto al software, los bloques funcionales y
Para el diseño de la unidad de procesamiento, se realizan
algunas consideraciones que derivan en el modelo propuesto.
En el apartado IV-A se analizan las operaciones aritméticas
necesarias para los cálculos del modelo matemático, en el
apartado IV-B se presentan las alternativas de representación
de números reales, ası́ como ventajas y desventajas de cada
una de ellas, y en el apartado IV-C se detalla la unidad de
procesamiento implementada en este trabajo.
A. Análisis de operaciones
Teniendo en cuenta la posterior implementación del diseño
digital sobre un dispositivo FPGA, conviene realizar algunas
simplificaciones en las operaciones matemáticas. En efecto,
una inspección minuciosa de las ecuaciones (5), (9) y (10),
permiten concluir que si:
1. Cada división a realizarse, puede obtenerse multiplicando un número por la inversa del otro,
2. El signo de cada operando puede cambiarse arbitrariamente,
entonces, las operaciones necesarias para los cálculos se reducen a sumas y productos de números reales. Como resultado,
se propone una unidad de procesamiento mı́nimo similar a la
Figura 5, donde a y b son los operandos de entrada, neg(a)
y neg(b) son señales que permiten alterar el signo de a y
b respectivamente, op es el selector de operación, e y es el
resultado.
RESUMEN EJECUTIVO
4
B. Representación de números reales
Al momento de implementar la unidad de procesamiento
mı́nimo de la Figura 5 en un dispositivo FPGA, resulta
imperativo definir el método de representación y aritmética de
números reales. Existen dos alternativas: la primera de ellas
es la representación en punto flotante, con
x ≈ (−1)s × m × be ,
(11)
donde el número real x se aproxima mediante un bit de
signo s, un significando m, una base de exponenciación b
y un exponente e; por otro lado, la segunda alternativa es la
representación en punto fijo, con
x ≈ (−1)s × (p + q) ,
(12)
donde el número real x se aproxima mediante un bit de signo
s, una parte entera p y una parte fraccionaria q. Cada uno
de éstos métodos de representación cuentan con ventajas y
desventajas, relacionadas con aspectos de rango numérico,
velocidad de ejecución de operaciones, consumo de recursos,
estandarización, y soporte por parte de fabricantes.
C. Unidad de procesamiento propuesta
Teniendo en cuenta las consideraciones planteadas en las
secciones anteriores, se propone en este trabajo una unidad de
procesamiento, similar a la Figura 5, donde se representan los
datos utilizando números de punto flotante de precisión simple.
Los bloques que implementan la suma y multiplicación de
números reales, son propiedad intelectual del fabricante Xilinx,
y se encuentran documentados en [40].
Estas elecciones se fundamentan en el amplio rango
dinámico que ofrece la representación de punto flotante, ası́
como la facilidad que otorga para contrastar resultados experimentales con simulaciones hechas por computadora. De igual
manera, se utilizaron los bloques de propiedad intelectual de
Xilinx, debido al alto grado de optimización que presentan, a
la flexibilidad de los mismos, y la integración con el entorno
de desarrollo del fabricante.
V. D ISE ÑO E IMPLEMENTACI ÓN DE LA UNIDAD DE
MEMORIA
Para la elección de la arquitectura propuesta en el apartado
V-B, se han analizado diferentes aspectos que hacen a la
organización de la memoria. Estos aspectos, se encuentran
detallados en el apartado V-A. Además, por su relación con
la unidad de memoria, en la sección V-C se presenta la
implementación del contador de programa.
Figura 6.
Representación gráfica de una unidad de memoria genérica.
1. Arquitectura Princeton o Von Neumann, donde las instrucciones de programa y los datos comparten la misma
unidad de memoria y buses.
2. Arquitectura Harvard, donde las instrucciones y los
datos son almacenados en memorias diferentes, y se
gestionan mediante buses independientes.
Debe notarse que, si se adopta la arquitectura Harvard, deben
elegirse los valores md , wd , mp y wp , donde el subı́ndice d
denota memoria de datos, y el subı́ndice p denota memoria de
programa.
Un último aspecto a tenerse en cuenta, consiste en la
implementación en hardware de los bloques de memoria. En
efecto, los dispositivos FPGA pueden implementar unidades
de memoria mediante bloques RAM dedicados, o utilizando esquemas distribuidos (basados en registros y tablas de
búsqueda). El primer esquema es útil para memorias grandes,
mientras el segundo permite reducir los retardos de propagación en memorias pequeñas.
B. Implementación de la unidad de memoria
En el presente trabajo se utiliza una arquitectura Harvard,
contando con una memoria de programa de wp = 512 palabras
de mp = 36 bits cada una. Asimismo, se tiene una memoria
de datos de wd = 512 palabras de md = 32 bits cada
una. Ambas memorias se implementan utilizando bloques de
memoria RAM dedicados, haciendo uso del Block Memory
Generator de Xilinx [41] e interconectándose mediante interfaz
nativa. Por un lado, la memoria de datos se modela como
una True Dual Port RAM con modo de operación Read-first
para ambos puertos, mientras que la memoria de programa
se modela como una Single Port ROM. Ambas memorias son
inicializadas mediante archivos COE.
La elección de esta arquitectura radica en la flexibilidad que
otorga tener palabras de instrucción mayores a las palabras de
datos, a la hora de diseñar el juego de instrucciones. Asimismo,
A. Consideraciones de la unidad de memoria
Las unidades de memoria se modelan generalmente como
un arreglo de w palabras, capaces de almacenar m bits cada
una. Esta descripción puede verse en forma esquemática en la
Figura 6.
Al momento de diseñar el sistema digital, es importante
elegir cuidadosamente los valores de w y m, de modo a
contar con suficiente memoria para almacenar las constantes,
resultados intermedios y variables de estado.
Otro aspecto importante en el diseño de la unidad de
memoria consiste en la elección de arquitectura, siendo las
alternativas:
Figura 7.
Esquema de una arquitectura de computadoras Princeton.
Figura 8.
Esquema de una arquitectura de computadoras Harvard.
RESUMEN EJECUTIVO
5
(a) SUM, MUL
una arquitectura Harvard permite un mayor throughput pues
los accesos a memoria se producen en forma independiente
para datos e instrucciones. La selección de bloques de memoria RAM dedicados, radica en el tamaño relativamente grande
de ambas memorias; no obstante, esto provee un margen para
aplicaciones más complejas.
(b) MOV
(c) JMP
C. Implementación del contador de programas
El contador de programa es el bloque funcional encargado
de controlar la memoria de programa, y de esta manera,
permitir la ejecución secuencial de instrucciones del código
de programa. En el presente trabajo, el contador de programa
fue implementado utilizando un contador ascendente sı́ncrono
de nueve bits, capaz de direccionar las 512 palabras de la
memoria de programa. Asimismo, cuenta con señales de incremento, y funcionalidad de sobrecarga. Esto último permite
implementar saltos incondicionales en el flujo de ejecución de
un programa.
VI. D ISE ÑO E IMPLEMENTACI ÓN DEL JUEGO DE
INSTRUCCIONES
El diseño del juego de instrucciones ha sido realizado
mediante un análisis previo del código de programa que resuelve el modelo matemático; las caracterı́sticas del mismo, ası́
como el algoritmo que implementa se detallan en el apartado
VI-A. Como resultado, en el apartado VI-B se presentan las
instrucciones implementadas en el diseño digital.
A. Código de programa y requerimientos mı́nimos
El sistema digital que implemente la técnica Hardware in
the Loop, debe resolver las ecuaciones (5), (9) y (10) en forma
iterativa. Para ello, el programa debe ser capaz de:
1. Almacenar los valores constantes,
2. Actualizar los valores de las entradas,
3. Calcular el valor de las variables de estado para el
siguiente instante,
4. Actualizar el valor de las salidas.
En efecto, estos pasos pueden esquematizarse de manera más
precisa y puntual, en el Algoritmo 1, que constituye el código
de programa que se utilizó en el diseño.
Algoritmo 1 Código de ejecución que resuelve el modelo
matemático.
Almacenar las constantes en memoria.
loop
Almacenar las entradas de tensión Va (k), Vb (k), Vc (k).
Calcular las entradas del sistema u1 (k), u2 (k), u5 (k).
Calcular el par eléctrico Te (k) haciendo uso de la ecuación (9).
Calcular las variables de estado en el instante k + 1,
haciendo uso de la ecuaciones (5) y (10).
Actualizar las variables de estado para la siguiente iteración x(k) ←− x(k + 1).
Esperar hasta cumplir la condición de muestreo.
end loop
Recordando el Análisis de operaciones realizado en la
página 3, para el procesamiento de los datos son necesarias
las instrucciones de suma (SUM) y multiplicación (MUL) de
(d) WATCH, FREEZE
Mnemónico
Código binario
Descripción a nivel de registros
SUM
MUL
JMP
WATCH
MOV
FREEZE
0001
0010
0100
0101
0110
0111
M[r3] ←− M[r1] + M[r2]
M[r3] ←− M[r1] * M[r2]
PC ←− r1
FIFO ←− resultado siguiente
M[r2] ←− INREG[r1]
INREG ←− INPUT
Figura 9. Juego de instrucción del sistema digital propuesto. En el formato
de instrucción, los campos que no son utilizados se señalan con color gris.
números reales. Por otro lado, verificando el pseudocódigo,
resulta evidente la necesidad de una instrucción para cargar
los valores en memoria. Para ello, podrı́a implementarse
una instrucción MOV que permita obtener los valores de
las entradas almacenados en registros. De igual manera, la
posibilidad de iterar a través de las instrucciones, implica el
uso de instrucciones de salto. Dado que la iteración se realiza
indefectiblemente, es posible utilizar un salto incondicional,
sin necesidad de implementar control de flujo. Ası́, podrı́a
utilizarse una instrucción JMP.
B. Implementación del juego de instrucciones
Además de las instrucciones planteadas en el apartado
anterior, en la unidad de control del presente trabajo se
han implementado dos instrucciones adicionales: WATCH que
permite almacenar temporalmente el resultado siguiente, para
su posterior envı́o por el módulo de comunicación; y FREEZE
que permite almacenar instantáneamente los valores de los
pines de entrada en unos registros. En la Figura 9 se observan
cada una de las instrucciones del juego de instrucción. Asimismo, se detalla los cuatro formatos de instrucción utilizados
y el número de bits correspondientes a cada campo. De igual
manera, se especifican los códigos binarios de operación para
cada instrucción, ası́ como la descripción de funcionamiento
en lenguaje de transferencia de registros (RTL).
VII. D ISE ÑO E IMPLEMENTACI ÓN DEL M ÓDULO DE RELOJ
Los aspectos que hacen a la temporización del sistema se
presentan a continuación. En particular, en el apartado VII-A
se analizan las condiciones de muestreo que debe cumplir el
sistema, en el apartado VII-B se introduce el modelo utilizado
para calcular el perı́odo que tarda en ejecutarse una instrucción, y en el apartado VII-C se presenta la implementación
del módulo de reloj para el sistema digital propuesto.
RESUMEN EJECUTIVO
6
0.08
0.07
0.06
Probabilidad
A. Restricciones de muestreo
Para el correcto funcionamiento de la técnica Hardware
in the Loop, el sistema digital debe ser capaz de actualizar
las señales de salida y las variables de estado, ante cualquier
variación en las entradas.
En efecto, durante un ciclo de cálculo, se ejecutan λ
instrucciones en perı́odos de Tins cada una. Al final de este
ciclo, se actualizan todas las señales de salida y variables de
estado. Si el perı́odo de muestreo de las señales de entrada es
Ts , para actualizar las señales de salida y variables de estado
antes de la siguiente muestra, debe cumplirse que:
0.05
0.04
0.03
0.02
0.01
0
Ts > λTins ,
(13)
que para una frecuencia de muestreo de 100 kHz, y suponiendo
que se ejecutan 100 instrucciones en cada ciclo de cálculo
resulta en:
Tins < 100 ns .
(14)
B. Perı́odo de instrucciones
En la ecuación (13) de la sección anterior, se ha considerado
que el tiempo Tins era homogéneo para cada instrucción.
Aunque esta suposición es útil para fines educativos, en
implementaciones reales es imposible de lograr. El motivo de
esta variación radica en los diferentes procesos involucrados en
ejecutar una instrucción. Dependiendo del tipo, una instrucción
puede constar de lectura de memoria, procesamiento de datos,
y/o escritura en memoria; donde el perı́odo de tiempo que
requiere cada uno de estos procesos varı́a en función a distintos
parámetros. En consecuencia el perı́odo Tins se modela como
Tins ≡ Tread + Twrite + Tprocessing + Tδ + Tguard ,
(15)
donde Tread , Twrite , Tprocessing representan respectivamente
los tiempos máximo de lectura, escritura en memoria y procesamiento de datos, y se estiman en forma estadı́stica a partir
de simulaciones. Asimismo, se considera el tiempo Tδ como
la suma de todos los retardos de propagación de datos; y se
agrega un tiempo Tguard de guarda para compensar cualquier
error estocástico y para dar mayor robustez al sistema.
C. Tmplementación del módulo de reloj
Con el fin de conocer los lı́mites del sistema propuesto,
en lo que respecta al valor de Tins , se realizaron pruebas de
software exhaustivas al modelo de la unidad de procesamiento
de la Figura 5.
Para ello, se han simulado más de 60.000 operaciones de
punto flotante y se ha medido el tiempo de ejecución de cada
una de ellas. El resultado de estas mediciones aparecen en
forma de histograma en la Figura 10, de la que se puede
concluir que Tprocessing es menor a 25 ns para todos los casos.
Mediante verificaciones similares, también se llegó a la
conclusión que Tread y Twrite son menores a 15 ns, y los
retardos de propagación Tδ se encuentran entre 2 y 10 ns.
A la vista de estos resultados, en este trabajo se ha optado
por un perı́odo de reloj principal Tclk de 20 ns, donde la lectura
y escritura en memoria se ejecutan en un perı́odo de reloj,
mientras que las instrucciones de procesamiento se ejecutan
en dos perı́odos. De esta manera, el perı́odo de instrucción es
Tins es de 80 ns, que cumple con las restricción impuesta en
la expresión (14).
5
10
15
20
Tiempo [ns]
25
30
Figura 10. Probabilidad de la ejecución de una operación de punto flotante,
en una determinada cantidad de tiempo.
Desde un punto de vista de más bajo nivel, el módulo
de reloj fue implementado haciendo uso del Clock Wizard
de Xilinx [42]. A partir de la señal generada por el reloj
diferencial de 200 MHz incorporado en la placa de evaluación,
el módulo de reloj produce la señal de reloj principal de
50 MHz (equivalente a un perı́odo de 20 ns). Asimismo, se
generan otras dos señales auxiliares de 125 MHz (8 ns) y
100 MHz (10 ns), que son utilizadas por el módulo de salida
y el módulo de entrada, respectivamente.
VIII. D ISE ÑO DEL M ÓDULO DE SALIDA
En las consideraciones de temporización se ha supuesto un
muestreo de 100 kHz. Si se considera además que el sistema
debe entregar las tres entradas y seis variables de salida de la
Figura 3, y cada una de ellas son números de punto flotante
de 32 bits; entonces, la tasa de bits asciende a:
Rraw = 100 × 103 × 9 × 32 bits = 28, 8 Mbps ,
(16)
para una transmisión de datos brutos. Esta velocidad se
elevarı́a aún más si el protocolo de transmisión contase con
campos de cabecera y cola.
Tradicionalmente, la comunicación entre un dispositivo
basado en FPGA y una computadora personal se realiza
mediante protocolos serial, paralelo, o I2 C, entre otros. Sin
embargo, ninguno de éstos es capaz de lograr en forma fiable,
tasas de transmisión tan elevadas como la necesaria para este
diseño. Por consiguiente, aparecen como alternativas viables
protocolos más complejos pero veloces como Fast Ethernet o
Gigabit Ethernet, SDI, SATA o PCI-express.
En el marco del presente trabajo, se optó por diseñar un
módulo de comunicación que implemente el protocolo Gigabit
Ethernet, haciendo uso de un bloque de propiedad intelectual
de Xilinx [43]. Esta elección de basa en el amplio uso del
protocolo Ethernet en telecomunicaciones, como también, su
presencia en casi todas las computadoras personales.
IX. D ISE ÑO DEL M ÓDULO DE ENTRADA
En las secciones anteriores han sido desarrollados varios
aspectos fundamentales para el cómputo de las ecuaciones (5),
(9) y (10), sin mencionarse en detalle cómo se adquieren las
tensiones trifásicas de entrada que aparecen en la Figura 3.
A la vista de esto, en el apartado IX-A se introducen las
caracterı́sticas generales de las señales de entradas, mientras
RESUMEN EJECUTIVO
Figura 11.
7
Figura 12.
Diagrama de bloques de la unidad de control.
Figura 13.
Diagrama de estados de la unidad de control.
Diagrama de bloques del módulo de entrada.
que en el apartado IX-B se presenta la implementación del
módulo de entrada propuesto.
A. Caracterización de la señal de entrada
Idealmente, las entradas del sistema representado en la
Figura 3 son tensiones sinusoidales puras. No obstante, en
la mayorı́a de las aplicaciones reales, las entradas están constituidas por tensiones moduladas en ancho de pulso (PWM).
Este tipo de señales presenta un inconveniente que consiste
en la existencia de tres valores estables Vmax , 0 y −Vmax ;
mientras que los sistemas digitales manejan únicamente dos
valores estables. Como consecuencia, es necesario diseñar un
mecanismo que permita representar la señal generada en el
dominio digital, para luego convertir el valor en un número de
punto flotante, capaz de operar en la unidad de procesamiento.
En el marco del presente trabajo se propone la representación
de señales PWM mediante una descomposición en signo y
magnitud, como:
VPWM = (−1)s × M × Vmáx
(17)
donde s representa el signo de la tensión, M representa el valor
en magnitud, y Vmáx es el valor pico de la tensión PWM.
B. Implementación del módulo de entrada
El funcionamiento del módulo de entrada implementado en
el marco del presente trabajo, puede verse esquematizado en la
Figura 11 donde las señales pwm representan las magnitudes
M de la señal PWM trifásica, mientras que la señales sign
representan los correspondientes signos s. Asimismo, el valor
pico Vmax es proporcionado al módulo mediante la señal
ivalue. La instrucción FREEZE almacena los valores de pwm
y sign en unos registros de entrada, activando la señal fetch;
esto permite que el muestreo sea determinı́stico para las tres
tensiones de entrada. Por otro lado, la señal addr permite
elegir la entrada PWM que aparece disponible a la salida dout
del módulo de comunicación; esto sucede cuando se recibe una
instrucción MOV.
X. D ISE ÑO E IMPLEMENTACI ÓN DE LA UNIDAD DE
CONTROL
La unidad de control tiene a su cargo comandar a los demás
bloques funcionales. Para ello, se encarga de la decodificación
de instrucciones obtenidas de la memoria de programa, como
también la generación de señales apropiadas para comandar
la unidad de procesamiento, memoria de datos, contador de
programa, módulo de entrada y módulo de salida. Entre las
funciones que realiza se encuentran:
1. Generar las señales para el incremento o sobrecarga del
contador de programa.
2. Generar las direcciones para lectura de memoria de
datos; y en el caso de escritura, generar las direcciones
y señales de escritura apropiadas.
3. Generar las señales de negación y selección de operación
en la unidad de procesamiento.
4. Proveer del valor pico de tensión al módulo de entrada
(en formato de punto flotante de precisión simple).
5. Generar las señales para almacenar y adquirir datos del
módulo de entrada.
6. Indicar al módulo de comunicación que un resultado
debe ser almacenado temporalmente para su envı́o.
La unidad de control implementada en el presente trabajo
puede ser observada en la Figura 12, mediante una representación en diagrama de bloques. El funcionamiento está divido
en dos bloques principales, el decoder que se encarga de
decodificar las instrucciones conforme aparecen en el bus ins;
y la máquina de estados finitas FSM que se encarga de generar
las señales de control en los instantes de tiempo apropiados.
Entre estos bloques se encuentra un conjunto de registros, que
permite almacenar temporalmente las señales decodificadas,
hasta que son utilizadas por la máquina de estados FSM.
Asimismo, se cuenta con un pequeño bloque WFSM que
implementa una máquina de estados secundaria, que sirve para
generar las señales de control cuando se tiene una instrucción
de tipo WATCH.
La máquina de estados FSM implementa un flujo de estados
como el que se observa en la Figura 13. Básicamente, se consta
de cuatro fases: las primeras tres corresponden a los estados
x1, x2 y x3, respectivamente. La cuarta fase, corresponde
indistintamente a los estados x4 y x5. Las instrucciones SUM,
MUL y MOV, que escriben valores en la memoria de datos,
hacen uso del estado x4. En contrapartida, las instrucciones
JMP, JMP y FREEZE, que no requieren escribir en la memoria
de datos, utilizan el estado x5.
XI. S ISTEMA DIGITAL COMPLETO
Como resultado de cada una de las consideraciones de
diseño expuestas anteriormente, el sistema digital completo
puede verse esquematizado en la Figura 14. En el diagrama de
bloques, se especifican las unidades funcionales del sistema, es
decir, la unidad de procesamiento, las memorias de programa
RESUMEN EJECUTIVO
8
Tabla I
PAR ÁMETROS F ÍSICOS DEL MOTOR AS ÍNCRONO TRIF ÁSICO EMPLEADO EN
LAS SIMULACIONES .
Sı́mbolo
Valor
Resistencia de estátor
Resistencia de rotor
Inductancia de dispersión de estátor
Inductancia de dispersión de rotor
Inductancia de magnetización de estátor
Coeficiente de inercia
Coeficiente de fricción viscosa
Par de polos
Frecuencia nominal
Rs (Ω)
Rr (Ω)
Lls (H)
Llr (H)
Lms (H)
Ji (kg m2 )
Bi (kg m2 /s)
P
fa (Hz)
10.0
6.3
0.43
0.43
0.4212
0.02
0.0022
1.0
50.0
Diagrama de estados de la unidad de control.
XII. S IMULACI ÓN Y PRUEBAS EXPERIMENTALES
Con el propósito de validar el diseño e implementación
del sistema Hardware in the Loop propuesto en las secciones
anteriores, fue diseñado el entorno de simulación genérico que
puede observarse en le Figura 15.
En el entorno de simulación genérico, el bloque Generación
trifásica se encarga de generar las tensiones de entrada Va , Vb
y Vc que excitan al motor. Asimismo, el bloque Modelo del
motor ası́ncrono trifásico implementa el modelo matemático
de la máquina de inducción, ejecutando el Algoritmo 1. Los
valores correspondientes a los parámetros fı́sicos y constructivos que fueron utilizados en las simulaciones se muestran en la
Tabla I, y como parámetros de simulación se han utilizado un
paso Tm = 10 µs, un tiempo inicial t = 0 s y tiempo de parada
t = 2 s. Por otro lado, el bloque Almacenamiento de datos,
almacena en formato de texto los valores de las entradas y
salidas de la Figura 3, y el tiempo de simulación t. Finalmente,
en el bloque Análisis de resultados fueron utilizados para
realizar los análisis preliminares el programa GNU/Octave y
para generar las gráficas finales gnuplot, y lualatex.
Con el propósito de comparar y contrastar los resultados
obtenidos, fueron diseñados dos entornos de simulación: uno
de ellos basado en hardware, utilizando el dispositivo FPGA;
y otro de ellos, basado en software ejecutándose en una
computadora personal. En el entorno por hardware el modelo
matemático del motor ası́ncrono trifásico fue implementado en
código binario correspondiente al diseño; mientras que en el
entorno por software el modelo del motor fue desarrollado
en un programa escrito en lenguaje C. A continuación se
presentan los resultados más representativos.
En la Figura 16 se observa la evolución temporal de las
salidas mecánicas par eléctrico y la velocidad angular del rotor,
mientras que en la Figura 17 se muestra la evolución temporal
de las corrientes iαs e iβs del estátor; todos a frecuencia
nominal fa = 50 Hz. Ambas figuras fueron elaboradas a partir
de los resultados obtenidos por hardware.
En las Figuras 18 y 19 se observa la evolución temporal
del par eléctrico Te y la velocidad angular del rotor ωr para
distintas frecuencias. A medida que la frecuencia fa de la
señal modulante fue disminuyendo, la respuesta se hizo más
rápida a costa de un incremento en el ruido y la aparición de
sobrepicos mayores.
Los resultados obtenidos en ambos entornos de simulación
resultaron idénticos en todas las simulaciones. Esto permite
concluir que el error es nulo entre los entornos de simulación.
De esta manera, resulta validado el diseño e implementación
del sistema digital propuesto, puesto que el mismo implementa exitosamente el modelo matemático del motor ası́ncrono
trifásico en operaciones de punto flotante de precisión simple.
14
12
10
8
(a)
Par Te [Nm]
y datos, el contador de programas, los módulos de entrada y
salida, la unidad de control y el módulo de reloj. Asimismo, se
indica mediante lı́neas llenas, el flujo de datos entre bloques
funcionales, y mediante lı́neas punteadas, la relación entre los
bloques y el módulo de reloj.
6
4
2
0
-2
-4
0
0.2
0.4
0.6
0.8
Tiempo [s]
1
1.2
1.4
1.6
0
0.2
0.4
0.6
0.8
Tiempo [s]
1
1.2
1.4
1.6
350
300
(b)
Velocidad angular ωr [rad/s]
Figura 14.
Parámetro
250
200
150
100
50
0
Figura 15.
Diagrama de bloques de un entorno de simulación genérico.
Figura 16. Evolución temporal a frecuencia nominal del (a) Par eléctrico,
(b) Velocidad angular.
RESUMEN EJECUTIVO
9
300
20
200
180
Corriente iαs [A]
10
(a)
(a)
5
200
150
(b)
100
Velocidad angular ωr [rad/s]
15
Velocidad angular ωr [rad/s]
250
50
0
160
140
120
100
80
60
40
20
0
-5
0
0.2
0.4
0.6
0.8
0
1
0
0.2
0.4
Tiempo [s]
0.6
0.8
1
0.6
0.8
1
Tiempo [s]
140
70
120
60
-20
0
0.2
0.4
0.6
0.8
Tiempo [s]
1
1.2
1.4
(c)
1.6
20
100
80
(d)
60
40
Velocidad angular ωr [rad/s]
-15
Velocidad angular ωr [rad/s]
-10
20
15
0
50
40
30
20
10
0
0.2
0.4
0.6
0.8
0
1
0
0.2
0.4
Tiempo [s]
30
5
0
(e)
-5
-10
0
0.2
0.4
0.6
0.8
Tiempo [s]
1
1.2
1.4
1.6
10
0
0.2
0.4
0.6
0.8
1
Figura 19.
Evolución temporal de la velocidad angular del rotor ωr a
frecuencias menores que la nominal, en simulaciones por hardware. (a)
Frecuencia fa = 40 Hz. (b) Frecuencia fa = 30 Hz. (c) Frecuencia
fa = 20 Hz. (d) Frecuencia fa = 10 Hz. (e) Frecuencia fa = 5 Hz.
35
30
15
10
(b)
5
Par Te [Nm]
25
Par Te [Nm]
15
Tiempo [s]
20
20
15
10
5
0
0
-5
20
0
Figura 17. Evolución temporal a frecuencia nominal de la (a) Corriente ias
del estátor, (b) Corrientes ibs estátor.
(a)
25
5
-15
-20
Velocidad angular ωr [rad/s]
Corriente iβs [A]
10
(b)
Tiempo [s]
35
0
0.2
0.4
0.6
0.8
-5
1
0
0.2
0.4
Tiempo [s]
0.6
0.8
1
Tiempo [s]
60
50
50
40
de máquinas eléctricas y sistemas fı́sicos. Por estos motivos,
es posible concluir que el diseño propuesto constituye una
opción útil para simulaciones Hardware in the Loop, y en
particular, para la validación del diseño de controladores de
motores ası́ncronos trifásicos.
En lo que respecta a las futuras lı́neas de investigación a
partir del desarrollo de este trabajo, podrı́an ser:
40
(d)
20
Par Te [Nm]
(c)
Par Te [Nm]
30
30
20
10
10
0
0
-10
0
0.2
0.4
0.6
0.8
-10
1
0
0.2
0.4
Tiempo [s]
0.6
0.8
1
Tiempo [s]
30
25
(e)
Par Te [Nm]
20
15
10
5
0
-5
-10
0
0.2
0.4
0.6
0.8
1
Tiempo [s]
Figura 18. Evolución temporal del par eléctrico Te a frecuencias menores
que la nominal, en simulaciones por hardware. (a) Frecuencia fa = 40 Hz.
(b) Frecuencia fa = 30 Hz. (c) Frecuencia fa = 20 Hz. (d) Frecuencia
fa = 10 Hz. (e) Frecuencia fa = 5 Hz.
XIII. C ONCLUSI ÓN Y TRABAJOS FUTUROS
En el marco de este Trabajo Final de Grado, se ha diseñado
un sistema digital basado en FPGA de la técnica Hardware
in the Loop, aplicado a un motor ası́ncrono trifásico. Para
ello, ha sido desarrollado el modelo matemático de la máquina
ası́ncrona trifásica, y en función al modelo, se han diseñado
los distintos bloques funcionales que componen al sistema,
ası́ como el código de programa; para finalmente llevar a la
implementación del diseño en una placa de evaluación. Las
consideraciones hechas a lo largo del diseño resultaron en un
diseño robusto y flexible, que presentó un error nulo en las
pruebas experimentales. En este sentido, cabe destacar además,
que la flexibilidad del sistema permite plantear otros tipos
1. La introducción de nuevas caracterı́sticas al diseño digital propuesto, tales como: implementar una comunicación bidireccional con auto-negociación Ethernet
10/100/1000; extender la arquitectura y caracterı́sticas
de la unidad de procesamiento para incluir operaciones
lógicas sobre datos de 32 bits, saltos incondicionales,
pruebas lógicas del tipo if-else, y periféricos tales como
contadores y temporizadores; implementar un sistema
de interrupciones, capaz de modificar el flujo normal
del código de programa.
2. La optimización del diseño digital propuesto, incluyendo: reducir la frecuencia de reloj, utilizar una unidad
de procesamiento basada en operaciones de punto fijo,
e implementar un esquema de paralelización para las
operaciones de suma y multiplicación.
3. Modelar otros sistemas fı́sicos, relacionados o no con
sistemas de potencia.
4. Desarrollar investigaciones en el campo de las telecomunicaciones, utilizando el protocolo Ethernet y haciendo
uso de los diferentes periféricos con que cuenta el
módulo de evaluación.
R EFERENCIAS
[1] R. Isermann, J. Schaffnit, and S. Sinsel, “Hardware-in-the-loop simulation for the design and testing of engine-control systems,” Control
Engineering Practice, vol. 7, no. 5, pp. 643–653, 1999.
[2] Q. Wu, L. Lei, J. Chen, and W. Wang, “Research on hardware-in-theloop simulation for advanced front-lighting system,” in Computational
Intelligence and Industrial Application, 2008. PACIIA’08. Pacific-Asia
Workshop on, vol. 2. IEEE, 2008, pp. 671–675.
RESUMEN EJECUTIVO
[3] M. Short and M. Pont, “Hardware in the loop simulation of embedded
automotive control system,” in Proceedings of the 8th International
IEEE Conference on Intelligent Transportation Systems. IEEE, 2005,
pp. 426–431.
[4] J. Brunet and L. Flambard, “A hardware in the loop (hil) model
development and implementation methodology and support tools for
testing and validating car engine electronic control unit (ecu),” The
International Conferences on CAE and Computational Technologies for
Industry.(TCN CAE), pp. 5–8, 2005.
[5] S. Raman, N. Sivashankar, W. Milam, W. Stuart, and S. Nabi, “Design
and implementation of hil simulators for powertrain control system software development,” in American Control Conference, 1999. Proceedings
of the 1999, vol. 1. IEEE, 1999, pp. 709–713.
[6] B. Powell, N. Sureshbabu, K. Bailey, and M. Dunn, “Hardware-inthe-loop vehicle and powertrain analysis and control design issues,” in
American Control Conference, 1998. Proceedings of the 1998, vol. 1.
IEEE, 1998, pp. 483–492.
[7] C. Frangos, “Control system analysis of a hardware-in-the-loop simulation,” Aerospace and Electronic Systems, IEEE Transactions on, vol. 26,
no. 4, pp. 666–669, 1990.
[8] T. Sudiyanto, A. Budiyono, and H. Sutarto, “Hardware in-the-loop
simulation for control system designs of model helicopter,” eMR, vol. 16,
no. 1, p. 8, 2005.
[9] B. Naasz, R. Burns, D. Gaylor, and J. Higinbotham, “Hardware in the
loop testing of continuous control algorithms for a precision formation
flying demonstration mission,” in 18th International Symposium on
Space Flight Dynamics, vol. 548, 2004, p. 53.
[10] N. Gans, W. Dixon, R. Lind, and A. Kurdila, “A hardware in the loop
simulation platform for vision-based control of unmanned air vehicles,”
Mechatronics, vol. 19, no. 7, pp. 1043–1056, 2009.
[11] J. Toman, Z. Ančı́k, and V. Singule, “Hardware-in-the-loop testing of
control algorithms for brushless dc motor,” in Mechatronics. Springer,
2012, pp. 165–173.
[12] A. Saleem, R. Issa, and T. Tutunji, “Hardware-in-the-loop for on-line
identification and control of three-phase squirrel cage induction motors,”
Simulation Modelling Practice and Theory, vol. 18, no. 3, pp. 277–290,
2010.
[13] C. Graf, J. Maas, T. Schulte, and J. Weise-Emden, “Real-time hilsimulation of power electronics,” in Industrial Electronics, 2008. IECON
2008. 34th Annual Conference of IEEE. IEEE, 2008, pp. 2829–2834.
[14] B. Lu, X. Wu, H. Figueroa, and A. Monti, “A low-cost real-time
hardware-in-the-loop testing approach of power electronics controls,”
Industrial Electronics, IEEE Transactions on, vol. 54, no. 2, pp. 919–
931, 2007.
[15] O. Crăciun, A. Florescu, I. Munteanu, A. I. Bratcu, S. Bacha, and
D. Radu, “Hardware-in-the-loop simulation applied to protection devices
testing,” International Journal of Electrical Power & Energy Systems,
vol. 54, pp. 55–64, 2014.
[16] M. Kähler, R. Souffrant, S. Dryba, D. Kluess, R. Bader, and C. Woernle,
“Hardware-in-the-loop-simulator for testing of total hip endoprostheses,”
in 4th European Conference of the International Federation for Medical
and Biological Engineering. Springer, 2009, pp. 1785–1788.
[17] R. Souffrant, M. Kähler, S. Dryba, D. Kluess, R. Bader, and C. Woernle,
“Hardware-in-the-loop-simulator for testing of knee endoprostheses,”
in World Congress on Medical Physics and Biomedical Engineering,
September 7-12, 2009, Munich, Germany. Springer, 2010, pp. 2120–
2123.
[18] S. Herrmann, R. Rachholz, R. Souffrant, M. Kaehler, J. Zierath,
D. Kluess, C. Woernle, and R. Bader, “Development of a threedimensional musculoskeletal model for the hardware-in-the-loop joint
simulation,” in 6th World Congress of Biomechanics (WCB 2010).
August 1-6, 2010 Singapore. Springer, 2010, pp. 557–560.
[19] B. Hanson, M. Levesley, K. Watterson, and P. Walker, “Hardware-in-theloop-simulation of the cardiovascular system, with assist device testing
application,” Medical engineering & physics, vol. 29, no. 3, pp. 367–
374, 2007.
[20] Y. Chapuis, L. Zhou, D. Casner, H. Ai, and Y. Hervé, “Fpga-in-the-loop
for control emulation of distributed mems simulation using vhdl-ams,”
in Hardware and Software Implementation and Control of Distributed
MEMS (DMEMS), 2010 First Workshop on. IEEE, 2010, pp. 92–99.
[21] Z. Jiang, R. Leonard, R. Dougal, H. Figueroa, and A. Monti, “Processorin-the-loop simulation, real-time hardware-in-the-loop testing, and hardware validation of a digitally-controlled, fuel-cell powered batterycharging station,” in Power Electronics Specialists Conference, 2004.
PESC 04. 2004 IEEE 35th Annual, vol. 3. IEEE, 2004, pp. 2251–
2257.
[22] H. Temeltas, M. Gokasan, S. Bogosyan, and A. Kilic, “Hardware in the
loop simulation of robot manipulators through internet in mechatronics
education,” in IECON 02 [Industrial Electronics Society, IEEE 2002
28th Annual Conference of the], vol. 4. IEEE, 2002, pp. 2617–2622.
10
[23] R. Wells, J. Fisher, Y. Zhou, B. Johnson, and M. Kyte, “Hardware and
software considerations for implementing hardware-in-the loop traffic
simulation,” in Industrial Electronics Society, 2001. IECON’01. The 27th
Annual Conference of the IEEE, vol. 3. IEEE, 2001, pp. 1915–1919.
[24] D. Bullock, B. Johnson, R. B. Wells, M. Kyte, and Z. Li, “Hardwarein-the-loop simulation,” vol. 12, no. 1. Elsevier, 2004, pp. 73–89.
[25] R. Duelks, F. Salewski, and S. Kowalewski, “A real-time test and
simulation environment based on standard fpga hardware,” in Testing:
Academic and Industrial Conference-Practice and Research Techniques,
2009. TAIC PART 09. IEEE, 2009, pp. 197–204.
[26] D. Majstorovic, I. Celanovic, N. Teslic, N. Celanovic, and V. Katic,
“Ultralow-latency hardware-in-the-loop platform for rapid validation of
power electronics designs,” Industrial Electronics, IEEE Transactions
on, vol. 58, no. 10, pp. 4708–4716, 2011.
[27] F. Adler, A. Benigni, H. Stagge, A. Monti, and R. De Doncker, “A
new versatile hardware platform for digital real-time simulation: Verification and evaluation,” in Control and Modeling for Power Electronics
(COMPEL), 2012 IEEE 13th Workshop on. IEEE, 2012, pp. 1–8.
[28] P. Krause, O. Wasynczuk, S. Sudhoff, and IEEE Power Engineering
Society, Analysis of electric machinery and drive systems, 2nd ed., ser.
IEEE Press series on power engineering. IEEE Press, 2002.
[29] R. Reginatto, “Modelagem do motor de induçao,” Universidade Federal
do Rio Grande de Sul, Porto Alegre, Brasil, Relatório Técnico, Feb.
2006.
[30] R. Gregor, J. Balsevich, and B. Bogado, “Reduced-order observer for
rotor current estimation in speed control of dual-three phase induction
machine,” in Power Engineering, Energy and Electrical Drives (POWERENG), 2011 International Conference on. IEEE, 2011, pp. 1–6.
[31] N. Ab Aziz, “Three-phase squirrel-cage induction motor drive analysis
using labview,” Master’s thesis, University of South Australia, Adelaide,
Australia, Jul. 2006.
[32] J. Aller, Máquinas Eléctricas Rotativas: Introducción a la Teorı́a General, 1st ed., C. Pacheco, Ed. Caracas, Venezuela: Editorial Equinoccio:
Universidad Simón Bolı́var, 2007.
[33] P. C. Krause and C. H. Thomas, “Simulation of symmetrical induction
machinery,” Power Apparatus and Systems, IEEE Transactions on,
vol. 84, no. 11, pp. 1038 –1053, Nov. 1965.
[34] Xilinx, Inc., Spartan-6 Family Overview, 2nd ed., Xilinx, Inc., Oct. 2011,
DS160.
[35] ——, SP605 Hardware User Guide, 1st ed., Xilinx, Inc., Feb. 2011,
UG526.
[36] ——, Getting Started with the Xilinx Spartan-6 FPGA SP605 Evaluation
Kit, 1st ed., Xilinx, Inc., Mar. 2011, uG525.
[37] ——, FMC XM105 Debug Card User Guide, 1st ed., Xilinx, Inc., Jun.
2011, uG537.
[38] ——, ISE In-Depth Tutorial, 14th ed., Xilinx, Inc., Apr. 2012, uG695.
[39] ——, ISE Simulator (ISim) In-Depth Tutorial, 14th ed., Xilinx, Inc.,
Oct. 2012, uG682.
[40] ——, LogiCORE IP Floating-Point Operator v5.0, 5th ed., Xilinx, Inc.,
Mar. 2011, dS335.
[41] ——, LogiCORE IP Block Memory Generator v7.1, 7th ed., Xilinx, Inc.,
Apr. 2012, dS512.
[42] ——, LogiCORE IP Clocking Wizard v5.0, Xilinx, Inc., Mar. 2013.
[43] ——, LogiCORE IP Tri-Mode Ethernet MAC v5.5, 1st ed., Xilinx, Inc.,
Dec. 2012.