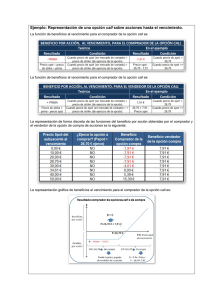
ejemplo de los capitulos
Anuncio

2 FUTUROS DE RENTA VARIABLE EL PRECIO TEÓRICO DEL FUTURO Un futuro es un contrato a plazo negociado en un mercado organizado en el que a fecha de hoy se fija el precio de compraventa de un activo que se intercambiará en un momento posterior. A continuación explicaremos el proceso por el que se determina el precio al que se va a realizar la transacción económica a plazo. El nombre del contrato, futuro, puede dar lugar a equívocos al asociarse a incertidumbre. Sin embargo, nada más alejado de la realidad. Futuro implica seguridad: fijar hoy el precio de una transacción económica a plazo independientemente de cuál sea la evolución del precio del activo objeto de intercambio. El siguiente cuadro recoge cotizaciones de los contratos de futuro negociados en MEFF el 2 de marzo de 2006: CUADRO 1 37 OPCIONES Y FUTUROS DE RENTA VARIABLE: MANUAL PRÁCTICO: En la columna de "contado" aparece el precio de las acciones en ese momento, mientras que bajo el epígrafe "futuros" cotizan las transacciones económicas a plazo de dichas acciones con vencimiento 17 de marzo de 2006. Como podemos observar, existen diferencias entre el precio de futuro y el precio de contado. Algunos activos (como Repsol YPF) tienen su precio de futuro por encima del contado y otros (como Gas Natural) lo tienen por debajo. ¿Tiene esto algo que ver con expectativas alcistas o bajistas sobre la evolución del precio de las acciones? Tal y como vamos a ver a continuación, la respuesta es no. El precio del futuro es aquél que hace financieramente equivalente comprar el activo hoy o hacerlo en la fecha de vencimiento. Por lo tanto, responde a la siguiente fórmula en la que existen dos partes bien diferenciadas: la capitalización del activo y el pago de dividendos. ti x d ti’ x d’ Precio Futuro = Precio Contado (1 + ) - Dividendos (1 + ) 360 360 ti = tipo de interés libre de riesgo desde la fecha de cálculo hasta el vencimiento. ti’ = tipo de interés libre de riesgo desde que se recibe el dividendos hasta la fecha de vencimiento. Es un tipo forward. d = días hasta el vencimiento. d’ = Días desde que se paga el dividendo hasta el vencimiento. La capitalización incrementa el precio del futuro sobre el precio de contado para recoger el coste de oportunidad que supone retrasar la compra del activo hasta la fecha de vencimiento. Por otro lado, el dividendo disminuye el precio del futuro con respecto al precio de contado ya que, al comprar el activo en la fecha de vencimiento, el inversor no va a ingresar los dividendos desembolsados con anterioridad. Además, esta cantidad también se invierte al tipo de interés libre de riesgo durante el tiempo que queda hasta el vencimiento. Es importante destacar que, en el caso de los dividendos, se utiliza el tipo de interés forward que media desde que se reparten hasta la fecha de vencimiento. Otra alternativa que evita el cálculo del tipo de interés forward, sería actualizar los dividendos al tipo de contado y después capitalizarlo todo hasta la fecha de vencimiento: [ Precio Futuro = Precio Contado - Dividendo (1 + ti’ x d’ 360 ] ) (1 + ti x d ) 360 ti = tipo de interés libre de riesgo desde la fecha de cálculo hasta el vencimiento. ti’ = tipo de interés libre de riesgo desde la fecha de cáculo hasta la fecha de pago del dividendo. d = días hasta el vencimiento. d’ = Días hasta el pago del dividendo. Según lo anterior, el precio del futuro no responde a ningún tipo de expectativas (éstas las incorpora el precio de contado) sino que tan solo tiene en cuenta los tipos de interés, dividendos y tiempo al vencimiento, pudiendo cotizar: z Con prima o contango: el precio del futuro cotiza por encima del precio de contado. La capitalización del activo es superior al descuento de dividendos o no hay pago de los mismos. z Con descuento o Backwardation: el precio del futuro cotiza por debajo del precio de contado. Hay pago de dividendos y éstos son una cantidad superior a la capitalización del activo. 38 FUTUROS DE RENTA VARIABLE 2 Veamos un ejemplo numérico a partir de las cotizaciones de Endesa del 2 de marzo de 2006: CUADRO 2 COTIZACIÓN DE LA ACCIÓN Y FUTUROS DE ENDESA Como se ha comentado, la diferencia entre el último precio cruzado de contado (27,48€) y el último precio cruzado del futuro con vencimiento el 16 de junio de 2006 (27,67€), no responde a expectativas de revalorización de Endesa para ese periodo, sino que simplemente establece la equivalencia entre comprar el 2 de marzo a 27,48€ o comprar el 16 de junio a 27,67€. Se trata de una misma cantidad pero en diferentes momentos del tiempo. Puesto que hay 106 días entre las dos fechas consideradas, la inversión de 27,48€ al tipo de interés libre de riesgo (EuriborI) durante ese periodo generaría exactamente 27,67€. Puesto que Endesa no paga ningún dividendo entre el 2 de marzo y el 16 de junio, la relación contado/futuro recoge exclusivamente el tipo de interés libre riesgo. 27,67 = 27,48 (1 + 2,35% x 106 ) 360 En el siguiente gráfico se representa la evolución del Índice IBEX 35® y del Futuro sobre IBEX 35® correspondiente a la sesión del 2 de marzo de 2006. GRÁFICO 1 INDICE IBEX 35® VS FUTURO IBEX 35® 11.550 11.540 11.530 11.520 11.510 11.500 11.490 11.480 11.470 11.460 11.450 11.440 17.00 16.00 15.00 14.00 13.00 12.00 11.00 10.00 9.00 Futuro Contado 39 OPCIONES Y FUTUROS DE RENTA VARIABLE: MANUAL PRÁCTICO: Se observa que cualquier cambio en el precio de las acciones se refleja inmediatamente en la cotización del futuro, por lo que la diferencia entre contado y futuro, que denominamos "base", se mantiene más o menos constante a lo largo de la sesión. Según la fórmula descrita anteriormente, esta base es el reflejo de la relación existente entre el tipo de interés libre de riesgo y de los dividendos que pague el activo hasta el vencimiento. Lógicamente, en la fecha en que expira el contrato la base debe ser cero. Si por cualquier motivo esta relación de equilibrio se rompe, inmediatamente actuarán los denominados arbitrajistas corrigiendo la ineficiencia en el proceso de formación de precios. Pongamos un ejemplo: Supongamos que el precio del futuro de Endesa no fuera 27,67€ sino 28€. El tipo de interés que estaría relacionando contado y futuro sería 6,43% (recordemos que el Euribor para el plazo considerado es 2,35%). Se genera por lo tanto una ineficiencia en la formación del precio del futuro que el mercado inmediatamente corregiría mediante la intervención de los arbitrajistas. Éstos tratan de obtener beneficios aprovechando dichas ineficiencias y logrando simultáneamente eliminarlas mediante la corrección de los precios. En nuestro ejemplo, un arbitrajista realizaría la siguiente operación: z Pedir un préstamo al tipo Euribor (2,35%) de 2.748€ (+2.748€) z Comprar 100 acciones de Endesa a 27,48€ (-2.748€) z Vender 1 futuro de Endesa a 28€ (cada futuro tiene un nominal de 100 acciones). En la fecha de vencimiento: z Cumple con la obligación de venta de 100 acciones a 28€ (+2.800€) z Devuelve el préstamo solicitado de 2.767€ (-2.748€ de principal y -19€ de intereses). Rendimiento total: 2.800€ - 2.767€ = +33€ Cabe destacar los siguientes aspectos con respecto a esta operativa del arbitrajista: 1. Compra a un precio y vende a otro superior en el mismo momento del tiempo, sin riesgo ni incertidumbre. 2. Compra contado (infravalorado) lo cual presiona el precio al alza y vende futuro (sobrevalorado) lo cual presiona el precio a la baja. Por lo tanto, los precios tenderán a equilibrarse de nuevo. En resumen, el precio del futuro de un activo guarda una relación directa con el precio del activo en cuestión, los tipos de interés, los dividendos y el tiempo hasta el vencimiento. Cualquier otro precio que no satisfaga esa relación, será arbitrable y por tanto corregido de inmediato por el mercado. Vamos a complicar un poco la operación de arbitraje anterior poniendo un ejemplo de cómo una entidad puede cotizar la horquilla de precios del futuro de un activo. Los datos de partida son los siguientes: Quedan 98 días a vencimiento (hoy es 11 de diciembre de 2009 y el vencimiento es el 19 de marzo de 2010). 40 FUTUROS DE RENTA VARIABLE 2 La cotización de la acción de BBVA es: CUADRO 3 COTIZACIÓN DE LA ACCIÓN DE BBVA El tipo de interés libre de riesgo a 98 días es 0,74%. Podemos conseguir prestadas acciones de BBVA a cambio de un 2%. No hay pago de dividendos. Precio de venta (ask): para que alguien pueda asegurarse el precio de compra de unas acciones en una fecha futura, la entidad tendrá que contraer la obligación de venderlas. Para ello, deberá realizar las siguientes operaciones: -HOY: z Pedir prestado dinero al tipo de interés libre de riesgo (+1.218€) z Con el dinero del préstamo comprar las acciones (-1.218€) z Si hubiera dividendos los ingresaría, por lo que habría que restarlos al precio futuro. -VENCIMIENTO: z Tiene la obligación de vender las acciones al precio futuro pactado (X) z Devuelve el préstamo y los intereses (-1.220,44€) ¿Cuál debería ser el precio de venta del futuro? Claramente el que permite recuperar los 1.220,44€ que ha costado mantener las acciones hasta el vencimiento, por lo tanto la cotización será 12,21€. Precio de compra (bid): para que alguien pueda asegurarse el precio de venta de unas acciones en una fecha futura, la entidad tendrá que contraer la obligación de comprarlas. Para ello deberá realizar las siguientes operaciones: -HOY: z Pedir prestadas temporalmente las acciones a cambio de "un alquiler" (2%) z Vender las acciones en el mercado (+1.217€) z El dinero obtenido de la venta de acciones se invierte al tipo de interés libre de riesgo. (-1.217€) 41 3 LA PRIMA DE LAS OPCIONES LAS OPCIONES FINANCIERAS: EL VALOR INTRÍNSECO Y EL VALOR TEMPORAL Los contratos de opción son derechos que otorgan a su poseedor la posibilidad comprar (en el caso de un call) o vender (en el caso de un put) un activo subyacente a un precio determinado (precio de ejercicio) en una fecha de vencimiento a cambio del pago de una cantidad llamada prima. Aunque pueda parecer que se trata de activos desarrollados recientemente, las opciones se han venido negociando desde hace siglos. Por ejemplo, existen referencias del enriquecimiento de Tales de Mileto con unas opciones sobre aceitunas, al realizar una previsión adecuada de cuál sería la evolución de una determinada cosecha. Otro ejemplo más próximo en el tiempo sería el activo mercado de opciones (llamadas Opsies) creado en Ámsterdam en el siglo XVIII. Sin embargo, la industria de las opciones da un gran salto cuantitativo en 1973 cuando Fischer Black y Myron Scholes publican su artículo “The Pricing of Options and Corporate Liabilities” en el que encuentran la solución para valorar opciones financieras (trabajos desarrollados 10 años antes no lo lograron o quedaron incompletos: (Samuelson, Sprenkle, etc.) Por otro lado y de manera simultánea, Robert Merton publicó "Theory of Rational Option Pricing". Todos ellos son los padres de la teoría de valoración de opciones, razón por la cual Scholes y Merton recibieron el premio Nóbel en 1997 (Black murió en 1995, de no ser así seguramente también lo habría obtenido). La famosa fórmula de Black-Scholes y el resto de sus variaciones (Merton, Black 76, etc.) se utiliza actualmente para calcular el precio de las opciones. Y es precisamente la prima de las opciones lo que vamos a explicar, intentando aproximarnos de momento a ella de manera intuitiva, evitando la formulación matemática asociada. 87 OPCIONES Y FUTUROS DE RENTA VARIABLE: MANUAL PRÁCTICO: Para empezar, la primera pregunta que vamos a tratar de responder es la siguiente: ¿Cuánto estaría dispuesto a pagar por tener derecho a comprar (opción call) dentro de 6 meses acciones de Repsol a 21€ cuando ahora mismo está cotizando a 22€? ¿1,10€? ¿0,25€? ¿2,05€? Difícil ¿verdad? Para poder contestar a esta pregunta hay que tener en cuenta los siguientes factores: z Precio del activo subyacente: precio del activo objeto de intercambio que puede estar constantemente variando. z Precio de ejercicio: precio pactado para comprar o vender según sea call o put respectivamente. z Tiempo a vencimiento: tiempo que queda hasta el día en que expira el contrato. z Volatilidad futura: fluctuación estimada del activo subyacente hasta la fecha de vencimiento. z Tipo de interés libre de riesgo hasta el día de vencimiento. z Dividendos: rendimientos que genera el activo subyacente entre el momento de compra o venta y la fecha de vencimiento. Teniendo en cuenta los parámetros anteriores, a la hora de fijar la prima de una opción de compra sobre Repsol con precio de ejercicio 21€ y vencimiento dentro de 6 meses, podemos intuir los siguientes aspectos: z El precio del activo subyacente va a ser un factor clave: si Repsol cotiza a 20€ deberá subir por encima de 21€ para que el call proporcione algún beneficio en la fecha de vencimiento, mientras que si Repsol cotiza a 22€ el tenedor de la opción podría estar interesado en ejercerla en este mismo momento. z Otro aspecto muy importante es el tiempo que queda hasta la fecha de vencimiento. Si estamos hablando de un período de seis meses, puede ocurrir casi cualquier cosa con el precio del activo subyacente, mientras que si solo queda un día, salvo que ocurra un acontecimiento muy especial, el activo subyacente estará a un precio parecido al de hoy, por encima o por debajo, pero no muy alejado. Lo comentado anteriormente se puede resumir en una composición de la prima como suma de dos factores: valor intrínseco y valor temporal o extrínseco. PRIMA = VALOR INTRÍNSECO + VALOR TEMPORAL El valor intrínseco es el beneficio que proporcionaría una opción si se ejerciese en el mismo momento en que se está valorando. Por lo tanto, este componente va a ser siempre igual o mayor que cero (ver gráficos 1 y 2). Aunque nos estemos adelantando un poco, es necesario comentar que casi nunca suele ser óptimo este ejercicio anticipado de opcionesII, salvo en casos muy concretos(3), precisamente porque solo se ganaría el valor intrínseco, mientras que si vendiera la opción en mercado se obtendría el valor intrínseco más el valor temporal. 88 LA PRIMA DE LAS OPCIONES 3 GRÁFICO 1 VALOR INTRÍNSECO CALL@100 30 25 20 15 10 5 75 77 79 81 83 85 87 89 91 93 95 97 99 101 103 105 107 109 111 113 115 117 119 121 123 125 0 GRÁFICO 2 VALOR INRÍNSECO PUT@100 30 25 20 15 10 5 75 77 79 81 83 85 87 89 91 93 95 97 99 101 103 105 107 109 111 113 115 117 119 121 123 125 0 Por ejemplo, si el activo subyacente (PS) cotiza a 21€, el valor intrínseco (VI) de las siguientes opciones se calculará a partir de su correspondiente precio de ejercicio (PE) aplicando la fórmula: CUADRO 1 VI Call = Max(PS – PE,0) Call PE 20, VI = 1€ VI Put = Max(PE – PS,0) Put PE 20, VI = 0€ Call PE 22, VI = 0€ Put PE 22, VI = 1€ 89 OPCIONES Y FUTUROS DE RENTA VARIABLE: MANUAL PRÁCTICO: Evitando cálculos matemáticos complejos, de momento, definiremos el valor temporal de una opción como el importe en que la totalidad de la prima excede al valor intrínseco. Se trata de la cantidad adicional que el inversor está dispuesto a pagar por beneficiarse de una evolución favorable de los precios limitando su pérdida a la prima desembolsada ante una evolución desfavorable. Por lo tanto, a partir del tiempo a vencimiento y habida cuenta de la volatilidad esperada del activo subyacente, se estima en qué niveles (máximo y mínimo) podría estar el activo subyacente en la fecha en la que expira la opción. Es decir, estaremos dispuestos a desembolsar prima en función de la probabilidad que haya de ganar dinero con esa opción, por lo que cuanta más incertidumbre haya más valor temporal estaremos dispuestos a pagar (ver gráfico 3). GRÁFICO 3 VALOR TEMPORAL CALL Y PUT@100 8 7 6 5 4 3 2 1 75 77 79 81 83 85 87 89 91 93 95 97 99 101 103 105 107 109 111 113 115 117 119 121 123 125 0 El valor temporal es máximo para aquellas opciones cuyo precio de ejercicio se encuentra próximo al nivel del activo subyacente, ya que son las que incorporan una mayor incertidumbre sobre su probabilidad de ejercicio. Aquellas opciones cuyo precio de ejercicio se encuentra más alejado del activo subyacente suponen una menor incertidumbre y, por lo tanto, su valor temporal es más pequeño. Por consiguiente, el valor intrínseco se calcula directamente a partir del precio del activo subyacente y el precio de ejercicio. Sin embargo, en el cálculo del valor temporal influirán otros factores comentados anteriormente, especialmente el tiempo a vencimiento y la volatilidad. Estos dos componentes son básicos para la valoración de opciones y están muy relacionados entre sí: para que la volatilidad se pueda traducir en variabilidad de precios tiene que haber tiempo a vencimiento y viceversa. Por esta razón el valor temporal de las opciones se va erosionando hasta que en la fecha de vencimiento es cero (ver gráfico 4). Cabe destacar cómo el valor temporal decae más rápidamente cuanto menos tiempo queda el vencimiento, debido a que existe una mayor una certeza sobre la probabilidad de ejercicio de la opción. A mayor incertidumbre sobre el ejercicio, mayor valor temporal y viceversa. 90 LA PRIMA DE LAS OPCIONES 3 GRÁFICO 4 EVOLUCIÓN DEL VALOR TEMPORAL A VENCIMIENTO PRIMA Valor Temporal Valor Temporal Valor Intrínseco TIEMPO A vto VENCIMIENTO En resumen, la prima de una opción se compone de un valor cierto llamado valor intrínseco y otro más subjetivo que tiene que ver con la probabilidad de que la opción se ejerza o no llamado valor temporal (ver gráficos 5 y 6). GRÁFICO 5 VALOR TEÓRICO CALL@100 30 25 20 15 Prima Call VI VT 10 5 75 77 79 81 83 85 87 89 91 93 95 97 99 101 103 105 107 109 111 113 115 117 119 121 123 125 0 91 4 SENSIBILIDADES DE LAS OPCIONES Para la toma de posiciones en opciones es conveniente conocer cómo afectan al precio de una opción los movimientos en el precio del activo subyacente, volatilidad, tiempo a vencimiento, tipos de interés y dividendos tal y como hemos visto en el capítulo anterior (ver cuadro 1). Pero no sólo es necesario saber si el efecto beneficia o perjudica a la cartera. También es fundamental poder cuantificarlo. Para ello utilizaremos las sensibilidades (también llamadas Griegas). CUADRO 1 RESUMEN DE MOVIMIENTOS EN PARÁMETROS QUE AFECTAN A LA VALORACIÓN DE OPCIONES Subyacente Movimiento s t t s P.Ejercicio s t s t s t s s s t t t Temp. Vto. t t t Dividendos s t s t s t s Suby.Contado s t s Suby.futuro t t t Suby.Contado t s t Suby.futuro s s Volatilidad T.Interés Call s Put t 127 OPCIONES Y FUTUROS DE RENTA VARIABLE: MANUAL PRÁCTICO: Por ejemplo, a partir de la siguiente cartera de Telefónica: CUADRO 2 Subyacente Telefónica C/V c Activo Call PE 17 Vencimiento 18/06/2010 Volumen 100 Precio Mercado 1,06 euros Telefónica v Telefónica c Call 18 18/06/2010 125 0,52 euros Put 17,5 18/06/2010 75 Telefónica 0,51 euros v Put 18,5 18/06/2010 90 Telefónica 1,09 euros c Put 19 18/06/2010 50 1,46 euros ¿Podríamos responder a las siguientes preguntas básicas?: z ¿Se trata de una cartera alcista o bajista? z ¿Cuánto ganamos/perdemos ante movimientos de un tick en el activo subyacente? z ¿Cuánto ganamos/perdemos ante movimientos en la volatilidad? z ¿Cuánto ganamos/perdemos por el paso de un día? Claramente, a simple vista estas y otras preguntas no podemos responderlas. Por ello, los operadores de los mercados de opciones se ayudan de las sensibilidades, de modo que al final de este capítulo volveremos a analizar la cartera y responderemos a esas preguntas sin la menor dificultad. A partir de los diferentes parámetros que afectan al precio de una opción, se definen las siguientes sensibilidades: z Delta: variación de la prima ante la variación de un tick en el activo subyacente. z Gamma: variación de delta ante la variación de un tick en el activo subyacente (algunos operadores prefieren expresar en sus carteras gamma como la variación de delta ante la variación de un 1% en el activo subyacente). z Vega: variación de la prima ante la variación de un 1% en la volatilidad. z Theta: variación de la prima ante el paso de un día. z Rho: variación de la prima ante la variación de un 1% en el tipo de interés. Es importante destacar cómo las sensibilidades delta y gamma se definen a partir de la variación de un tick en el activo subyacente, ya que dependiendo del tipo de producto de que se trate, este concepto varía. DELTA Indica cuánto varía la prima de una opción ante movimientos de un tick en el activo subyacente. Matemáticamente es la derivada de la prima respecto del activo subyacente o, lo que es lo mismo, la pendiente del valor teórico de la opción: Δ = δP δAS 128 SENSIBILIDADES DE LAS OPCIONES 4 Las opciones no son productos lineales. Por lo tanto, su precio fluctúa de distinta manera en función de dónde se encuentre el activo subyacente (ver gráfico 1 y cuadro 3). GRÁFICO 1 VALOR TEÓRICO CALL 14.500 1.600 1.400 Valor teórico Call 1.200 1.000 800 600 400 200 16.000 15.800 15.600 15.400 15.200 15.000 14.800 14.600 14.400 14.200 14.000 13.800 13.600 13.400 13.200 13.000 0 Activo subyacente CUADRO 3 Call IBEX 35 PE 14.500 Incremento del AS De 13.000 a 14.000 = 1.000 ptos. Incremento de la Prima De 8 a 134 (aprox.)= 126 ptos. De 14.000 a 15.000 = 1.000 ptos. De 134 a 641 (aprox.) = 507 ptos. De 15.000 a 16.000 = 1.000 ptos. De 641 a 1510 (aprox.) = 869 ptos. Como podemos observar en el cuadro anterior, para una opción call sobre Ibex con precio de ejercicio 14.500, incrementos equivalentes en el activo subyacente no provocan el mismo incremento en la prima. Así, cuando la opción está OTM (out of the money) un incremento de 1.000 puntos en el activo subyacente apenas provoca movimiento en el precio de la opción. En cambio, cuando la opción está ATM (at the money), el aumento de la prima es aproximadamente la mitad. Por último, cuando la opción está ITM (in the money) los incrementos en el activo subyacente y prima son aproximadamente los mismos. A partir de esta información se concluye, asombrosamente, que las opciones tienen menor riesgo direccional que el activo subyacente, ya que si no están muy ITM, las primas siempre variarán menos que éste. Un aumento del activo subyacente provoca un incremento en el valor del call, por lo que delta del valor teórico de un call se define con signo positivo (pendiente positiva). Sin embargo, en el caso de un put activo subyacente y prima se mueven en sentido contrario, por lo que delta del valor teórico de un put se define con signo negativo (pendiente negativa). Teniendo en cuenta que delta de las opciones varía entre 0 y 1 (en valor absoluto) representamos en los gráficos 2 y 3 la información anterior: 129 OPCIONES Y FUTUROS DE RENTA VARIABLE: MANUAL PRÁCTICO: CUADRO 4 DELTA DE CALL Y PUT CALL OTM 0 ATM 0,5 ITM 1 0 -0,5 -1 PUT GRÁFICO 2 VALOR TEÓRICO CALL 14500 1.600 1.400 Valor teórico Call 1.200 1.000 800 600 400 Δ=1 Δ=0 200 15.000 15.200 15.400 15.600 15.800 16.000 15.000 15.200 15.400 15.600 15.800 16.000 14.800 14.600 14.400 14.200 14.000 13.800 13.600 13.400 13.200 13.000 0 Activo subyacente DELTA CALL 14500 1,0 0,9 0,8 Delta 0,7 0,6 0,5 0,4 0,3 0,2 0,1 14.800 14.600 14.400 14.200 14.000 13.800 13.600 13.400 13.200 13.000 0 Activo subyacente En el ejemplo numérico en el cuadro 5, observamos cómo el movimiento de un tick del activo subyacente provoca una variación en la prima de la opción exactamente en la cuantía indicada por su delta. Por lo tanto, la definición de delta nos permite cuantificar el efecto que va a tener una variación en el activo subyacente sobre el precio de una opción. Este efecto va a ser diferente en función de que 130 SENSIBILIDADES DE LAS OPCIONES 4 GRÁFICO 3 VALOR TEÓRICO PUT 14500 1.600 1.400 Valor teórico Call 1.200 Δ=1 1.000 800 600 Δ=0 400 200 15.800 16.000 15.800 16.000 15.400 15.400 15.600 15.200 15.200 15.600 15.000 15.000 14.800 14.600 14.400 14.200 14.000 13.800 13.600 13.400 13.200 13.000 0 Activo subyacente DELTA PUT 14500 0 -0,1 -0,2 -0,4 -0,5 -0,6 -0,7 -0,8 -0,9 14.800 14.600 14.400 14.200 14.000 13.800 13.600 13.400 13.200 -1,0 13.000 Delta -0,3 Activo subyacente CUADRO 5 Cotización Subyacente Precio de ejercicio Tipo de interés Días a vencimiento Dividendo Continuo Volatilidad 14.900 14.950 5% 30 5% 30% 14.901 14.950 5% 30 5% 30% Call Prima Call Delta Put Prima PutDelta 485,34 0,50 535,13 -0,50 485,84 534,64 131 5 ESTRATEGIAS OPCIONES ESTRATEGIAS SIMPLES CON OPCIONES: COBERTURA ESTÁTICA CON PUT A la hora de abordar esta tipología de estrategias, es necesario anticipar que la calificación de "estática" es engañosa. Efectivamente, en el mundo de las opciones no hay nada estático, ya que se trata de una herramienta que precisamente lo que aporta es una gran flexibilidad en la gestión; mediante la operativa con opciones se pueden crear sintéticamente distintos perfiles y adaptar de forma instantánea la cartera a unas determinadas expectativas sobre el mercado. De hecho, como veremos a continuación, cubrir una cartera de acciones con compra de put supone convertir la posición resultante en un call sintético. El adjetivo de "estática" se debe a la contraposición de este tipo de estrategias frente a las coberturas dinámicas, también llamadas delta neutral, cuyo objetivo, como ya se ha explicado en anteriormente, es completamente distinto. A diferencia las coberturas con futuros ya analizadas, las coberturas con opciones no eliminan las expectativas de movimiento del activo subyacente, sino que las modifican añadiendo un elemento, la volatilidad. En función precisamente de esa volatilidad y de las expectativas que queramos incorporar a la cartera, escogeremos distintos tipos de coberturas o combinaciones de opciones. Las posibilidades son enormes, esa es la virtud de las opciones, pero también es su pecado, ya que es difícil seleccionar, entre tantas alternativas, cuál es la mejor para la cartera. Antes de realizar la cobertura, tenemos que tener claras las expectativas que queremos incorporar, para ello deberíamos hacernos unas cuantas preguntas: z En cuanto al activo subyacente: ¿va a caer o no?, ¿mucho o solo es una corrección?, ¿durante cuánto tiempo?, ¿el valor está bajista, alcista o lateral?, ¿hay algún soporte o resistencia próximos sobre el que basar mis decisiones?, ¿merece la pena cubrir o deshago la posición 157 OPCIONES Y FUTUROS DE RENTA VARIABLE: MANUAL PRÁCTICO: y busco otras inversiones?, ¿cuánto estoy dispuesto a perder? ¿cuánto quiero ganar y en cuanto tiempo?, etc. z En cuanto a la volatilidad: ¿está cara o barata?, ¿históricamente estamos bajos o altos?, ¿cómo está la volatilidad implícita con respecto a la realizada?, ¿cómo estaba la volatilidad implícita respecto a la realizada hace un mes?, ¿cómo está la volatilidad del valor respecto a la de su sector?, ¿y con respecto a la del mercado?, etc. Una vez respondidas a estas y otras muchas preguntas, o incluso si no somos capaces de responder a todas ellas, podremos determinar si conviene realizar una cobertura comprando put, vendiendo call, comprando putspread, con túnel bajista, etc. Sabremos también qué precio de ejercicio y qué vencimiento es el que mejor se adecúa a nuestros propósitos. En primer lugar vamos a analizar la cobertura con compra de put, mientras que el resto de estrategias serán analizadas con posterioridad. Pongamos un ejemplo sencillo: partimos una cartera compuesta por 1.000 acciones de Telefónica. Hemos comprado las acciones con un dinero que teníamos ahorrado y que queremos invertir durante 3 ó 4 meses para obtener una rentabilidad adicional. Conocemos perfectamente el riesgo de comprar acciones, que es precisamente el de caída de su precio y estamos dispuestos a asumirlo, pero no nos gustaría perder mucho dinero porque lo necesitaremos en un futuro. Sin embargo, sí que nos gustaría beneficiarnos de una posible subida. Si se nos planteara la siguiente posibilidad: "su inversión tiene ahora mismo un valor de 17.000€ (TEF cotiza a 17,00), si usted paga 590€, se asegura que hasta junio no puede perder más de 590€ y sin embargo puede ganar todo lo que suba Telefónica". En las circunstancias CUADRO 1 TELEFONICA FUTUROS 16/04/2010 Compra Vencimiento 18-jun-10 Tipo Entrega Vol. 177 Venta Precio 16,98 Precio 17,24 Vol. 100 Ult. 17 Vol. 7.051 Volumen Total Máx. 17,39 Min. 16,97 Ant. 17,43 Hora 17:34 7.051 OPCIONES EUROPEAS 16/04/2010 CALL Compra Hora 17:22 Vol. 0 17:32 0 17:33 10 17:31 17:33 17:19 25 16:39 0 15:56 Vol. Precio 30 1,17 Vencimiento Compra Venta Precio 1,26 Vol. 100 Prec. Ejerc. 18 jun - 16,00 Vol. 100 Precio 0,21 Precio 0,26 Vol. 100 Últ. Vol. 0 Hora 17:32 0,3 10 17:31 0 17:33 100 0,85 0,91 100 18 jun - 16,50 100 0,34 0,39 100 100 0,55 0,60 100 18 jun - 17,00 100 0,54 0,59 100 0 100 0,32 0,37 100 18 jun - 17,50 100 0,80 0,86 100 0 17:32 0 100 0,16 0,21 100 18 jun - 18,00 100 1,14 1,22 100 0 17:34 0 80 158 Últ. PUT Venta 0,66 0,14 100 0,07 0,12 100 18 jun - 18,50 100 1,54 1,62 100 0 17:34 100 0,02 0,10 100 18 jun - 19,00 100 1,98 2,08 100 0 17:34 0,10 100 18 jun - 19,50 Volumen Total 20 ESTRATEGIAS OPCIONES 5 expuestas anteriormente, probablemente diríamos que sí, ya que esta alternativa se adapta a nuestras necesidades. Nos están ofreciendo un seguro para nuestra inversión. Se trata de una estrategia tan sencilla como la compra de un put. Tal y como se puede observar en el cuadro 1, el put de junio 17,00 cotiza a 0,59 (euros por acción). Si tenemos acciones y put compradas en la misma proporción, la posición resultante sintéticamente es call comprado (ver gráfico 1). GRÁFICO 1 COBERTURA CON C/ PUT ATM 2.500 2.000 1.500 AS=17 Beneficio/pérdida 1.000 PE=17 500 0 -500 Prima=0,59 -1.000 -1.500 C/ PUT AS Total Break Even=17,59 -2.000 19,0 18,8 18,6 18,4 18,2 18,0 17,8 17,6 17,4 17,2 17,0 16,8 16,6 16,4 16,2 16,0 15,8 15,6 15,4 15,2 15,0 -2.500 Activo subyacente Según la paridad call-putI, sin tener en cuenta tipos de interés: K+C=S+P17,00+C=17,00+0,59C=0,59 El call sintético resultante tiene un precio de 0,59, por lo que podemos deducir que esta estrategia tiene en el vencimiento de junio: z Máxima pérdida = 590 € z Máximo beneficio = ilimitado, todo lo que suba el activo subyacente. z Punto de Break Even = 17,59 = 17+0,59. (PE+ call sintético o activo subyacente + put, que en este caso resultan ser los mismos números al coincidir activo subyacente y precio de ejercicio). Esta estrategia nos permite beneficiarnos de subidas en el activo subyacente, pero también hace posible ejercer el put en el caso de la evolución desfavorable de los precios que supone una caída de la cotización. Por lo tanto, esta técnica se llevará a cabo cuando esperemos una alta volatilidad en dos sentidos: z Volatilidad del activo subyacente: esperamos que el activo subyacente en la fecha de vencimiento cotice muy por encima o muy por debajo de su nivel actual. z Volatilidad implícita: esperamos que la volatilidad con la que cotizan las opciones aumente y con ella el valor de nuestras opciones. 159 OPCIONES Y FUTUROS DE RENTA VARIABLE: MANUAL PRÁCTICO: En función de cuánta volatilidad esperemos tanto en el activo subyacente como en las opciones, el inversor podrá elegir opciones a más corto o a más largo plazo y opciones ITM, ATM o OTM. En este aspecto, no se puede valorar qué tipo de cobertura con put es mejor, ya que depende de las expectativas de cada inversor. En cuanto al plazo, recordemos: z Opciones a corto plazo: más baratas, menor vega y mayor theta. Esto significa que necesitamos menos movimiento del activo subyacente para recuperar la inversión, pero aumentos en la volatilidad implícita nos harán ganar poco dinero. Por otro lado, el paso del tiempo nos afecta mucho si tenemos la intención de deshacernos de la posición antes del vencimiento. z Opciones a largo plazo: más caras, mayor vega y menor theta. Necesitaremos un mayor movimiento del activo subyacente debido a su mayor precio, pero aumentos en la volatilidad implícita nos harán ganar más dinero. El paso de tiempo, de momento, afectará poco a la posición. En cuanto al precio de ejercicio de la put: z Con una put ATM (17,00), tendremos un call sintético ATM. Tal y como hemos mostrado en el ejemplo anterior, el coste de la cobertura sería 590€ (3,47%), el punto de break even por tanto es 17,59€ y la máxima pérdida es de 590€ (3,47%). z Con una Put OTM (16,00), tendremos un call sintético ITM. El coste de la cobertura es 260€ (1,53%), por lo tanto, TEF tendría que subir solo hasta 17,26€ para recuperar el coste de la cobertura. El inconveniente es que solo podremos ejercer el put por debajo de 16,00€. La máxima pérdida es de 1.260€ (7,41%) (Ver gráfico 2). z Con un Put ITM (18,00), tendremos un call sintético OTM. El coste de la cobertura es 1.220 euros (7,17%). Por lo tanto, TEF tendría que subir hasta 18,22€ para que recuperemos el coste de la cobertura, sin embargo podremos ejercer el put siempre que TEF esté por debajo de 18,00€. La máxima pérdida será 220€ (1,30%) (ver gráfico 3). GRÁFICO 2 COBERTURA CON C/ PUT OTM 2.500 2.000 PE=16 1.500 AS=17 Beneficio/pérdida 1.000 500 0 -500 Prima=0,26 -1.000 -1.500 C/ PUT AS Total Break Even=17,26 -2.000 Activo subyacente 160 19,0 18,8 18,6 18,4 18,2 18,0 17,8 17,6 17,4 17,2 17,0 16,8 16,6 16,4 16,2 16,0 15,8 15,6 15,4 15,2 15,0 -2.500 ESTRATEGIAS OPCIONES 5 GRÁFICO 3 COBERTURA CON C/ PUT ITM 2.500 2.000 1.500 PE=18 AS=17 Beneficio/pérdida 1.000 500 0 -500 -1.000 -1.500 Break Even=18,22 C/ PUT AS Total -2.000 Prima=1,22 19,0 18,8 18,6 18,4 18,2 18,0 17,8 17,6 17,4 17,2 17,0 16,8 16,6 16,4 16,2 16,0 15,8 15,6 15,4 15,2 15,0 -2.500 Activo subyacente Por lo tanto, una vez tomada la decisión de llevar a cabo una estrategia de cobertura de una posición larga en acciones mediante la compra de put, la selección del precio de ejercicio de la opción a comprar determinará el perfil resultante de la cobertura. Así, cuanto menor sea el precio de ejercicio de la put, menor será la prima a desembolsar, pero mayor será la pérdida máxima asumida. Por otro lado, cuanto mayor sea el precio de ejercicio de la put, mayor será la prima a desembolsar, pero menor será la pérdida máxima asumida. ESTRATEGIAS SIMPLES CON OPCIONES: COBERTURA ESTÁTICA CON CALL En esta ocasión vamos a estudiar la combinación de una compra de acciones con una venta de call que, como ya sabemos, sintéticamente es una venta de put. Podemos pensar que convertir una posición que tiene beneficios y pérdidas ilimitadas en una posición con beneficios limitados y pérdidas ilimitadas no es una operación de cobertura. Sin embargo, a continuación comentaremos las situaciones en las que esta estrategia podría resultar interesante y sus características. Utilicemos el mismo ejemplo que en el apartado anterior, dónde expusimos la cobertura con compra de put, con el propósito de que podamos comparar las dos alternativas. Supongamos que hemos comprado 1.000 acciones de Telefónica pensando que la cotización va a subir en los próximos meses. Sin embargo va pasando el tiempo y las acciones no terminan de "despegar". Por otro lado tampoco se ha producido una caída de la cotización, simplemente el valor está teniendo un comportamiento lateral en un rango estrecho que nos deja muy poco margen y no es la rentabilidad que estábamos buscando. Nos hemos equivocado. En esta situación, podemos hacer dos cosas: la primera es vender las acciones y replantear nuestra inversión y la segunda es intentar obtener una rentabilidad aprovechándonos de la 161 6 MODIFICACIÓN DEL PERFIL: ANÁLISIS DE SENSIBILIDAD La principal ventaja que le otorga a un gestor controlar perfectamente el uso de las opciones es la flexibilidad que éstas le aportan en la gestión de su cartera. Tanto el mercado como las expectativas del gestor van evolucionando y las opciones permiten ir adaptando en todo momento la cartera a dichas expectativas. Con un pequeño cambio se puede cubrir la cartera, transformarla de alcista a bajista o adaptarla a un entorno de alta o baja volatilidad. La búsqueda de estrategias que maximicen el beneficio mientras se es capaz de controlar el riesgo asociado a la posición será la máxima preocupación de un gestor, por ello las opciones serán para él un gran aliado. Explicaremos cómo podemos hacer evolucionar una posición para adaptarla a unas expectativas tanto de movimiento en el activo subyacente como de variación en volatilidad. Sin embargo, antes de plantear una modificación es necesario analizar la posición, saber qué potencial tiene, cuáles son sus riesgos y cómo se debe modificar ante un cambio en las condiciones del mercado. Las “”griegas”” nos van a ayudar mucho en esta tarea. Sin embargo, mirando a estas sensibilidades es muy difícil captar todos los riesgos que entraña una posición y ver cómo evolucionan. Muchos traders encuentran más fácil interpretar la información que otorgan los gráficos, por ello será muy útil graficar la posición suponiendo una serie de cambios en las condiciones del mercado. Veamos un sencillo ejemplo. 215 OPCIONES Y FUTUROS DE RENTA VARIABLE: MANUAL PRÁCTICO: C U A D R O 1 (1) Precio AS 99 Volatilidad 20% Días a Vto 50 T. Interés 6% Dividendo 0% Compra 10 Call Jun @ 95 Venta 30 Call Jun @ 105 Precio 5,85 Delta 0,7596 Gamma 0,0424 Theta -0,0341 Vega 0,1139 1,10 0,2588 0,0441 -0,0277 0,1185 Prima Neta 25,45 Delta Total -0,1693 Gamma Total -0,9003 Theta Total 0,4904 Vega Total -2,4175 Como se puede observar en el cuadro 1, la posición de nuestro ejemplo, un Ratio Call Spread, se tomará cuando se cree que la volatilidad es demasiado alta y que bajará: mientras que delta es prácticamente neutral, gamma y vega son negativas y theta es positiva. Gamma negativa nos indica que movimientos fuertes del activo subyacente perjudicarán la posición, ya que un movimiento al alza hará que la posición sea bajista y un movimiento a la baja hará que sea alcista, justo lo contrario de lo que debería ser para obtener un beneficio. Si se quisiera mantener la posición delta neutral, habría que vender 0,9 acciones si el subyacente cae un punto (o cualquier otra posición delta negativa que neutralice el movimiento) y comprar 0,9 acciones cuando el subyacente suba otro punto (o cualquier otra posición delta positiva)(2). Un Ratio Vertical Spread, además, tiene theta positiva por lo que el paso del tiempo favorece la posición. Tal y como podemos observar en el gráfico 1, según disminuye el tiempo a vencimiento su valor aumenta. GRÁFICO 1 VALOR TEÓRICO RATIO CALL SPREAD CON RESPECTO AL PASO DEL TIEMPO Valor teórico 50/100 100 50 0 75 -50 78 81 84 87 90 93 96 99 102 105108111 -100 114117 120 123 50 -150 -200 -250 -300 -350 Activo subyacente en % 216 0/50 42 34 26 18 10 2 -50/0 -100/-50 -150/-100 -200/-150 -250/-200 -300/-250 Dias a vencimiento -350/-300 MODIFICACIÓN DEL PERFIL: ANÁLISIS DE SENSIBILIDAD 6 No solo el beneficio potencial de la posición cambia cuando pasa el tiempo, también lo hacen los riesgos asociados. Como podemos observar en el gráfico 2, el paso del tiempo hace que las deltas se alejen de 0,5; para la opción dentro del dinero su delta tiende a 1 mientras que la opción que está fuera del dinero tiende a 0. El efecto neto es que si el activo subyacente está por debajo de 105, el paso del tiempo hará que delta aumente. Sin embargo, si el precio del activo está por encima de 105 las dos call estarán dentro del dinero y sus deltas tenderán hacia 1 haciendo que la delta total sea cada día que pase más negativa. Gamma también cambia con el paso del tiempo. Las opciones ATM siempre tienen gamma máxima y ésta aumenta muy rápidamente con el paso del tiempo. GRÁFICO 2 DELTA Y GAMMA CON RESPECTO AL PASO DEL TIEMPO 5/10 10,0 6 5,0 -5,0 -10,0 28 75 77 79 81 83 85 87 89 91 93 95 97 99 101 103 105 107 109 111 113 115 117 119 121 123 125 Delta 0,0 17 0/5 -5/0 39 50 -10/-5 -15/-10 -15,0 -20/-15 -20,0 Activo subyacente en % Dias a vencimiento 217 OPCIONES Y FUTUROS DE RENTA VARIABLE: MANUAL PRÁCTICO: En el gráfico 3 vemos cómo el paso del tiempo afecta de manera muy distinta a theta y a vega. Theta y gamma son de signo contrario pero tienen una gran correlación, por ello, lo explicado para gamma es extensible a theta. Sin embargo vega, que es muy grande cuando queda mucho tiempo a vencimiento, decrece con el paso de los días, afectando muy poco cuando se aproxima el vencimiento. GRÁFICO 3 THETA Y VEGA CON RESPECTO AL PASO DEL TIEMPO 6/7 Theta dias a vencimiento 7,0 6,0 5,0 2 4,0 10 3,0 18 2,0 26 1,0 34 0,0 42 -1,0 75 77 79 81 83 85 87 89 91 93 95 97 99 50 101 103 105 107 109 111 113 115 117 119 121 123 125 -2,0 Activo subyacente en % -3,0 Vega 75 78 81 84 87 90 93 96 99 102 105 108 111 114 117 120 123 50 46 42 38 34 30 26 22 18 14 10 6 2 0,0 4/5 3/4 2/3 1/2 0/1 -1/0 -2/-1 0/1 1,0 -1,0 5/6 -2,0 -3,0 -4,0 -1/0 -2/-1 -3/-2 -4/-3 -5,0 -5/-4 Activo subyacente en % Dias a vencimiento Como vega es negativa, cualquier aumento en volatilidad implícita perjudicará a la posición y una disminución le beneficiará. Tal y como se muestra en el gráfico 4, el valor teórico de la posición varía con cambios en volatilidad, teniendo en cuenta que a diferencia del efecto de paso del tiempo, esta variable puede tanto aumentar como disminuir. Adicionalmente, el cambio en la volatilidad implícita también afectará a las sensibilidades, llevándose las deltas lejos de 0,5 cuando cae o arrastrándolas hacia ese punto cuando aumenta. Por lo tanto, si cae la volatilidad delta se vuelve positivo y si aumenta negativo. Este hecho se pone de manifiesto claramente en el gráfico 4 donde, para un nivel del activo subyacente en 99, ante una caída de 218 MODIFICACIÓN DEL PERFIL: ANÁLISIS DE SENSIBILIDAD 6 la volatilidad la pendiente se vuelve positiva mientras que ante un aumento de la volatilidad la pendiente se torna negativa. GRÁFICO 4 VALOR TEÓRICO RATIO CALL SPREAD CON RESPECTO AL MOVIMIENTO DE LA VOLATILIDAD Valor teórico 50/100 100 50 46% 0 38% 30% -50 75 78 81 84 87 90 93 96 22% -100 99 102105 14% 108 111 114 -150 117 120 123 6% -200 -250 -300 -350 -400 Volatilidad Activo subyacente en % 0/50 -50/0 -100/-50 -150/-100 -200/-150 -250/-200 -300/-250 -350/-300 -400/-350 El cuadro 2 resume y cuantifica todo lo visto anteriormente. Es una matriz de tensión, lo que significa que estresa el movimiento del subyacente y de la volatilidad. En nuestro caso lo hemos hecho por tramos destacando en negrita la situación actual. Por ejemplo, si sube el activo subyacente un 10% (de 99 a 108,9) pero cae la volatilidad un 10% (de 20% a 18%), la posición perdería 53,04€, la delta se volvería muy negativa y el resto de los riesgos aumentarían significativamente. CUADRO 2 MATRIZ DE TENSIÓN 89,1 22% 20% 18% 10% 0% -110% Bº/Pª -110% -17,05 € 94,05 99 103,95 108,9 -55% -7,92 € 0% -4,94 € 5% -22,26 € 10% -67,84 € Delta 1,6800 1,6838 -1,0033 -6,2794 -12,0123 Gamma 0,1619 -0,2299 -0,8530 -1,1973 -1,0483 Theta -0,1084 0,1117 0,5740 0,9656 1,0324 Vega 0,3874 -0,6129 -2,5195 -3,8988 -3,7468 Bº/Pª -18,00 € -6,99 € - € -14,36 € -60,38 € Delta 1,7869 2,3442 -0,1694 -6,0092 -12,4059 Gamma 0,2545 -0,1277 -0,9003 -1,3509 -1,1412 Theta -0,1357 0,0287 0,4905 0,9043 0,9579 Vega 0,5535 -0,3094 -2,4176 -3,9991 -3,7080 Bº/Pª - 19,23 € -6,70 € 4,71 € -6,25 € -53,04 € Delta 1,7870 3,0052 0,7978 -5,7273 -12,9163 -1,2393 Gamma 0,3452 0,0133 -0,9460 -1,5434 Theta -0,1468 -0,0486 0,4035 0,8412 0,8790 Vega 0,6758 0,0289 -2,2861 -4,1123 -3,6238 219