Valores extremos Concavidad
Anuncio

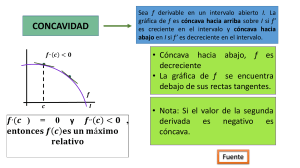
Valores extremos Valor crítico (c) f'(c) = 0 ó f'(c) no está definida Criterio de la primera derivada Se hallan los valores críticos y se evalúan los intervalos formados por éstos para identificar el ) signo de ( ( ). Punto crítico f(c) Evaluamos la función dada en los valores críticos que pertenezcan al Dominio de f. Intervalo cerrado [ a, b ] Hallamos ; ( ) ( ) ( ) Intervalo abierto ( a, b ) Hallamos los puntos críticos ( ) El valor mayor es un máximo absoluto. El valor menor es un mínimo absoluto. ( Valor a la izquierda de c El valor mayor es un máximo relatito. El valor menor es un mínimo relativo. ) ( ) Valor a la derecha de c Comportamiento de f(x) Valores extremos Si ( ) , entonces f(x) es creciente en ese intervalo. ( ) ( ) Entonces c, es un máximo relativo Si ( ) , entonces f(x) es decreciente en ese intervalo. ( ) ( ) Entonces c, es un mínimo relativo Concavidad Criterio de la Segunda Derivada Criterio de la Primera Derivada La función f(x), tiene un punto de inflexión en aquellos valores c. donde ( ) ó sea no definida. ( ) es creciente en el intervalo (a,b) entonces la función f(x) es Si cóncava hacia arriba en ese intervalo. ( ( ) ( ) ) ( ) ( ) ( ( ) es decreciente en el intervalo (a,b) entonces la función f(x) Si es cóncava hacia abajo en ese intervalo. ) en ese intervalo. en ese intervalo.