Una fábrica de vestidos encuentra que el costo
Anuncio

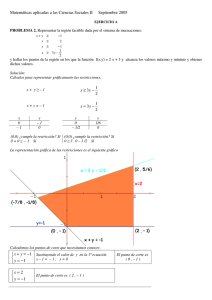
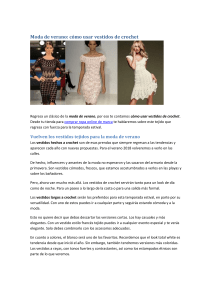
Una fábrica de vestidos encuentra que el costo para producir 10 piezas es $40 y el costo para 20 piezas es $70. Si el costo está relacionado de manera lineal con la producción: 1. Determine la ecuación costo - producción. 2. ¿Cuál es el costo total de producir 35 vestidos? 3. ¿Cuál es el costo fijo, costo variable y costo promedio de producir 35 vestidos? 1. Determine la ecuación costo - producción. Costo ($) 100 (20,70) (10, 40) 50 5 10 15 Producción (piezas) 20 Como el costo es diréctamente proporcional a la producción y la relación entre ambas variables es lineal, podemos describirla con la ecuación: y = b + mx Para saber cuanto vale m (pendiente) usamos la siguiente expresión: Sustituyendo los 2 valores de la grafica tenemos que: m= 70 - 40 = 20 - 10 30 =3 10 Para saber cuanto vale b (intercepto) usamos la siguiente expresión: b = y - mx Y sustituyendo los valores del 2do. punto de la grafica tenemos que: b = 70 - 3 (20) = 70 - 60 = 10 La ecuación de la recta es: Y = 10 + 3X b = 10 Costo ($) m=3 100 (20,70) (10, 40) 50 (0, 10) 5 10 15 Producción (piezas) Producir cada vestido adicional cuesta $3 más. 20 2.- ¿Cuál es el costo total de producir 35 vestidos? Y = 10 + 3X Y = 10 + 3(35) = $115 3.- ¿Cuál es el costo fijo, costo variable y costo promedio de producir 35 vestidos? Costo fijo = b = 10 Costo variable = mx = 3(35) = $105 Costo promedio = Y = Y= b X 10 35 Y = $3.28 + m + 3