TRIGONOMETRY I Exercise – 1 Q. 1 (b) Given the diameter of
Anuncio

TRIGONOMETRY I
Exercise – 1
Q. 1
(b)
Given the diameter of circular wire = 14 cm.
Therefore length of wire = 14 cm
Hence, required angle
7 180 o
210 o
6
Q. 2
(d)
We have, radians
180
1c
Arc
4 7
Radius
12
6
radian
.
180 o
o
;
c
o
2
2 180
o
24 .
15
15
Q. 3
(a)
Let the angles in degrees be 3 , , , 3
90 o
Sum of the angles 4 360 o
Also greatest angle 3 120 o ,
Hence, 3 120 o 120 o 90 o 30 o 10 o
Hence the angles are 90 o 30 o ,90 o 10 o ,90 o 10 o and
That is, the angles in degrees are
60 o , 80 o , 100
In terms of radians the angles are
o
4 5
3
,
9
,
9
90 o 30 o
and
120
and
2
3
o
.
Q. 4
(b)
We know that the tip of the minute hand makes one complete round in one hour
i.e. 60 minutes since the length of the hand is 10 cm.
the distance moved by its tip in 60 minutes 2 10 cm 20 cm
Hence the distance in 20 minutes
Q. 5
(c)
Required angle =
Q. 6
20
20
20 cm
cm .
60
3
Arc
1
radian
radius 3
.
(b)
Area of sector subtending an angle of radian at centre of a circle of radius r is
Also area of triangle having sides a & b and included angle is
1 2
r
2
1
absin .
2
1
1
1
1
14
Hence required area = 42 4 4 sin 42 4 4 sin
4 2 3
2
Q. 7
4
2
3
2
(c)
n(m 1) (sec cosec ).2 sin . cos
2
4 2
[m 2 1 2 sin . cos ]
3
3
sin cos
.2 sin . cos 2m .
sin . cos
Q. 8
(b)
x sin tan x cos . tan
x
tan
sin
sin cos tan sin cos cos sin
y
Similarly,
x sin
y
sin
Q. 9
sin
sin cos cos sin
;
.
(a)
sec tan 3 sec tan
1
3
sec 2 tan 2 1
5
4
& tan
3
3
4
3
sin & cos
5
5
8
sin cos
5
Hence sec
Q. 10 (c)
(1 sin ) 2
(1 sin 2 )
1 sin
sec tan
cos
.
Q. 11 (c)
sin 6 x cos6 x
3
3
1
1
sin 2 x cos 2 x
2
2
sin 2 x cos 2 x 3sin 2 x cos 2 x sin 2 x cos 2 x
3
1
2
1
1
sin 2 2x
2
3
2
1
1 cos 4x cos 4x
3
3
1 3sin 2 x cos 2 x
Q. 12 (d)
sin x cos x
sin 2 x
24
25
1
5
sin 2 x cos 2 x 2 sin x cos x
cos 2 x
7
25
tan 2 x
24
7
1
25
.
Q. 13 (b)
2
7
24
cos x 1 sin 2 x 1
25
25
tan x
sin x 24
cos x
7
.
Q. 14 (b)
tan sec e x
........(i)
sec tan e x
From (i) and (ii), 2 sec e x e x
Q. 15 (b)
xy
1 sin 1 sin 1 sin 2
1
cos
cos
cos 2
........(ii)
2
cos x
e e x
.
Q. 16 (d)
PQ
2 sin
cos
1 sin cos 1 sin
After solving,
P Q 1.
Q. 17 (c)
= 6(sin6 cos6 ) 9(sin4 cos4 ) 4
= 6[(sin2 cos2 )3 3 sin2 cos2 (sin2 cos2 )] 9[(sin2 cos2 )2 2 sin2 . cos2 ] 4
= 6[1 3 sin2 cos2 ] 9[1 2 sin2 cos2 ] 4 = 6 9 4 1 .
Q. 18 (d)
sin . sin
cos . cos
sin (1 cot ) (1 tan ) cos
=
sin2
cos2
(sin cos ) (cos sin )
2
2
= cos sin cos sin .
(cos sin )
Q. 19 (b)
sin 75 o sin(45 o 30 o ) sin 45 o cos 30 o sin 30 o cos 45 o
1
3 1
1
3 1
2
2
2
2 2
2
.
Q. 20 (c)
5
5
sin
cos sin
4
4
4
4
.
1
1
0
2
2
cos
Q. 21 (a)
tan A cot A ( tan A) ( cot A) 0 .
Q. 22 (a)
3 1
2 2
3 1
2 2
=
1
2
.
Q. 23 (a)
tan cot 2cosec2 tan
cot 2cosec 2 2
8
8
4
Q. 24 (b)
tan cot 2cot 2 tan
cot 2cot 2 3
12
12
6
Q. 25 (b)
Since
sin x sin 2 x 1
sin x 1 sin 2 x cos 2 x
........(i)
From given expression, cos x(cos x 4cos x 6cos x 4cos x 1) = cos8 x(cos2 x 1)4
8
From (i)
8
6
4
2
sin x cos 2 x
sin4 x(sin x 1)4 = (sin2 x sin x)4 1 .
Q. 26 (b)
Given 4 sin 3 cos tan
The given expression is
3
4
sec2
1 tan 2
2
4[1 tan ] 4 (1 tan 2 )
9
16 25
9 28
4 1
16
1
=
.
Q. 27 (d)
o
= 1 tan 12 o tan 147 o = tan(45 o 12 ) tan(180 o 33 o ) tan 33 o ( tan 33 o ) 0 .
1 tan 12
Q. 28 (c)
We know | sin | 1 & | cos | 1 ; So, each sin 1,cos 2 and sin3 must be equal to 1
cos 1 sin 2 cos 3 1 .
Q. 29 (b)
cos A 2cos600o cos A = cosA 2cos(540o 600o )cosA cosA 2cos60o cosA 0
Q. 30 (b)
2(sin 2 A sin 2 B)
2 sin A cos A 2 sin B cos B
=
2 sin( A B) sin( A B)
2 sin(A B). sin(A B)
tan( A B) .
2 sin( A B) cos( A B)
sin 2 A sin 2 B
Q. 31 (c)
cos2 (A B) sin2 B cos(A B)[cos(A B) cos(A B)]
sin2 B cos(A B)cos(A B) sin2 B (cos2 A sin2 B) cos2 A 1 sin2 A
Q. 32 (b)
We have tan
m
m 1
and tan
1
2m 1
m
1
2m 2 m m 1
m
1
2
m
1
tan( )
m
1
2m 2 m 2m 1 m
1
.
(m 1) (2m 1)
2m 2 2m 1
2m 2 2m 1
Hence
1 tan( ) tan
4
4
Trick : As is independent of m, therefore put
Therefore,
tan tan
tan( )
1 tan tan
1 1
tan( ) 2 3 1 ,
1
1
6
Hence
m 1,
then tan
1
2
and tan
1
3
.
(Also check for other values of m)
4
Q. 33 (d)
Given that tan cot a
…….(i)
and
sin cos b
…….(ii)
Now, (b 2 1) 2 (a 2 4 ) {(sin cos )2 1} 2 {tan cot )2 4}
1
1
[1 sin 2 1]2 [tan 2 cot 2 2 4 ] sin2 2 (cosec2 sec2 ) 4 sin2 cos 2 2
4
2
sin cos
Trick : Obviously the value of expression (b 2 1) 2 (a 2 4 ) is independent of , therefore put any suitable
value of . Let 45 o , we get a 0 , b 2 so that [(
Q. 34 (c)
sin(2 A B) 5
sin B
1
by componendo and Dividendo,
2 )2 1]2 (0 2 4 ) 4
.
sin( 2 A B) sin B 5 1
sin( 2 A B) sin B 5 1
2 sin( A B). cos A 6
2 cos( A B). sin A 4
tan( A B) 3
.
tan A
2
Q. 35 (c)
sin 80o sin170o
sin 70 o cos 40 o
o
o
cos10 cos100
cos 70 o sin 40 o
=
sin 70 o sin 50 o
2 sin 60 o cos 10 o
o
o
sin 20 sin 40
2 sin 30 o cos( 10 o )
o
= sin 60 o 3 . 2 3 .
sin 30
2
1
Q. 36 (d)
sin133o sin 241o sin191o sin155o sin 47 o sin 61 o (sin 11 o sin 25 o )
= 2 sin 54 o. cos 7o 2 sin 18 o cos 7o
= 2 cos 7 o (sin 54 o sin 18 o ) = 2 cos 7o.2 cos 36 o. sin 18 o = 4 . cos 7 o. 5 1 . 5 1 cos 7 o .
4
4
Q. 37 (b)
cos10 o sin10 o 1 tan 10 o
tan 35 o tan(90 o 35 o ) = cot 55 o
cos10 o sin10 o 1 tan 10 o
Q. 38
.
(d)
2 A {( A B) ( A B)} tan 2 A
tan( A B) tan( A B)
1 tan( A B). tan( A B)
tan 2A 1 or 2A
Q. 39 (b)
sin(720o 90o 73o ).cos(720o 13o ) sin 720 73 .sin(720o 180o 13o )
o
= cos 73 o. cos 13 o sin 73 o. sin 13 o
cos(73 o 13 o ) cos 60 o
1
2
.
Q. 40 (b)
cot 70 o 4 cos 70 o
cos 70 o 2 sin140 o
cos 70 o 4 sin 70 o. cos 70 o
o
sin 70
sin 70 o
cos 70 o 2 sin(180 40 o ) sin 20 o sin 40 o sin 40 o
sin 70 o
sin 70 o
2 sin 30 o cos 10 o sin 40 o
sin 80 o sin 40 o 2 sin 60 o cos 20 o
3
o
sin 70
sin 70 o
sin 70 o
Q. 41 (b)
1
1
1
1
2 x 1
1 x
tan tan
2
tan( )
tan( )
1
1
1 tan tan
1
.
1 1 2 x 1
1 x
2
tan( )
2 x 2.2 x x 2 x 1
1 2 x 2.2 x 2.2 x x 2 x
tan( ) 1 tan
Q. 42
(b)
4
4
.
.
4
sin 7 sin 2 sin 7 cos 2 cos 7 sin 2
cos 7 cos 2
cos 7.cos 2
sin 5
sin 5
cos5
cos5
=
2 sin(7 2)cos5
2sin 5.cos5
2 cos7.cos 2.sin 5 2cos7 .cos 2 .sin 5
=
2cos5
2.
cos9 cos5
Q. 43 (d)
3
3
cos ve
2
2 2
4
2
1 cos
cos
2
2
4
cos
5
1
2
4
5
9
3
10
10
.
Q. 44 (c)
Since 2 cos( ) 2 cos2 ( ) 1,
2 sin 2 1 cos 2 cos 2 2 cos( )[2 sin sin cos( )]
cos 2 2 cos( ). cos( ) cos 2 cos 2 cos 2 cos 2
.
Q. 45 (b)
2
1
1
3
1
1 1
1 tan 2 15 1 [tan(45 o 30 o )]2
3
2
o
o 2
2
1 tan 15 1 [tan(45 30 )]
1
1
3
1
1 1
3
3 1
1
= 3 1
3 1
1
3 1
2
2
[ 3 1]2 [ 3 1]2
[ 3 1]2 [ 3 1]2
Trick : cos 2
4 3
3
8
2
1 tan 2
1 tan 2 15 o
3
cos 30 o
2
2
1 tan
1 tan 2 15 o
.
Q. 46 (d)
sin 6 2 sin 3 . cos 3
=
2[3 sin 4 sin 3 ][4 cos 3 3 cos ]
= 24 sin . cos (sin2 cos2 ) 18 sin cos 32 sin3 cos3
= 32 cos5 . sin 32 cos3 . sin 3 sin 2
On comparing, x sin 2
Trick : Put 0 o , then x 0 . So, option (c) and (d) are correct.
Now put 30 o , then x 3 . Therefore, Only option (d) is correct.
2
Q. 47 (b)
Given,
x
1
x
2 cos
........(i)
1
x
On squaring both sides we get, x 2 4 cos 2 x
x
1
4 cos 2 2
x
1
2(2 cos 2 1)
x
2 cos 2
........(ii)
Again squaring both sides,
x2
1
2 4 cos 2 2
x2
x2
x2
1
2 cos 4
x2
1
4 cos 2 2 2 2(2 cos 2 2 1)
x2
......(iii)
Now taking cube of both sides;
3
1
2
x 2 (2 cos 4 )3
x
x6
1
x6
3x 2.
1 2
1
x 2 8 cos3 4
x2
x
1
x6
1
3(2 cos 4 )
x6
x6
1
2(4 cos 3 4 3 cos 4 ) 2 cos 3(4 ) 2 cos 12
x6
= 8 cos3 4 x 6
x6
8 cos 3 4 6 cos 4
.
Q. 48 (c)
For A 133 o ,
A
66 .5 o
2
Hence, 1 sin A sin
and 1 sin A sin
sin
A
A
cos
2
2
A
A
cos
2
2
A
A
cos 0
2
2
......(i)
......(ii)
Subtract (ii) from (i) we get,
2 cos
A
1 sin A 1 sin A
2
Q. 49
.
(b)
2 tan A 3 tan B tan A
3
3
tan B t
2
2
(Let tan B t )
sin 2 B
2t
1 t2
sin 2 B
5 cos 2 B
, cos 2 B
2t
1 t2
1 t2
5
2
1 t
1 t2
1 t2
2t
4 6t 2
t
2 3t 2
Q. 50 (d)
sin A
4
4
tan A
5
3
,
(90 o A 180 o )
tan( A B) .
A
2 ,
tan A
2 A
1 tan
2
2 tan
A
P
2
Let tan
4
2P
3
1 P2
4 P 2 6P 4 0 P
1
2
,2 P
1
2
(impossible)
A
So, P 2 i.e., tan 2.
2
Q. 51 (a)
tan
1
1
, sin
7
10
2
3
tan
1
3
3
4
tan 2
1 3
4 21
tan( 2 ) 7 4
1
3
25
1
28
=
1
1
9
Q. 52 (a)
1 t2
1 t2
1 tan 2
=
1 tan
2
2
( tan
t)
2
= cos(2. ) cos .
2
2
Q. 53 (d)
cos3 4cos3 3cos & sin 3 3sin 4sin 3 cos3 sin 3 4 cos3 sin 3 3 cos sin
cos3 sin 3 4 cos sin 12sin cos cos sin 3 cos sin
3
cos3 sin 3 4 cos sin 12sin cos 3 cos sin
2
cos3 sin 3 1 4sin cos cos sin
3 1
Hence cos sin
1 4sin cos cos sin
18
18
18
18
6
6
2
Q. 54 (a)
tan 2 sec 2
2 tan
1 tan 2
2
1 tan 1 tan 2
Given tan t tan 2 sec 2
Q. 55 (b)
Given, sin 2 sin 2
and cos 2 cos 2
3
2
1
2
.......(i)
.......(ii)
2t
1 t2
2t 1 t 2 (t 1)2
1 t2 1 t2
1 t2
1 t2
=
1t
1t
.
Squaring and adding,
(sin2 2 cos2 2 ) (sin2 2 cos2 2 ) 2[sin 2 . sin 2 cos 2 . cos 2 ]
cos 2 . cos 2 sin 2 . sin 2
1
4
cos(2 2 )
1
4
1 9
4 4
cos2 ( )
Q. 56 (b)
Given tan x
=
b
a
ab
ab
1 tan x
1 tan x
1 tan x
1 tan x
ab
ab
1 b /a
1 b /a
1 b /a
1 b /a
2
1 tan 2 x
Now, multiplying by 1 tan 2 x in N'r and D'r
=
2
1 tan x
2
1 tan 2 x
2
. 1 tan x
2
=
2
cos 2 x . sec x
2 cos x
cos 2 x
.
Q. 57 (b)
We have
x
y
z
(say)
1 2 2
x , y 2, z 2
;
xy yz zx 22 4 2 22 0
Q. 58 (a)
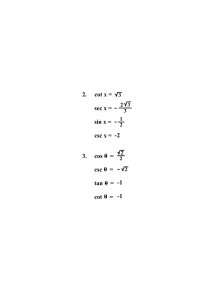
If sec =
2
1
, sin = ± 1 cos2
2
or, cos =
= 1
1
1
=
2
2
But lies in the fourth quadrant in which sin is negative.
sin = –
1
, cosec = – 2
2
tan =
sin
1
tan = –
×
cos
2
2
tan = –1 cot = –1
then,
1 tan θ cosecθ
11 2
=
1 cot θ cosecθ
11 2
Q. 59 (d)
5
8
.
L.H.S., =
2 2 2 2 cos 8
8
2
1 cos8 2 cos2
=
2 2 2(2 cos2 4)
=
2 2 2 cos 4 =
2 2(1 cos 4)
=
2 2(2 cos2 2) =
2 2 cos 2
=
2(1 cos 2) =
2(2 cos2 ) = 2cos .
Q. 60 (a)
As sin θ sin 2 θ sin 3 θ sin θ 1 sin 2 θ cos 2 θ
sin 2 θ 1 sin 2 θ cos 4 θ 1 cos 2 θ 2 cos 2 θ cos 4 θ
2
cos 6 θ 4 cos 4 θ 8cos 2 θ 4
2