0(4 = = = = = = = = = = xxxxx ¿Qué opinas de F ya

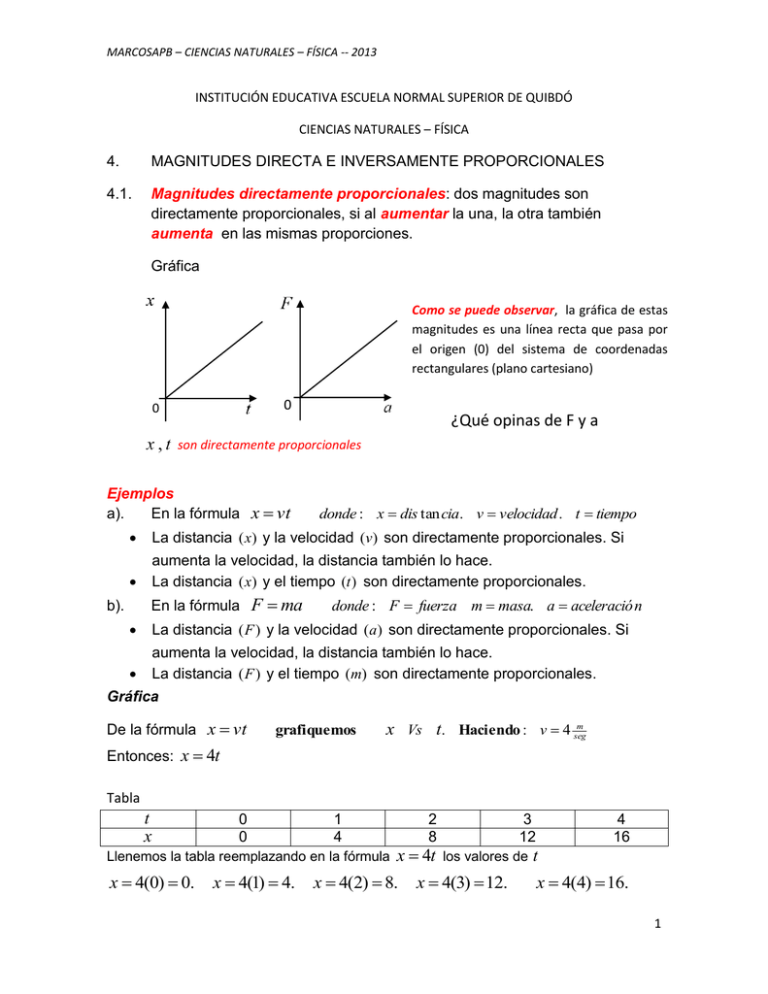
MARCOSAPB – CIENCIAS NATURALES – FÍSICA -- 2013
INSTITUCIÓN EDUCATIVA ESCUELA NORMAL SUPERIOR DE QUIBDÓ
CIENCIAS NATURALES – FÍSICA
4.
MAGNITUDES DIRECTA E INVERSAMENTE PROPORCIONALES
4.1.
Magnitudes directamente proporcionales: dos magnitudes son
directamente proporcionales, si al aumentar la una, la otra también
aumenta en las mismas proporciones.
Gráfica
Como se puede observar, la gráfica de estas
magnitudes es una línea recta que pasa por
el origen (0) del sistema de coordenadas
rectangulares (plano cartesiano)
0
0
¿Qué opinas de F y a
son directamente proporcionales
Ejemplos
a).
En la fórmula x  vt
donde : x  dis tan cia. v  velocidad . t  tiempo

La distancia (x) y la velocidad (v) son directamente proporcionales. Si

aumenta la velocidad, la distancia también lo hace.
La distancia (x) y el tiempo (t ) son directamente proporcionales.
En la fórmula F  ma
b).
donde : F  fuerza m  masa. a  aceleració n

La distancia (F ) y la velocidad (a) son directamente proporcionales. Si

aumenta la velocidad, la distancia también lo hace.
La distancia (F ) y el tiempo (m) son directamente proporcionales.
Gráfica
De la fórmula x  vt
grafiquemos
m
x Vs t. Haciendo : v  4 seg
Entonces: x  4t
Tabla
t
x
0
0
1
4
Llenemos la tabla reemplazando en la fórmula
x  4(0)  0.
x  4(1)  4.
2
8
x  4t
x  4(2)  8.
3
12
los valores de
x  4(3)  12.
4
16
t
x  4(4)  16.
1
MARCOSAPB – CIENCIAS NATURALES – FÍSICA -- 2013
Gráfica de

16

12

8
Como se puede observar, la gráfica de esta fórmula es una línea
recta que pasa por el origen (0) del sistema de coordenadas
rectangulares (plano cartesiano), por eso, son directamente
proporcionales

4
0
2
1
3
4
Las magnitudes directamente proporcionales están ligadas por un cociente
(división) constante, es decir, al dividirlas en todo su recorrido el cociente es el
mismo.
Ejemplo
La tabla muestra algunos valores de dos magnitudes directamente proporcionales
y determinemos la constante de proporcionalidad (cociente constante)
x
0
0

1
6
2
12
3
18
4
24
Dividiendo:

x
:
6
 6.
1
12
 6.
2
18
 6.
3
24
 6 . Como se puede
4
observar, los cocientes son iguales (6), este número recibe el nombre de
constante de proporcionalidad
Los dos primeros valores no se toman por que ambos son ceros (0)
Taller para entregar
Para cada fórmula realice la gráfica indicada
Fórmula
x  vt
F  ma
V  at
P  mV
Haciendo
t  2seg
m  3kg
a  2 segm
2
m  4kg
Reescribiendo la fórmula
x
Gráfica
F
V
x Vs t
F Vs a
V Vs t
P
P Vs V
2
MARCOSAPB – CIENCIAS NATURALES – FÍSICA -- 2013
1.2 Magnitudes inversamente proporcionales: dos magnitudes son
inversamente proporcionales, si al aumentar la una, la otra disminuye en las
mismas proporciones.
Gráfica
Como se puede observar, la gráfica de estas
magnitudes es una parábola, que tiende a
unirse con los ejes, pero que nunca lo hace
0
0
¿Qué opinas de F y a
son inversamente proporcionales
En una fórmula, las magnitudes inversamente proporcionales están
multiplicándose, como: En x  vt ... son vt.
En F  ma ..... son ma.
Ejemplos
x
t
La velocidad (v) y tiempo (t ) son inversamente proporcionales. Si aumenta
De la fórmula x  vt,
a).

despejemos v. Entonces : v 
el tiempo, la velocidad disminuye y viceversa.
F
m
La aceleración (a) y la masa (m) son inversamente proporcionales. Si
aumenta la masa, la aceleración disminuye y viceversa.
V
V  at
despejemos a. Entonces : a 
t
La aceleración (a) y el tiempo (t ) son inversamente proporcionales
De la fórmula F  ma
b).

c).

despejemos a. Entonces : a 
Gráfica
x
De la fórmula x  vt, de donde : v  .
t
10
Entonces: v 
t
Tabla
t
0
1
v
0
10
grafiquemos : v Vs t.
2
5
3
3,3
para x  10m
4
2,5
3
MARCOSAPB – CIENCIAS NATURALES – FÍSICA -- 2013
Llenemos la tabla reemplazando en la fórmula v 
v
10
  N .E.
0
v
10
 10.
1
v
10
los valores de t
t
10
 5.
2
v
10
 3,3.
3
v
10
 2,5
4
Gráfica de
10

Como se puede observar, la gráfica de esta
fórmula es una parábola

5
3,3
2,5

0
1
2
3

4
Las magnitudes inversamente proporcionales están ligadas por un
producto constante, es decir, al multiplicarlas en todo su recorrido el producto es el
mismo.
Ejemplo
La tabla muestra algunos valores de dos magnitudes inversamente proporcionales
y determinemos producto constante
m
a
1
24
Multiplicando:
ma :
1(24)  24.
2
12
2(12)  24.
3
8
4
6
3(8)  24.
4(6)  24 .
Como se puede observar, los productos son iguales (24), este número recibe el
nombre de producto constante
4
MARCOSAPB – CIENCIAS NATURALES – FÍSICA -- 2013
Taller para entregar
Para cada fórmula realice la gráfica indicada
Fórmula
x
t
v
F
a
m
v
a
t
Haciendo
x  20m
F  10N
m
v  10 seg
Reescribiendo la fórmula
Gráfica
t
t
a
a Vs m
a
a Vs t
Vs v
5