Descargar

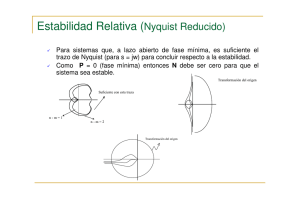
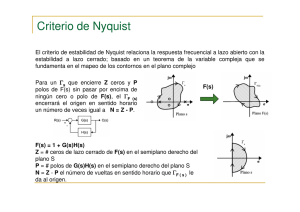
4.6.- CRITERIO DE ESTABILIDAD DE NYQUIST.
Se puede decir que un sistema es estable cuando al ser excitado, la parte transitoria
de su respuesta decae conforme aumenta el tiempo. Para esto, se necesita que las
raíces de su ecuación característica sean reales negativas o complejas con parte real
negativa. Sin embargo, el hecho de que un sistema sea estable, no implica que
sea útil, pues aún cuando su transitorio se haga cero, su duración y características
pueden ser tales que se imponga una modificación en su dinámica. De esta
manera, no basta con establecer de una manera absoluta la estabilidad, es
necesario también cuantificarla.
Para conocer cuan estable es un sistema, se requiere información que la simple
factorización de la ecuación característica o la aplicación de métodos algebraicos
como el de Routh, no pueden proporcionar con exactitud, en cambio se tienen
algunos métodos, basados en la respuesta frecuencial, que son una herramienta
conveniente no solo para determinar las características del comportamiento de los
sistemas, sino también para corregir los efectos no deseados que presenten.
Antes de describir los métodos frecuenciales, se tratarán algunos aspectos
matemáticos, importantes para su discusión.
MAPEO DE CONTORNOS.
Considérese una función racional y univoca F(s) que viene dada — por:
F ( s)
( s z1 )( s z2 ).....( s zm )
( s p1 )(s p2 ).....(s pn )
(n m)
En donde z1 , z2 ,......, zm y p1 , p2 ,......, pn son respectivamente los ceros y los
polos de la función. Como en los polos F(s) no es analítica, esto es, la función o sus
derivadas no existen, se dice que son puntos singulares o singularidades de la
función. Ahora bien, si se traza un contorno arbitrario en el plano "s" como el que se
muestra en la fig. 4.20, tal que no pase por ninguna singularidad de la función y se
valúa a ésta en cada uno de los puntos del contorno, la gráfica de P(s) será también
un camino cerrado, cuyas características están determinadas, por el lugar que
ocupan los ceros y los polos en el plano complejo.
Supóngase que la localización de los ceros y de los polos es la que se muestra en
la fig. 4.21. Para cada valor de s, por ejemplo s0, el valor de la función puede
representarse por un punto, cuya localización en el plano F, viene dada por:
m
F ( s0 )
( s0
zi )
( s0
pj )
i 1
n
j 1
m
F ( s0 )
n
s0
i 1
zi
s0
pj
j 1
Como se puede observar, cada factor contribuye con su módulo y fa se al valor de
la función.
En el plano s, los factores están representados por vectores diferencia, que van de
los ceros y los polos al punto en el cual se va a valuar la función; por ejemplo, los
términos s0 zi , s0 z2 y s0 p1 que se muestran en la figura 4.21.
Con referencia a ésta, se valúa a F(s) en el contorno C, recorriéndolo en la dirección
indicada, después de una revolución completa, los vectores que van desde los ceros
y los polos que no se encuentran rodeados por el contorno, mantienen constante su
contribución en fase al lugar de la función. No pasa lo mismo con el vector que se
origina en el cero z2 , que por estar rodeado por el contorno, incrementa su fase en
360°. Es por esto que la gráfica rodea el origen del plano F, en la misma dirección que
el contorno C en s, sobre el cual se ha valuado la función. Si en lugar de haberse
rodeado un cero, se tuviera un polo, es evidente que el vector originado en este,
contribuiría también con 360°, pero negativos, a la gráfica de la función, lo cual
significa que el lugar F(s) rodea el origen, pero en sentido contrario de la dirección
del contorno C. Si un polo y un cero fueran rodeados por el contorno, las
contribuciones en fase de ambos se anulan y el lugar de F(s) no encircularía el
origen. Como se puede notar, el número de encirculamientos en torno al origen en el
plano F, viene dado por la diferencia del número de ceros (Z) y de polos (P) que son
rodeados por el contorno en s.
Esto es:
N=Z-P
Si la diferencia es positiva, el origen del plano F(s) será rodea do en la misma
dirección que el contorno en el plano s y si la diferencia es negativa, el rodeo del
origen en F será en sentido contrario, esto, independientemente del sentido que se
haya dado al contorno en s, ya sea el de las manecillas del reloj o contrario. Cuando
el rodeo en el plano F es en el mismo sentido que el del contorno en s, se dice que
el origen y la región rodeada por el lugar de F(s) está incluida y si el rodeo es en
sentido contrario, excluida.
CRITERIO DE NYQUIST.
Considérese el sistema de control retroalintentado que se muestra en la figura
siguiente
Cuya función de transferencia en cadena cerrada está dada por:
C ( s)
R( s )
G( s)
1 G( s) H ( s)
La estabilidad de este sistema, se asegura cuando las raíces de su ecuación
característica, están localizadas en la región real negativa del plano complejo. Es
decir, que las raíces de 1+G(s) H(s)= 0 sean reales negativas o complejas con
parte real negativa. El término 1+G(s)H(s) que se representará con F(s), se conoce
como función característica y con frecuencia viene dado por una razón de
polinomios, tal que:
F ( s) 1 G( s) H ( s)
En donde - z1 , z2 ,......, zm y
( s z1 )( s z2 ).....( s zm )
( s p1 )( s p2 ).....( s pn )
(n
m)
p1 , p2 ,......, pn son respectiva mente los ceros y los
polos de la función. Ahora bien, si se hace F(s)=0 para encontrar las raíces de
la ecuación característica, se tiene que:
F ( s) 1 G( s) H ( s)
( s z1 )( s z2 ).....( s zm )
De donde resulta que los ceros de F(s) son las raíces de la ecuación
característica, o lo que es lo mismo, los polos de la función de transferencia en
cadena cerrada C(s)/R(s) . Por otro lado, si se despeja a G(s)H(s) del valor de F(s),
se tiene:
G( s) H ( s)
F ( s) 1
( s z1 )(s z2 ).....(s zm ) (s p1 )(s p2 ).....(s
( s p1 )( s p2 ).....( s pn )
pn )
Como se observa los polos de la función de transferencia en cadena abierta
G(s)H(s) son los polos de la función característica F(s)= 1 + G(s)H(s) . Estos
últimos conceptos son muy importantes para la discusión del criterio de
estabilidad que se verá a continuación.
Supóngase se traza un contorno en el plano "s", como el mostrado en la fig. 4.24,
el cual rodea completamente la región real positiva del plano complejo. Este
contorno que no debe pasar por ninguna singularidad (polo) de F(s), recibe el
nombre de camino de Nyquist y si se valúa a F(s) = 1+G(s)H(s) a lo largo de el, el
lugar de la función rodeará el origen del plano F, tantas veces como la diferencia
de ceros y polos que se hallen en el semiplano positivo, esto es:
N=Z-P Si N > 0, el origen del plano F será rodeado N veces en el mismo sentido,
que el camino de Nyquist en el plano "s", siendo el sistema inestable. Recuérdese
que para tener un sistema estable, no debe haber ni un sólo cero de F(s) en el
semiplano positivo del plano complejo.
Si N < 0, el origen del plano F será rodeado N veces, pero ahora en sentido
contrario al del camino de Nyquist. Como N indica solo la diferencia entre ceros y
polos, para asegurar la estabilidad del sistema, el numero de rodeos N debe ser
exactamente igual al número de polos, esto es Z=0.
Si N = 0, el origen del plano F no será rodeado por el lugar de F(s). En este caso
para que el sistema sea estable, tanto Z como p deben ser iguales a cero.
Como la función de transferencia en cadena abierta G(s)H(s), es más fácil de
trazar que F(s) y siendo sus lugares idénticos, salvo una translación del eje
complejo, el criterio de estabilidad se define generalmente con respecto a la
gráfica G(s)H(s). Ya que G(s)H(s) = F(s) - 1, el origen del plano F corresponde
al punto (-1, j0) del plano GH, de tal manera que los rodeos en el plano GH no se
referirán a su origen, sino al punto mencionado. Por otro lado, siendo los polos de
G(s)H(s) iguales a los de F(s), el camino de Nyquist trazado en el plano s para la
función característica, se puede aplicar a la función en cadena abierta. En la
mayoría de los casos, las funciones de transferencia en cadena abierta de los
sistemas físicos, son funciones estables, ya que carecen de polos en el
semiplano s positivo. De esta manera, si P=0, el número de rodeos del punto (-1,
j0) por el lugar de G(s)H(s), estará determinado por el número de ceros que se
encuentren en la región, esto es N=Z. Así un sistema será estable si el punto (1, j0) no es rodeado por el lugar de G(s)H(s) . Como los rodeos del punto (-1, j0)
debidos a los ceros, si los hay, serían en la misma dirección de la del camino de
Nyquist, esto es, incluyendo la región y al punto mencionado, se acostumbra
decir que cuando el sistema es estable, el punto (-1, j0) no es incluido. En la
figura 4.26 se muestran las gráficas de ciertos lugares G(s)H(s), con los que se
puede determinar la estabilidad del sistema en cadena cerrada, del que son
parte. Para el sistema estable mostrado en la figura 4.26, el punto (-1, j0), no es
rodeado ni incluido por el lugar de G(s)H(s). En cambio, para el otro, el punto (-1,
j0) no es rodeado e incluido dos veces por el lugar de G(s)H(s), de tal manera que
si P=0, se tienen dos ceros (raíces de la ecuación característica) en la región real
positiva del plano s, de ahí su característica de inestabilidad.
CRITERIO DE NYQUIST SIMPLIFICADO.
Cuando la función de transferencia en cadena abierta, tiene sus polos situados
fuera de la región real positiva del plano s, esto es P=0 (lo cual ocurre en la
mayoría de los casos) no es necesario evaluarla sobre todo el camino de Nyquist
para determinar la estabilidad; basta simplemente trazar el lugar de G(s)H(s), para
el tramo que va desde el origen del plano s hasta s
, esto es, de
0 a
Para los sistemas de la figura anterior se tendrían las gráficas que se muestran
en la fig. 4.27.
En el caso en que la gráfica de G(s)H(s), llegara a pasar por el punto crítico (-1,
j0), se tendrá que la función característica F(s), tiene un cero localizado en el
semieje positivo imaginario del plano complejo (recuérdese que se está valuando
a la función desde
0 a
) y como los ceros de F(s) son los polos de la
función de transferencia en cadena cerrada, esta raíz compleja y su conjugado,
que debe localizarse en la porción negativa del eje imaginario, originan una
.
respuesta oscilatoria, ante cualquier señal a que se vea sometido el sistema.
Los sistemas con esta característica se conocen como marginalmente estables,
aunque prácticamente son inestables, fig.4.28
APLICACIÓN DEL CRITERIO DE NYQUIST.
A continuación se tratarán varios ejemplos que servirán para ilustrar la aplicación
del criterio de estabilidad.
Ejemplo: Se desea determinar la estabilidad del sistema retroalimentado que tiene
la siguiente función de transferencia en cadena abierta.
G( s) H ( s)
K
s(Ts 1)
Siendo K y T reales positivos.
Obsérvese que los polos de G(s)H(s) (que son los mismos de F(s)), se encuentran
fuera de la región real positiva del plano complejo, de ahí que si hay
encirculamientos del punto (-1, j0) son debidos a ceros de F(s) y por lo tanto el
sistema sería inestable. En la figura 4.29 se muestra la localización de los polos de
la función, así como el contorno de Nyquist, que para no pasar por el polo que se
halla en el origen efectúa un pequeño semicírculo.
Como P = 0, para determinar la estabilidad del sistema, bastaría con evaluar a la
función en el tramo del camino de Nyquist, que va desde
0 a
embargo, se hará en toda su extensión, para ilustrar su aplicación.
sin
Ya sea que se considere todo el camino o solamente una parte de él, sería
deseable tomar un gran numero de valores de s, para -tener una gráfica mas
exacta de la función, sin embargo, el trazado asintótico suele ser en muchas
ocasiones suficiente. Valuando inicialmente a la función a lo largo del eje imaginario,
desde s
j0 ó
0 hasta s
ó
j
G( s ) H ( s )
, se tiene:
0
G( s ) H ( s )
El lugar de G(s)H(s), para el tramo que va desde s
90º
0 180º
j
ó
hasta s
j0 ó
0 , es simétrico al lugar anterior. En la fig. 4.30 se puede observar el trazo de
los tramos mencionados.
Para evaluar a la función en el pequeño rodeo alrededor del origen, los puntos que
constituyen el camino se representan por un vector giratorio.
s
Cuyo módulo ρ es muy pequeño (
ej
0 ) y su ángulo de fase varía de -90° a +90°,
de tal modo que el vector se desplaza 180°, en sentido contrario de las
manecillas del reloj. Así:
G( s) H ( s) s
Al tender
K
ej
K
j
e (T e
j
1)
T
2 2j
e
ej
0 la expresión anterior puede simplificarse. Esto es:
K
G( s) H ( s) s e j
ej
j
e
De esta manera el lugar de la función está dado por un semicírculo, cuyo módulo
tiende a ∞ y su ángulo de fase va de +90 a -90°; esto ultimo, porque en el término
anterior el ángulo θ que variaba de -90° a +90°, tiene signo negativo. En la figura
4.31 se puede observar el tramo del camino de Nyquist y su lugar
correspondiente en el plano de la función.
El último tramo del camino de Nyquist en el que falta evaluar a G(s)H(s), es el lugar
de s que con radio tendiendo a ∞ , se mueve de +j∞ a -j∞. De manera similar al
caso anterior, los puntos que forman este tramo se representan por un vector
giratorio:
ej
s
Con modulo ρ ∞ y el ángulo θ variando de +90° a -90°. De esta menera:
G( s) H ( s) s
K
ej
T
2 2j
e
e
j
K
T 2 e2 j
0e2 j
En la figura 4.32 se puede observar el lugar de la función, que viene dado por un
vector, cuyo módulo tiende a cero en tanto gira 360° en sentido contrario al de las
manecillas del reloj.
A continuación se muestra el lugar de Nyquist completo y como se puede observar el
lugar de G(s)H(s) no rodea (ni incluye) al punto (-1, j0) por lo tanto el sistema en
cadena cerrada es estable. Ejemplo: Se desea determinar la estabilidad del siguiente
sistema:
G( s) H ( s)
K
s(T1s 1)(T2 s 1)
Para el tramo que va desde –j0 a +j0 se considera el vector giratorio
ej
s
En donde ρ es muy pequeño ( ρ0) y se desplaza 180°, desde --90° a + 90°. De
esta manera:
G( s) H ( s) s
ej
j
e (T1 e
j
K
1)(T2 e j
1)
j
e [TT
1 2
2 2j
e
K
(T1 T2 ) e j
1]
Como ρ0 la expresión anterior se puede simplificar
G( s) H ( s) s
ej
K
ej
ej
El tramo del camino de Nyquist y su lugar correspondiente, se puede observar en la
figura 4.36. Nótese que en tanto el lugar en el plano s se mueve en el sentido contrario
a las manecillas del reloj, el lugar de G(s)H(s) lo hace en el mismo sentido.
Para el último tramo del camino de Nyquist, en donde s va de + j∞ a -j∞ se considera
el vector giratorio
s
ej
En donde ρ∞ y el ángulo de fase va de +90 a -90 o.De esta mane ra:
G( s) H (s) s
ej
j
e (T1 e
j
K
1)(T2 e j
1)
Como ρ∞, entonces:
G( s) H ( s) s
K
ej
TT
1 2
3
e
j3
0e j 3
En la fig. 4.37 se muestra el lugar de la función, que viene dado por un vector con
módulo tendiente a cero, en tanto gira 540° en sentido contrario a las
manecillas del reloj.
En la figura 4.38 se muestra el lugar completo de G(s)H(s). Obsérvese que el
sistema puede ser o no estable, dependiendo del valor -del modulo de la función,
cuando corta al eje real negativo. Es evidente que esto depende de los valores
que tomen los parámetros del sistema K, T1 y T2. Por lo general T1 y T2 son
magnitudes que no se pueden variar, así que la estabilidad del sistema está en
función del valor que tome la ganancia K.
Por ejemplo, supóngase que T1 y T2 son respectivamente 1 y 0.5, en tanto que K
toma el valor de 5, esto es:
G( s ) H ( S )
G( s ) H ( S )
5
s(s 1)(0.5s 1)
5
s(s 1)(0.5s 1)
Como el lugar de G(s)H(s) corta al eje real, cuando es evaluado sobre el eje
imaginario del plano s, se sustituye la variable s por jω. De esta manera.
G(s) H (S )
5
1)(0.5 j
j (j
2, 25
2
5
1)
7,5
(1 0,5
1,5
2
5
2
j (1 0,5
)
1,5
2
j (1 0,5
2
)
.
1,5
1,5
2
2
j (1 0,5
j (1 0,5
2
2 2
)
j
5(1 0,5 )
2, 25 2
(1 0,5
2 2
)
Cuando la gráfica de la función corta al eje real, su parte imaginaria se anula, tal que:
5(1 0,5 2 )
2, 25 2
(1 0,5
2 2
)
0
de donde:
2
Este valor de frecuencia, es al cual ocurre del eje real. Sustituyendo w=V2 en la
ecuación de la función, se obtiene la intersección:
G( j 2) H ( j 2)
7,5
2, 25.2 (1 0,5.2)2
1,66
2
2
)
)
Aplicando el criterio simplificado, en la figura mostrada a continuación, se puede
observar como la gráfica de G(s)H(s) incluye el punto crítico (-1, j0), de donde el
sistema para este valor de ganancia (K = 5) es inestable
Continuando con el ejemplo, supóngase ahora que el valor de K se reduce a 2, es
decir:
G( s ) H ( S )
2
s(s 1)(0.5s 1)
Sustituyendo s por jω:
G( s) H ( S )
j (j
2
1)(0.5 j
1)
2, 25
2
3
(1 0,5
2 2
)
j
2(1 0,5 2 )
2, 25 2
(1 0,5
2 2
)
Haciendo la parte imaginaria igual a cero, se encuentra que la frecuencia a la
cual la función, corta el eje real, tiene el mismo va lor que en el caso anterior, es
decir
2 . De esta manera la intersección con el eje real viene dada por:
G( j 2) H ( j 2)
3
2, 25.2 (1 0,5.2)2
0,66
En la figura 4.40 se muestra la gráfica de la función, en donde se puede observar que
el punto crítico no es incluido por ésta, por -lo tanto el sistema es estable.
Del ejemplo se desprende, que entre menor sea el valor de la ganancia, el sistema
es más estable. El valor crítico de K, esto es, el máximo que puede tomar sin hacer
inestable al sistema se puede obtener aplicando el criterio de Routh. Siendo la
ecuación característica del sistema:
0,5s 3 1,5s 2
El arreglo de Routh es el siguiente:
s3
0,5
2
1,5
s
s1
1,5 0,5 K
1,5
s0
K
s K
0
Las condiciones de estabilidad son:
1,5 0,5 K
1,5
K
0
0
De donde
K
3
Esto significa que el sistema se comportará estable si la ganancia toma valores
menores que 3. Si K=3 se tiene el caso de estabilidad marginal. Por último para
valores de K > 3 el sistema es inestable.
4.7.- ESTABILIDAD RELATIVA.
Se ha mencionado que la utilidad de un sistema de control, depende del grado de
estabilidad que tenga. Esto es, no basta que sea estable, sino que debe serlo en
cierta medida. Para determinar el grado o medida de estabilidad de un sistema, se
pueden aplicar los métodos de respuesta frecuencial.
En la figura 4.41 se muestran las gráficas de respuesta de un sistema para
diferentes valores de ganancia. Obsérvese que si -esta es elevada, el lugar de la
función se acerca peligrosamente al pinito crítico (-1, j0), en tanto que al reducirse se
aleja de él. Evidentemente en el primero de los casos (K elevado) la estabilidad
del sistema será menor.
En general, cuanto más se acerque la gráfica de G(jω)H(jω) al punto crítico, el sistema
se hace más oscilatorio en su respuesta. De esta manera, se puede emplear la
distancia entre el lugar de la función y el punto (-1, j0) como una medida de la
estabilidad relativa del sistema. Esta distancia se expresa en términos del margen
de fase y de ganancia.
MARGEN DE GANANCIA.
El margen de ganancia se define como el recíproco de |G(jω)H(jω)| cuando el ángulo
de fase es de -180°. Denotándose con
f
, la frecuencia a la cual ocurre el corte
del eje real negativo, se tiene:
MG
1
G( j f ) H ( j
f
)
Que expresado en decibeles queda como:
MG, dB
20log
1
G( j f ) H ( j
f
)
Cuando |G(jω)H(jω)| < 1, el margen de ganancia es positivo y se puede interpretar como la
ganancia mínima adicional, que hace inestable al sistema. En caso contrario cuando
|G(jω)H(jω)| > 1, el margen de ganancia es negativo y se interpreta como la ganancia
mínima, que debe reducirse para llevar al sistema al margen de la estabilidad. En la
figura 4.42 se puede ver el margen de ganancia, nótese que para un sistema
estable, corresponde un margen de ganancia positivo.
MARGEN DE FASE.
El margen de fase se define, como el ángulo que hay entre el eje real negativo y el
lugar de la función cuando su modulo es unitario. La frecuencia a la cual ocurre, se
denota por
g
. El margen de fase se designa por
siendo
180º
en donde
es negativo. En la figura 4.43 se puede observar el margen de fase tanto para
un sistema estable como para uno inestable. Para el primero corresponde un
margen de fase positivo (
(
0)
0 )y para el segundo un margen de fase negativo
MARGENES DE GANANCIA Y DE FASE EN LOS LUGARES DE BODE Y
BLACK.
El margen de ganancia y el margen de fase, se pueden definir en -las gráficas
logarítmicas de Bode y de Black, lo cual resulta muy conveniente por la sencillez de
su trazo. En la figura 4.44 se pueden observar estas cantidades representadas
gráficamente.
Para determinar la estabilidad de los sistemas, es conveniente establecer tanto el
margen de fase, como el de ganancia, los cuales deben ser positivos en sistemas
estables y de valor comprendido entre los 30° y 60° el primero y no menor de 6 dB el
segundo, para asegurar un comportamiento satisfactorio.