Criterio de Nyquist

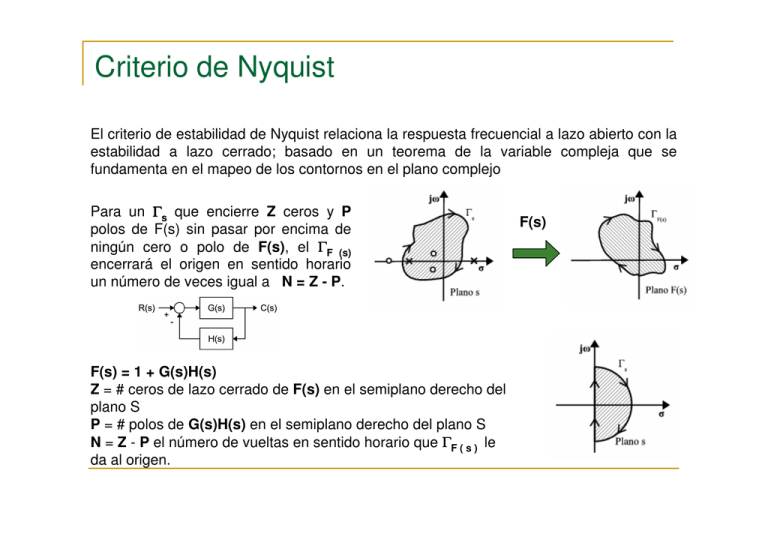
Criterio de Nyquist
El criterio de estabilidad de Nyquist relaciona la respuesta frecuencial a lazo abierto con la
estabilidad a lazo cerrado; basado en un teorema de la variable compleja que se
fundamenta en el mapeo de los contornos en el plano complejo
Para un Γs que encierre Z ceros y P
polos de F(s) sin pasar por encima de
ningún cero o polo de F(s), el ΓF (s)
encerrará el origen en sentido horario
un número de veces igual a N = Z - P.
F(s) = 1 + G(s)H(s)
Z = # ceros de lazo cerrado de F(s) en el semiplano derecho del
plano S
P = # polos de G(s)H(s) en el semiplano derecho del plano S
N = Z - P el número de vueltas en sentido horario que ΓF ( s ) le
da al origen.
•
•
•
F(s)
Criterio de Nyquist
Para que el sistema sea estable
Z debe ser cero
Si P = 0 entonces N = 0
Si P ≠ 0 entonces N = - P
F’(s) = F(s) – 1 = G(s)H(s)
P’ y Z’ son los polos y ceros de lazo abierto
P’= P (polos de lazo cerrado = Polos de lazo abierto)
N’ corresponde al número de encierros que le da el ΓF’(s) al punto (-1,0) (N’ = N)
La transformación sobre el Plano F’(s), se realiza tomando en cuenta que el Γs no
debe pasar por ningún polo o cero de F’(s)
El ΓF’(s) se conoce como el Diagrama de Nyquist.
Los ceros de la Ecuación característica a lazo cerrado (Z) se puede conocer a
partir de N’ y de P, pues N’ = Z – P’
Para que el sistema sea estable
Z debe ser cero
Si P = 0 entonces N’ = 0
Si P ≠ 0 entonces N’ = - P
Criterio de Nyquist
Ejemplos
Tramo I
(Diagrama Polar)
Tramo II
Tramo III
(simétrico al Diagrama Polar)
Criterio de Nyquist
Ejemplos
Conclusión
Como P = 0 (el Γs no encierra ningún polo de G(s)H(s)) y N = 0 (el Diagrama de Nyquist
no encierra el punto (-1,0)), entonces Z = 0 siendo el sistema estable.
Además, también se puede concluir que será estable para cualquier ganancia pues nunca
se encerrará al punto (-1,0)
Criterio de Nyquist
Ejemplos
Tramo I
(Diagrama Polar)
Tramo II
Tramo III
(simétrico al Diagrama Polar)
Criterio de Nyquist
Ejemplos
Tramo IV
Conclusión
Si la ganancia es tal que el Diagrama de Nyquist queda como el que se muestra, entonces
como P = 0 (el Γs no encierra ningún polo de G(s)H(s)) y N = 0 (el Diagrama de Nyquist no
encierra el punto (-1,0)), entonces Z = 0 siendo el sistema estable. Si por el contrario, la
ganancia fuese mayor y el punto (-1,0) quedara dentro del diagrama, entonces N = 1 por
lo que el sistema sería inestable a lazo cerrado. Por lo tanto la estabilidad depende del
valor de la ganancia.