Tema 3. Celosías hiperestáticas

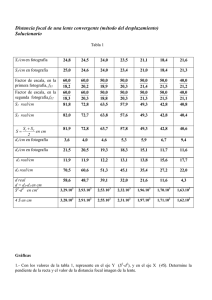
Capítulo 3
Celosías planas hiperestáticas
3.1.
Contenido
Celosías hiperestáticas. Tipos de hiperestatismos: Sustentación y constitución.
Solución mediante PTV al hiperestatismo de sustentación. Solución mediante PTV
al hiperestatismo de constitución. Tensiones térmicas. Tensiones de montaje debidas a errores en los elementos. Tensiones debidas a asientos en los apoyos.
3.2.
Objetivos
Saber identificar el grado de hiperestaticidad de una celosía y su origen
Saber aplicar el PTV a la resolución de celosías hiperestaticas
3.3.
Qué se debe saber al terminar este tema
1. Que si se comprendió bien el tema anterior éste no debe plantear ninguna
dificultad. Si lo hace significa que no se entendió bien el otro tema, repasémoslo.
2. Identificar los hiperestatismos internos y externos. Elegir una celosía primaria.
3. Que aplicar el PTV con fuerzas virtuales es equivalente a escribir ecuaciones
de compatibilidad.
4. Aplicar el PTV al calculo de esfuerzos en celosías hiperestáticas.
5. Aplicar el PTV al calculo de desplazamientos en celosías hiperestáticas.
11
CAPÍTULO 3. CELOSÍAS PLANAS HIPERESTÁTICAS
30º
AB 1 cm larga
CB 0.5 cm larga
DB +30ºC
EB –30ºC
10 kN
A
12
C
5m
B
D
Area 10 cm 2
E= 2.1e11 N/m 2
I=1420 cm 4
α=0.000012 ºC -1
E
10 m
3.4.
Ejercicios resueltos
1. Cálcular los esfuerzos en las barras de la celosía
La celosía tiene 4 incognitas (los esfuerzos en las barras ya que conocidas estas
se conocen las reacciones) y ponemos plantear 2 ecuaciones de equilibrio en el
nudo B, por lo tanto se trata de una celosía hiperestática grado 2. Sustituimos
las barras BC y BE por sus esfuerzos:
30º 10 kN
A
C
X1
X1
B
X2
X2
D
E
y se resuelve por superposición de tres estados de carga
30º 10 kN
A
A
B
X1
A
B
B
X2
D
D
D
que como puede verse se resuelve mediante el equilibrio en el nudo B. Los
esfuerzos en las barras debidos al primer caso son
Los dos sistemas siguientes se resuelven con cargas unitarias, ya que posteriormente emplearemos ese sistema como sistema virtual de fuerzas para
obtener dos ecuaciones de compatibilidad adicionales. Así,
CAPÍTULO 3. CELOSÍAS PLANAS HIPERESTÁTICAS
13
30º 10000 N
-3660
A
B
12247
N
D
A
1
A
1N
1.4142
B
B
1N
0
-1
Nv1
Nv2
D
D
Planteando el PTV, con cargas unitarias, para sobre estos últimos sistemas
se tiene que
δBC =
X
N1v
δBE =
X
N2v
l
(N + X1 N1v + X2 N2v ) + ∆l + αl∆T
AE
l
(N + X1 N1v + X2 N2v ) + ∆l + αl∆T
AE
(3.1)
(3.2)
que serán positivos cuando los puntos BC y BE se acerquen. Por otro lado,
observando las barras BC y BE, se tiene que,
δbarraBC =
δbarraBE =
lX1
+ ∆l + αl∆T
AE
lX2
+ ∆l + αl∆T
AE
(3.3)
BC
(3.4)
BE
CAPÍTULO 3. CELOSÍAS PLANAS HIPERESTÁTICAS
14
que serán positivos cuando las puntos BC y BE se alejen. Por lo tanto el
sistema de ecuaciones a resolver es
X
lX1
l
−
+ ∆l + αl∆T
(N + X1 N1v + X2 N2v ) + ∆l + αl∆T
=
N1v
AE
AE
BC
(3.5)
X
lX2
l
v
v
v
+ ∆l + αl∆T
(N + X1 N1 + X2 N2 ) + ∆l + αl∆T
−
=
N2
AE
AE
BE
(3.6)
Las operaciones a realizar aparecen en el siguiente sumatorio
Barra
f
N
Nv1
Δl
Nv2
AB
2.381·10
-8
-3660
1
1.4142
DB
3.367·10-8
12247
0
-1
αlΔt
-2
10
0
f·N·Nv1
f·N v1·Nv2
0 -8.714·10
2.545·10-3
SUMATORIOS -8.714·10
-5
3.367·10
-8
f·N·Nv2
f (Nv1)2
-1.232·10
-4
f (Nv1)2
2.381·10
-8
4.762·10-8
0
0 -4.123·10-4
0
3.367·10-8
-5
-8
-8
8.129·10-8
3.367·10
-5.35·10
-4
2.381·10
Donde f es la flexibilidad. Por lo tanto el sistema de ecuaciones que permite
obtener la solución es
4,762 · 10−8 X1 + 3,367 · 10−8 X2 = −0,01491
(3.7)
3,367 · 10−8 X1 + 1,1496 · 10−8 X2 = −8,517 · 10−3
(3.8)
De donde se obtienen -238.8 y 22.2 kN respectivamente.
N real
65.86783
158.45841
-64.34344
131.73566
-147.2849
-143.944
466.67766
-279.5694
40
-188.7046
292.17592
-96.73259
-44.72136
-457.4092
L (cm)
100
223.6068
200
200
223.6068
200
223.6068
100
200
100
223.6068
500
223.6068
200
A
B
H
200
149.1576 -116.828 143.21415
-116.8281 461.1519 -121.3315
143.2142 -121.331 507.15344
C
=
G
200
-96.73 =X1
466.68 =X2
-147.3 =X3
X1
X2
X3
f=L/AE
N
NV1 NV2
3.353E-04
0
0
0
7.499E-04 89.44 -2.236
0
6.707E-04
-80
1.2
0
6.707E-04
0
0
0
7.499E-04
0
0
0
6.707E-04
80
-2 -0.8944
7.499E-04
0
0
1
3.353E-04
-40
1 -0.4472
6.707E-04
40
0
0
3.353E-04
20
0 -0.4472
7.499E-04 -44.7 1.3416
1
1.677E-03
0
1
0
7.499E-04 -44.7
0
0
6.707E-04
-40
0 -0.8944
0.01076 0.002056 -0.002547
0.002056 0.002707 6.707E-05
-0.002547 6.71E-05 0.002707
BARRA
AB
AC
AG
BC
BG
CD
CF
CG
DE
DF
DG
DH
EF
FG
300
100
1
2
3
4
5
6
7
8
9
10
11
12
13
14
F
D
200
0.2937 =
1.0545 =
-0.121 =
E
20 kN
∆T= +30
∆EF= + 1 cm
∆CF= - 1 cm
IPN 120
-3.801E-01 8.640E-02 0.000E+00
-5.453E-02 0.000E+00 ########
1.211E-01 2.776E-17 0.000E+00
A
B
H
X3
X3
X1
X1= -96.7326
X2= 466.6777
X3= -147.285
∆T ∆L
NV3
f*N*NV1
f*N*NV2
f*N*NV3 f*NV1^2 f*NV2^2 f*NV3^2
-0.447 30 0
0
0
0
0
0 6.707E-05
1 30 0 -1.500E-01
0 6.707E-02 3.749E-03
0 7.499E-04
-0.894 30 0 -6.439E-02
0 4.799E-02 9.658E-04
0 5.366E-04
-0.894 30 0
0
0
0
0
0 5.366E-04
1 30 0
0
0
0
0
0 7.499E-04
0 30 0 -1.073E-01 -4.799E-02
0 2.683E-03 5.366E-04
0
0 30 -1
0
0
0
0 7.499E-04
0
-0.447 30 0 -1.341E-02 5.999E-03 5.999E-03 3.353E-04 6.707E-05 6.707E-05
0 30 0
0
0
0
0
0
0
0 30 0
0 -2.999E-03
0
0 6.71E-05
0
0 30 0 -4.499E-02 -3.353E-02
0 1.350E-03 7.499E-04
0
0 30 0
0
0
0 1.677E-03
0
0
0 30 1
0
0
0
0
0
0
0 30 0
0 2.400E-02
0
0 5.366E-04
0
SUMAS
-3.801E-01 -5.453E-02 1.211E-01 1.076E-02 2.707E-03 2.707E-03
C
G
X1
X2
F
D
f*NV1*NV3 f*NV2*NV3 NV1*αl∆t
0
0
0
-1.677E-03
0
-0.18
-7.199E-04
0
0.0864
0
0
0
0
0
0
0
0
-0.144
0
0
0
-1.500E-04 6.70691E-05
0.036
0
0
0
0
0
0
0
0
0.108
0
0
0.18
0
0
0
0
0
0
-2.547E-03
6.707E-05 8.640E-02
X2
f*NV1*NV2
0
0
0
0
0
1.200E-03
0
-1.500E-04
0
0
1.006E-03
0
0
0
2.056E-03
E
NV3*αl∆t NV1*∆L NV2*∆L NV3*∆L
-1.610E-02
0
0
0
8.050E-02
0
0
0
-6.440E-02
0
0
0
-6.440E-02
0
0
0
8.050E-02
0
0
0
0
0
0
0
0
0
-1
0
-1.610E-02
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
2.776E-17
0
-1
0
20 kN
NV2*αl∆t
0
0
0
0
0
-6.440E-02
8.050E-02
-1.610E-02
0
-1.610E-02
8.050E-02
0
0
-6.440E-02
0.000E+00
CAPÍTULO 3. CELOSÍAS PLANAS HIPERESTÁTICAS
15
2. Calcular los esfuerzos en la celosía de la figura
barra
AB
AF
AG
BC
BD
BF
BG
CD
CF
CH
DE
DF
EF
FG
f
N
100
0
0
100
0
0
0
75
-125
0
75
0
-125
-200
3.622E-06 2.700E-05
5.795E-05 2.912E-05
2.912E-05 1.191E-04
1.3414E-05
1.6767E-05
1.006E-05
1.3414E-05
1.6767E-05
1.006E-05
1.6767E-05
1.006E-05
1.6767E-05
2.8652E-05
1.006E-05
1.3414E-05
1.6767E-05
1.3414E-05
H
AB
AF
AG
BC
BD
BF
BG
CD
CF
CH
DE
DF
EF
FG
barra
300
0
0
0
-0.8
1
-0.6
0
-0.6
1
0
0
-0.8
0
0
NV3
=
G
F
300
E
=
=
=
0
0
0.000379
∆t= 30
DBF=+ 2 mm
DBF=-5 mm
A –1 cm vertical
IPN 120
-0.003622
0.001073
-0.006878
0
0
0
8.58E-06
1.68E-05
3.62E-06
0
3.62E-06
1.68E-05
0
0
8.58E-06
0
0
5.79E-05
4.822E-03
-1.462E-03
-1.535E-02
F*NV1^2
F*N*NV3
F*N*NV2
0 -0.001073 -0.002512
0
0
0
0
0
0
-0.001073105
0 -0.001884
0
0
0
0
0
0
0
0
0
-0.000452716
0
0
-0.002095909
0 -0.001227
0
0
0
0
0
0
0
0
0
0
0
0
0 0.002146 -0.001256
-0.00362173 0.001073 -0.006878
F*N*NV1
100 kN
-1.87265836
0
-0.35112344
-1.40449377
0
-0.35112344
0.58520574
0
0.58520574
1
0
0
0
0.46816459
sumas
D
163 =X1
54.7 =X2
-179 =X3
X1
X2
X3
-0.8
1
-0.6
0
0
-0.6
1
0
0
0
0
0
0
-0.8
NV1 NV2
300
Nreal
392.18685
54.724704
30.158917
221.26229
163.39084
-67.87559
-50.26486
-23.03451
-66.59872
-179.4062
75
-130.7127
-125
-327.7714
A
B
C
19361.886 1136.65347 -4669.518
1136.6535 19742.5265 -5087.073
-4669.518 -5087.07259 10702.769
5.795E-05
3.622E-06
2.700E-05
4
5
3
4
5
3
5
3
5
8.5440037
3
4
5
4
l (m)
400
400
1
2
3
4
5
6
7
8
9
10
11
12
13
14
F*NV2^2
-0.0012
0.0003888
0.0031264
8.5848E-06
1.6767E-05
3.6217E-06
0
0
3.6217E-06
1.6767E-05
0
0
0
0
0
0
8.5848E-06
5.7948E-05
H
4.704E-05
0
1.2403E-06
2.646E-05
0
1.2403E-06
5.7422E-06
0
5.7422E-06
2.8652E-05
0
0
0
2.94E-06
0.00011906
F*NV3^3
0
0
0
1.5072E-05
0
2.1195E-06
0
0
9.8123E-06
0
0
0
0
0
2.7003E-05
X3
X3
A
B
C
X2
X2
X1
2.0096E-05
0
2.1195E-06
0
0
2.1195E-06
9.8123E-06
0
0
0
0
0
0
-5.024E-06
2.9123E-05
X1
Rv
As
1.87265836
-1.00E-02
0
0
0
0
0
3.6217E-06
0
0
0
0
0
0
0
0
3.6217E-06
F*NV1*NV2 F*NV1*NV3 F*NV2*NV3
D
DL
G
F
E
0
0
0
-0.00115
0.0018
-0.00065
0
-0.00065
0.0018
0
0
-0.00115
0
0
0
-0.001152
0.0018
-0.000648
0
0
-0.000648
0.0018
0
0
0
0
0
0
-0.001152
0
-0.00269663
0
-0.00037921
-0.00202247
0
-0.00037921
0.00105337
0
0.00105337
0.003075841
0
0
0
0.000674157
0.000379213
NV1*αL∆T NV2*α*L*∆T NV3*α*L*∆T
100 kN
30
0
30
0
30
0
30
0
30
0
30 2.00E-03
30
0
30
0
30
0
30
0
30 -5.00E-03
30
0
30
0
30
0
163.39 =X1
54.72 =X2
-179.41 =X3
DT
NV2*∆L
NV3*∆L
0
0 0.0021573
0
0
0
0
0 0.0002275
0
0
0
0
0
0
-0.0012 0.000389 0.0002275
0
0 0.0010534
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0 -0.000539
-0.0012 0.000389 0.0031264
NV1*∆L
CAPÍTULO 3. CELOSÍAS PLANAS HIPERESTÁTICAS
16
3. Calcular los esfuerzos en la celosía de la figura
15 kN
500
10 kN
500
1.153E-08
1.153E-08
3.968E-08
1.18447E-07 1.84E-08
1.83934E-08 1.18E-07
1.15325E-08 1.15E-08
15 kN
N1
N2
N3
Δt=±30
Acero
-52088
-78214
-1.7E-06 0.002906
-1.7E-06
0.01
-0.0036
0.005
=
=
=
46036
62089
-0.001218
= -0.002307
0.000368
-30329
-39660
=
=
=
-13976
2078
-0.001218 1.67E-06 0.002906
= -0.002307 1.67E-06
0.01
0.000368
0.0036
0.005
-6877
-16208
A=12 cm 2
-189994
-8554
0.001687
0.007691
0.001768
0.00169
0.007695
0.008968
-63461
-76524
77987
94040
+30º
-30º
N1= 2077.5409
N2= 62088.923
N3=
25917.5
N1= -13975.577
N2= 46035.805
N3= 216688.19
-243446
-62006
AF
BC
BF
CD
CE
CF
DE
DF
EF
5
5
8.6
5
8.6
7
7
8.6
5
1.984E-08 1.984E-08 3.41E-08 1.98E-08 3.41E-08 2.78E-08 2.78E-08 3.41E-08 1.984E-08
18571
-15000
0
-3571.4
0
-26000
-26000
31951
0
-0.581238 -0.5812382
1
0
0 -0.81373
0
0
0
0
0
0 -0.58124
1 -0.81373 -0.813733
1 -0.5812382
-1
0
0
0
0
0
0
0
-1
SUMAS
-0.000214
0.000173
0
0
0 0.000588
0
0
0 0.0012175
0
0
0 4.12E-05
0 0.000588 0.000588 0.00109
0
0.002307
-0.000368
0
0
0
0
0
0
0
0 -0.0003685
6.703E-09 6.703E-09 3.41E-08
0
0 1.84E-08
0
0
0 1.184E-07
0
0
0 6.7E-09 3.41E-08 1.84E-08 1.84E-08 3.41E-08 6.703E-09 1.184E-07
1.984E-08
0
0
0
0
0
0
0 1.984E-08 3.968E-08
0
0
0
0
0 1.84E-08
0
0
0 1.839E-08
1.153E-08
0
0
0
0
0
0
0
0 1.153E-08
0
0
0
0
0
0
0
0 1.153E-08 1.153E-08
0.0018
0.0018 0.003096
0.0018 0.003096 0.00252
0.00252 0.003096
0.0018
-0.001046 -0.0010462 0.003096
0
0 -0.00205
0
0
0 -1.674E-06
0
0
0 -0.00105 0.003096 -0.00205 -0.002051 0.003096 -0.0010462 -1.674E-06
-0.0018
0
0
0
0
0
0
0
-0.0018
-0.0036
-0.0018
-0.0018 -0.003096
-0.0018
-0.0031 -0.00252 -0.00252
-0.0031
-0.0018
0.0010462 0.0010462 -0.003096
0
0 0.002051
0
0
0 1.674E-06
0
0
0 0.001046
-0.0031 0.002051 0.002051
-0.0031 0.0010462 1.674E-06
0.0018
0
0
0
0
0
0
0
0.0018
0.0036
5.00E-03
-1.00E-02
0 -0.002906
0
0
0
0
0
0
0
0 -0.0029062
0
0
0
0
0
0
0
0
-0.01
0
-0.01
0
-0.005
0
0
0
0
0
0
0
0
-0.005
AC
8.6
3.413E-08
19662
1
0
0
0.000671
0
0
3.413E-08
0
0
0
0
0
0.003096
0.003096
0
0
-0.003096
-0.003096
0
0
5686
21740
0
0
0
AB
7
2.78E-08
0
-0.81373
0
0
0
0
0
1.84E-08
0
0
0
0
0
0.00252
-0.00205
0
0
-0.00252
0.002051
0
0
11372
-1691
Asiento 2 cm
700
ESFUERZOS (N)
barra
Longitud
f
N
N1
N2
N3
f*N*N1
f*N*N2
f*N*N3
f*N1^2
f*N2^2
f*N3^2
f*N1*N2
f*N1*N3
f*N2*N3
ALFA*L*dt
Alfa*l*dt*N1
Alfa*l*dt*N2
Alfa*l*dt*N3
ALFA*L*dt
Alfa*l*dt*N1
Alfa*l*dt*N2
Alfa*l*dt*N3
DL
DL*N1
DL*N2
DL*N3
CAPÍTULO 3. CELOSÍAS PLANAS HIPERESTÁTICAS
17
4. Calcular los esfuerzos en la celosía de la figura
Nv
Ncompatible
f*Nv*Nc
Nv*α*l*Dt
Nv*Dl
9.5319E-05
3.77423E-06
9.51736E-05
X1= -48.44824451
X2=
-20.3861404
X3= 39.58480841
7.34286E-06
9.51736E-05
3.77423E-06
-13.92418081 -54.58165263
X1
X2
X3
-20.34659152
39.5848084
10.47847617 -20.3861404
E=2.1e11
α=1.2e-5
DT=+30C
Errores de montaje:
CF +1 mm
AB –0.5 mm
Asiento en G 2 mm hacia abajo
f*N*Nv
DT*Nv
DL*Nv
-0.00175873
0
0
-0.00114372 -2.84536E-06
-0.001
-0.00049621 -2.84536E-06 -0.0004285
A
B
C
3 00
12 -2.529077678
G
F
D
300
-23.32
20 kN
E
6.82289337
f*Nv*Nc
1.29E-04
Nv*α*l*Dt
-3.60E-03
Nv*Dl
-5.00E-04
Asiento
0.004
AF
AG
BC
BD
BF
BG
CD
CF
DE
DF
EF
FG
1
0
0
0
1.166
-0.6
0
0
0
0.6
-1
-1.166
-2
-13.92418081 -54.58165263 -20.34659152 17.47092232 2.933859601 26.58012915 39.5848084 10.47847617 -20.3861404
12 -2.529077678
-23.32 6.82289337
-0.000331528
0
0
0 9.49857E-05
-0.00022783
0
0
0 0.00010286 6.02161E-05
0.000755 -0.0003249
0.0018
0
0
0
0.0024476
-0.000648
0
0
0
0.000648
-0.0018 -0.0024476
-0.0036
-5.00E-04
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
AB
Desp= 2.88E-05
1.29E-04
-3.60E-03
-5.00E-04
SUMAS
=
=
=
26.58012915
REACCIO
-0.00509206 -0.003333333
-0.00214657
0
-0.00092755
0
17.47092232 2.933859601
AF
AG
BC
BD
BF
BG
CD
CF
DE
DF
EF
FG
5.830951895
3
5 5.830951895
3 5.83095189
3 5.83095189
3
5 5.83095189
5
2.77664E-05 1.42857E-05 2.38095E-05 2.77664E-05 1.42857E-05 2.7766E-05
1.42857E-05 2.7766E-05 1.4286E-05 2.38095E-05 2.7766E-05
2.381E-05
30
30
30
30
30
30
30
30
30
30
30
30
1.00E-03
0
0
0
23.32
-12
0
0
0
12
-20
-23.32
-40
1.943650632
0
0
0
-1
0
0
0
0
0
0 -1.66666667
-0.857
1
-0.514
-0.514
1
-0.857
1
-0.514
-0.514
1
-0.857
0
0
0
0 0.000171429
0
0
0
0
0
0
0.0015873
0
0
0 0.000647513 8.81143E-05
0
0
0
0 0.000408095
0
0
0
0
0
0 8.81143E-05
0
0
0
0
0
0 0.00081619
8.99471E-05
0
0
0 2.38095E-05
0
0
0
0
0
0 6.6138E-05
0
0 1.74869E-05 2.38095E-05 6.29038E-06
0
6.29038E-06
2.381E-05
0 1.74869E-05
0
0
2.38095E-05 6.29038E-06
0
0 6.29038E-06
2.381E-05
0
0
0
0
0 1.7487E-05
0
0
0
0 7.34286E-06
0
0
0
0
0
0
0
5.39683E-05
0
0
0 7.34286E-06
0
0
0
0
0
0 3.4008E-05
0
0
0
0 3.77423E-06
0
0
0
0
0
0
0
0.00408
0
0
0
-0.00108
0
0
0
0
0
0
-0.003
0
0
-0.0015426 0.002099143
-0.00055512
0
-0.00055512 0.00209914
0
-0.0015426
0
0
0.002099143
-0.00055512
0
0 -0.00055512 0.00209914
0
0
0
0
0 -0.0015426
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
1.00E-03
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
0.00E+00
Isostaticos eliminando el apoyo B, y las barras CF y BG
0.000179894
7.34286E-06
9.5319E-05
5
2.38095E-05
30
-5.00E-04
20
0
-0.857
0
0
-0.000408095
0
0
1.74869E-05
0
0
0
0
0
-0.0015426
0.00E+00
0.00E+00
4.29E-04
AB
Desplazamiento vertical del punto E
ESFUERZOS
0.00175873
0.001143723
0.00049621
0.000179894
9.51736E-05
9.51736E-05
7.34286E-06
9.5319E-05
3.77423E-06
0
2.84536E-06
2.84536E-06
0
0.001
0.0004285
SUMAS
500
500
L
f
dt
DL
N
N1
N2
N3
f*N*N1
f*N*N2
f*N*N3
f*N1^2
f*N2^2
f*N3^2
f*N1*N2
f*N1*N3
f*N2*N3
N1*α*l*DT
N2*α*l*DT
N3*α*l*DT
N1*DL
N2*DL
N3*DL
CAPÍTULO 3. CELOSÍAS PLANAS HIPERESTÁTICAS
18
5. Calcular el desplazamientos vertical en el punto de aplicación de la carga
CAPÍTULO 3. CELOSÍAS PLANAS HIPERESTÁTICAS
3.5.
19
Ejercicios propuestos
1. En la estructura, las barras horizontales y verticales tienen un área de 6.45
cm2 , y las barras diagonales 9.12 cm2 . Material de las barras E = 0.7 106
N/mm2 y α = 18∆10−6 C −1 . Se pide:
Esfuerzos en todas las barras bajo la carga de 45.4 kN indicada
Desplazamiento vertical del nudo E en el caso anterior
Desplazamiento vertical del nudo E si además de la carga indicada,
todas las barras están sometidas a un incremento de temperatura de
27.8 C y la barra DE es 0.25 cm más larga que su longitud teórica
2.54 m
2.54 m
2.54 m
45.4 kN
D
E
2.54 m
-8.192
+17.75
-9.558
-1.931
-38.62
+1.365
+25.585
-18.092
-1.931
+1.365
-18.092
Dy = 0.4071 cm hacia abajo y 0.1939 cm hacia abajo
2. En la celosía de la figura, calcular los esfuerzos en todas las barras y reacciones en los apoyos, debido a la actuación simultánea de todas las acciones
indicadas (cargas exteriores y asientos de apoyos). Datos: área de todas las
barras 20 cm2 ; E = 2,1∆105 N/mm2 . Barra AC 1 mm más corta
CAPÍTULO 3. CELOSÍAS PLANAS HIPERESTÁTICAS
200 kN
400 kN
20
300 kN
100 kN
5m
A
C
2 x 5m = 10 m
0,5 cm
1 cm
1 cm
Asientos de apoyos
1,2 cm
1 cm
Solución
-33.02
66.98
-133.02
504
-94.73
-400
504
46.69
-333.02
0
404
133.02
433.97
333.02
3. Un procedimiento para resolver la hiperestaticidad de la estructura representada consiste en suprimir dos de sus barras e imponer ciertas condiciones
de deformación. Las dos barras a suprimir no pueden ser elegidas arbitrariamente, sino que la estructura resultante debe cumplir ciertas condiciones.
Analizar las cuatro posibilidades a), b), c) y d) presentadas, y responder de
forma razonada cual/es es/son adecuada/s para desarrollar el procedimiento
descrito
a
b
c
d
CAPÍTULO 3. CELOSÍAS PLANAS HIPERESTÁTICAS
21
4. En la celosía de la figura todas las barras tienen la misma sección y módulo
de elasticidad. Calcular sus esfuerzos. E = 2,1∆1011 N/m2 y A =14.7 cm2 .
G
F
B
C
D
6m
H
A
E
40000 kg
4x4.5m
-21857
H
-10443.8
G
11428
-3067.7
30857
-37500
F
-7593.5
6074.8
-12500
-1071.7
4906.4
A
1218.9
B
8075.8
C
-2368.1
-6924.2
D
E
5. Cálcular los esfuerzos en la celosía de la figura que está formada por barras
de acero con una sección de 16 cm2 . Calcular el desplazamiento de algún
nudo
700
300
600
B
500
C
20000 N
A
30000 N
63.9
Ux
Uy
A
3.24·10-4
-2.86·10-3
B
-6.24·10-4
-2.22·10-3
C
-4
-5.46·10-3
33.87
-30.5
-20.22
-19.6
0
-1.23·10
42.9
-15.54
Esfuerzos en kN
CAPÍTULO 3. CELOSÍAS PLANAS HIPERESTÁTICAS
22
6. Determinar los esfuerzos en la celosía de la figura
15kN
15kN
Cuadrado de lado L
-10.6
-10.6
4.39
0
4.39
kN
7. Hallar los esfuerzos en todas las barras. Éstas son del mismo material y
sección constante, (E = 2,1∆1011 N/m2 y A=14.7 cm2 )
100 kN
100 kN
F
-20896
E
-100000
1267
100000
D
-896
C
-61793
-55301
-99104
A
39104
B
20 kN
E
5m
F
40 kN
C
5m
D
A
B
5m
Valores en
N
8. En la celosía de la figura determinar los esfuerzos en las barras DF y DC , y los
desplazamientos de los nudos debidos a: las cargas exteriores, un incremento
de temperatura de 30 grados en la barras DF y ED y un asiento horizontal
en el apoyo C de 0.5 cm α = 1,2∆10−5 C −1 .
6m
A
B
A
B
-16442
6m
-38802
F
F
10kN
E
C
E
C
33212
-49412
33212
Dx=5.2 mm
Dy=-0.78 mm
6
2
E=2.1·10 kg/cm
2
A=17.4 cm
D
Fx=0.459 mm
Esfuerzos en N
Fy=0.567 mm
10kN
D
CAPÍTULO 3. CELOSÍAS PLANAS HIPERESTÁTICAS
23
9. Calcular el esfuerzo en la barra marcada debido a las siguientes cargas: Cargas
exteriores; Error de longitud en la barra solicitada -0.127 cm; Incremento de
temperatura de 33.3◦ C en todas las barras. Datos: Material acero. Sección
de las barras 6.45 cm2 y α = 11,6 · 10−6 C −1
600 cm
B
C
12000 kg
A
610 cm
300 cm
Solucion: 910 kg.
Desplazamiento en el punto de aplicación dela carga: ux= 4.4 mm uy= -22.4mm