X0,1. - FCEA - Facultad de Ciencias Económicas y de Administración
Anuncio

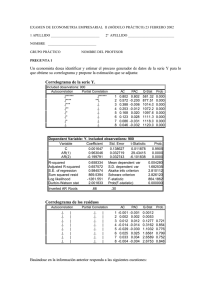
Universidad de la República, Facultad de Ciencias Económicas y Administración. ECONOMETRIA II- CURSO 2003 MODELOS DE VARIABLE DEPENDIENTE CUALITATIVA Y MODELOS DE VARIABLE DEPENDIENTE LIMITADA EJERCICIO 1 A- Una investigación sobre el mercado laboral de las mujeres en Uruguay ha prestado especial atención al grado de dedicación de la población económicamente activa femenina. Así, se ha optado por modelizar econométricamente la decisión de participar en forma de "tiempo completo" o en "tiempo parcial". Para ello se optó por ajustar un modelo logit cuya variable dependiente fue precisamente una variable Y dicotómica (tiempo completo=1, tiempo parcial=0). SE PIDE: 1) Indicar las razones por las cuales se juzgó utilizar un modelo logit y no un modelo clásico. 2) Indicar por qué no se opta generalmente por un modelo de probabilidad lineal. 3) ¿Qué forma funcional tiene la probabilidad (Pi) en los modelos logit y cuál es el sentido que tiene la misma? ¿Y en el modelo probit? B- La investigación arrojó los siguientes resultados (modelo logit): X β̂ = 3,640 - 0,434. X 1 - 0,143. X 2 + 0,053. X 3 - 0,287. X 4 - 0,1. X 5 (6,3) (-5,3) (-2,66) (0,71) (-1,9) (-6,9) donde: X1= educación en años de estudio X2= cantidad de menores de 14 años en el hogar X3= número de inactivos en el hogar X4= categoría de la ocupación (0= sector público, 1= sector privado) X5= tipo de ocupación ordenada de mayor a menor ingreso. Los valores entre paréntesis es el valor de t. Por otra parte se sabe: a) que ln L(Ω)= -826.99 b) el número de observaciones fue de 1789 mujeres activas. c) el R2 fue de 0.56 d) Si se hace el mismo modelo pero únicamente con la constante (sin variables explicativas) se observa que el logaritmo neperiano de la función de verosimilitud nueva es de ln L(ω)= -2345.4 e) las medias de las variables son: X 1 = 9 X 2 = 1,8 X 3 = 2 X 4 = 0,7 X 5 = 7,8 SE PIDE: 1) ¿Qué método de estimación se utilizó para este modelo si entendemos que el investigador no se equivocó? 2) ¿Cómo juzga Ud. este modelo a la luz de los resultados obtenidos? 3) ¿Cómo se interpreta el coeficiente de X2? EJERCICIO 2 A partir de una encuesta de marketing sobre consumo de bebidas light se observó que de 100 personas encuestadas, (57 mujeres y 43 hombres), el 63% prefería esta categoría de bebidas a las tradicionales. Esta preferencia resultó ser sensiblemente superior entre las consumidoras mujeres, de las 57 encuestadas, 45 respondieron afirmativamente. Contrariamente, entre los 43 encuestados de sexo masculino, sólo 18 manifestaron preferirlas. Para analizar esta comportamiento particular se especificó el modelo econométrico siguiente: F(X, a0 , a1 ) = P(Y = 1) = 1 1 + exp(- a0 - a1* SEXO) donde, Y=1 si el individuo prefiere las bebidas light Y=0 en el caso contrario. SEXO=1 si sexo femenino SEXO=0 si sexo masculino A partir de los datos de la encuesta realizada sobre una muestra de 100 individuos, se estimaron por el método de máxima verosimilitud los parámetros del modelo anterior, y en una segunda etapa se estima el modelo restringido, donde a1=0, obteniendo los resultados siguientes: [1] Modelo sin restricción coef. Variable Estim. Err.Std. a0 Constante -0.328 0.031 a1 SEXO 1.650 0.448 ln L= ln(LH)= -58.568 [2] Modelo con restricción a1=0 coef Variable b0 Constante Estim.Err.Std. 0.53220.207 En este caso el log de la función de verosimilitud se define como: 100 100 ln (LH) = ∑ i =1 y i * ln F ( b 0 ) + ∑ (1 - y i ) * ln [1 - F( b 0 )] i=1 SE PIDE: (a) Analizar los resultados de la estimación en [1] explicitando la significación estadística y la interpretación de los estimadores. (b) Calcular ln[LH] para el modelo [2] y verificar la validez de la restricción a1=0. (c) Mostrar que en el caso del modelo lineal Y= b0 + b1*X + u, donde Y es una variable binaria y el residuo u tiene media 0, éste es heteroscedástico. Explicitar los problemas de estimación y de formulación que se presentan. EJERCICIO 3 Se busca analizar los factores que diferencian a las empresas exportadoras dinámicas, a partir de una muestra de 100 firmas exportadoras. Se propone estimar el modelo logit siguiente: [1] P(Y = 1) = F(X, β ) = 1 1 + exp(-X.β ) donde Y=1, si la empresa es dinámica; Y=0, si la empresa no lo es. X , vector de variables que identifican la estrategia de la empresa; β: vector de parámetros. Los resultados obtenidos de la estimación por máxima verosimilitud son los siguientes: Ln(Verosimilitud)= ln[LH]= -12.78 Coef. Variable β0 β1 β2 β3 β4 β5 Coef.Estim. Constante Flex (var.binaria) Ps.Prd(var.continua) Ps.Tec(var.continua) Acuerdos (var.binar) % Región (var.cont.) -4.052 2.518 0.012 0.211 2.605 -1.042 Err.Std. T-Stat 1.727 1.442 0.006 0.103 1.430 0.573 -2.346 1.741 2.005 2.045 1.821 -1.818 donde: * Flex=1 si la empresa tiene una estructura de producción flexible, en caso contrario Flex=0. * Ps.Prd, Ps.Tec: representa el total de personal de producción y personal técnico respectivamente. * Acuerdos=1, si la empresa inició su actividad exportadora motivada por las preferencias otorgadas por los acuerdos comerciales con los países de la Región. * % Región: representa el % de las exportaciones de la firma a la Región (Brasil y Argentina) en el total de sus exportaciones. En una segunda etapa se estimó el modelo [1] imponiendo las siguientes restricciones al modelo inicial [2] β1=β2=β3=β4=β5=0. La estimación del modelo con restricciones por máxima verosimilitud, da como resultado: ln L[LH]= -23.05 SE PIDE: 1)Explicite las ventajas del modelo logit sobre el modelo de probabilidad lineal. 2) Analizar los resultados presentados y verificar la validez de las restricciones [2]. EJERCICIO 4 Se desea explicar los determinantes de que llevan a los trabajadores de una rama a sindicalizarse o no, para lo cual se estima un modelo logit siguiente en base a una encuesta a 595 trabajadores (valores de t entre paréntesis): ln [Pi/(1-Pi)] = 2.734 - 0.74 EXP -0.68.EDU - 0.483.SEX + 1.038. OCUP + (3.27) (-1.15) (-1.93) (-1.85) (6.27) 0.114.MANUF + 0.247. ESTCIV + 0.567. LUGRES. (1.96) (1.68) (2.34) donde: EXP: experiencia en años en el trabajo. EDU: años de educación. SEX: variable dummy con 1= mujer y 0= hombre OCUP: variable dummy con 1= ocupaciones manuales y 0= no manuales. MANUF: variable dummy con 1= rama industrial manufacturera, 0= otro caso. ESTCIV: variable dummy con 1= casado o unido y 0 otro caso. LUGRES: variable dummy con 1= residencia en Montevideo y 0 en el resto. Se sabe además que: (i) el logaritmo de la función de verosimilitud en la estimación anterior dio -312.37 (ii) el pseudo R2 de McFadden fue calculado en 0.201 (iii) el logaritmo de la función de verosimilitud de la estimación sin considerar las variables LUGRES ni MANUF fue -410.34 SE PIDE: a) Comentar la calidad y razonabilidad de cada variable del modelo completo anteriormente presentado, indicando las propiedades de los estimadores utilizados. b) Indique cómo calcularía el efecto marginal en la probabilidad de sindicalización de la variable LUGRES (por ejemplo, cúanto cambiaría y en qué sentido la probabilidad de sindicalizarse de un trabajador que se muda a Montevideo). c) Pruebe la hipótesis (al 5%) de que las variables LUGRES y MANUF son significativas conjuntamente, indicando claramente hipótesis nula, región crítica y decisión tomada. EJERCICIO 5 Se realiza en una ciudad un estudio para estudiar los factores explicativos de la decisión de los consumidores por seleccionar el crédito más barato antes de hacer una compra. Al respecto se observa que el consumidor no siempre hace una búsqueda previa y así muchas veces no compara entre créditos del proveedor o bancarios. Para modelizar el problema se consideran las siguientes variables: FUENTE: variable dummy con 1= si el consumidor seleccionó el crédito más barato, 0= en caso contrario ALTOC: dummy 1= el consumidor incurrió en altos costos al buscar el crédito más barato, 0= en caso contrario. ANTES: dummy 1= el consumidor utilizó previamente la fuente de crédito elegida, 0= en caso contrario. TAMANO: tamaño del crédito en una escala de 1 a 6, en orden creciente. INGRESO: ingreso del consumidor. RECHANT: dummy 1= el consumidor tuvo rechazos anteriores a solicitudes de crédito, 0= en caso contrario. RECHHOY: dummy 1= el consumidor es rechazado en esta solicitud de crédito, 0= en caso contrario. SANCION: dummy 1= el consumidor teme a las sanciones por incumplimiento, 0= en caso contrario. LUGAR : dummy 1= el consumidor vive en la ciudad del otorgante, 0= en caso contrario. A los efectos de modelizar la decisión de seleccionar o no el crédito más barato de plaza, se plantea el siguiente modelo: LS // Dependent Variable is FUENTE SMPL range: 1 100 Number of observations: 100 ======================================================================== VARIABLE COEFFICIENT STD. ERROR T-STAT. 2-TAIL SIG. ======================================================================== C 0.2705197 0.1313461 2.0595949 0.0423 ALTOC 0.0739448 0.1943647 0.3804435 0.7045 ANTES 0.2912300 0.0893644 3.2589030 0.0016 TAMANO 0.0546167 0.0231947 2.3547061 0.0207 INGRESO 6.399E-06 3.890E-06 1.6449111 0.1034 RECHANT -0.0860358 0.1038707 -0.8282970 0.4097 RECHHOY 0.0120319 0.1690905 0.0711566 0.9434 SANCION 0.0694218 0.1924804 0.3606696 0.7192 LUGAR 0.0978643 0.1051313 0.9308768 0.3544 ======================================================================== R-squared 0.221826 Mean of dependent var 0.710000 Adjusted R-squared 0.153416 S.D. of dependent var 0.456048 S.E. of regression 0.419610 Sum of squared resid 16.02259 Log likelihood -50.33533 F-statistic 3.242562 Durbin-Watson stat 1.554376 Prob(F-statistic) 0.002722 ======================================================================== Como se observa que algunas variables no son muy significativas se opta por un modelo más parco cuya salida se presenta a continuación: LS // Dependent Variable is FUENTE SMPL range: 1 100 Number of observations: 100 ======================================================================== VARIABLE COEFFICIENT STD. ERROR T-STAT. 2-TAIL SIG. ======================================================================== C 0.2637668 0.1088323 2.4236080 0.0173 ALTOC 0.0538265 0.1898632 0.2835017 0.7774 ANTES 0.2968236 0.0872215 3.4031022 0.0010 TAMANO 0.0564739 0.0227219 2.4854390 0.0147 INGRESO 6.466E-06 3.665E-06 1.7642790 0.0809 ======================================================================== R-squared 0.206925 Mean of dependent var 0.710000 Adjusted R-squared 0.173533 S.D. of dependent var 0.456048 S.E. of regression 0.414594 Sum of squared resid 16.32941 Log likelihood -51.28373 F-statistic 6.196737 Durbin-Watson stat 1.467090 Prob(F-statistic) 0.000179 ======================================================================== PARTE A SE PIDE: a.1) Comente sobre la modelización realizada indicando las ventajas inconvenientes de plantear el modelo de la manera en que fue realizado. e a.2) Compare los modelos anteriores utilizando un test asintótico conveniente. Dado que los inconvenientes de la anterior modelización fueron considerados excesivos, se opta por un modelo logit, cuyas salidas se presentan a continuación: LOGIT // Dependent Variable is FUENTE SMPL range: 1 100 Number of observations: 100 Convergence achieved after 4 iterations ======================================================================== VARIABLE COEFFICIENT STD. ERROR T-STAT. 2-TAIL SIG. ======================================================================== C -1.5747465 0.7789884 -2.0215277 0.0462 ALTOC 0.6740321 1.5122936 0.4457019 0.6569 ANTES 1.6300818 0.5205796 3.1312824 0.0023 TAMANO 0.3995130 0.1664400 2.4003422 0.0184 INGRESO 4.167E-05 2.439E-05 1.7084777 0.0910 RECHANT -0.4845424 0.5624051 -0.8615541 0.3912 RECHHOY -0.0992501 0.8994445 -0.1103459 0.9124 SANCION 0.3625645 1.1195969 0.3238349 0.7468 LUGAR 0.6280505 0.6559669 0.9574424 0.3409 ======================================================================== Log likelihood -47.708822 Cases with FUENTE = 1 71 Cases with FUENTE = 0 29 ======================================================================== LOGIT // Dependent Variable is FUENTE Date: 11-30-1997 / Time: 19:10 SMPL range: 1 100 Number of observations: 100 Convergence achieved after 2 iterations ======================================================================== VARIABLE COEFFICIENT STD. ERROR T-STAT. 2-TAIL SIG. ======================================================================== C 0.8953840 0.2203513 4.0634381 0.0001 ======================================================================== Log likelihood -60.215168 Cases with FUENTE = 1 71 Cases with FUENTE = 0 29 ======================================================================== PARTE B: b. 1) Estime la probabilidad de que una persona que no tuvo costos elevados de búsqueda, que utilizó la actual fuente de préstamo previamente, con un monto solicitado de crédito en una escala de 4, con $25000 de ingreso, sin antecedentes de rechazos previos ni actuales, sin temores a sanciones y viviendo en la ciudad del proveedor de crédito, haya seleccionado el crédito más barato. b. 2) Calcule una medida de bondad del modelo logit estimado. b. 3) Plantee la forma de la función de verosimilitud que está implícita en la estimación anterior e indique cuál serían, a su juicio, los más útiles valores iniciales a dar a los parámetros en la optimización de la misma. EJERCICIO 6 Se postula una relación teórica entre una variable y*: y* = β1 + β2.x2 + u. Al contrastarlo empíricamente, se sabe que la variable y* es censurada y, en realidad, se observa sólo sí es mayor o igual a cero. Por ello se opta por estimar un modelo tobit, para lo cual se observan 20 observaciones y se redefine el modelo teórico así: y = y* si y* ≥ 0 = 0 en otro caso Para estimar el modelo tobit se cuenta con la siguiente información: y x2 y x2 0 0 0 0 3.1348 3.508 0.8312 8.0064 0 0 1 2 3 4 5 6 7 8 9 10 3.9048 6.5144 5.9772 3.726 10.4124 16.9064 9.2968 7.8916 14.2164 2.9352 12 13 14 15 16 17 18 19 20 11 Al estimarlo se utiliza el software LIMDEP 7.0 del cual surgen las siguientes salidas: --> TOBIT;Lhs=Y;Rhs=ONE,X2$ +-----------------------------------------------------------------------+ | Limited Dependent Variable Model - CENSORED Regression | | Ordinary least squares regression Weighting variable = none | | Dep. var. = Y Mean= 4.863080000 , S.D.= 4.999494698 | | Model size: Observations = 20, Parameters = 2, Deg.Fr.= 18 | | Residuals: Sum of squares= 465.0228905 , Std.Dev.= 5.08278 | | Fit: R-squared= .020807, Adjusted R-squared = -.03359 | | Model test: F[ 1, 18] = .38, Prob value = .54403 | | Diagnostic: Log-L = -59.8423, Restricted(b=0) Log-L = -60.0526 | | LogAmemiyaPrCrt.= 3.347, Akaike Info. Crt.= 6.184 | +-----------------------------------------------------------------------+ +---------+--------------+----------------+--------+---------+----------+ |Variable | Coefficient | Standard Error |b/St.Er.|P[|Z|>z] | Mean of X| +---------+--------------+----------------+--------+---------+----------+ Constant 4.399890411 1.3611271 3.233 .0012 X2 .2988319928E-01 .48319808E-01 .618 .5363 15.500000 Normal exit from iterations. Exit status=0. +---------------------------------------------+ | Limited Dependent Variable Model - CENSORED | | Maximum Likelihood Estimates | | Dependent variable Y | | Weighting variable ONE | | Number of observations 20 | | Iterations completed 4 | | Log likelihood function -51.19597 | | Threshold values for the model: | | Lower= .0000 Upper=+infinity | +---------------------------------------------+ +---------+--------------+----------------+--------+---------+----------+ |Variable | Coefficient | Standard Error |b/St.Er.|P[|Z|>z] | Mean of X| +---------+--------------+----------------+--------+---------+----------+ Primary Index Equation for Model Constant 2.773231770 1.8644910 1.487 .1369 X2 .5410185033E-01 .62094804E-01 .871 .3836 15.500000 Disturbance standard deviation Sigma 6.429371360 1.3031508 4.934 .0000 SE PIDE: 1) Analice la pertinencia de la utilización del modelo tobit como método de estimación de una variable dependiente censurada. 2) ¿Qué hubiera cambiado del análisis anterior si usáramos un modelo de variable dependiente truncada? 3) Analice las salidas de LIMDEP evaluando el modelo tobit y el modelo estimado por MCO. EJERCICIO 7 Se desean analizar los determinantes del ingreso per cápita de los hogares que se encuentran bajo la línea de pobreza en Uruguay. Para ello, se plantea el trabajo con una muestra de 350 hogares calificados previamente como "pobres". El modelo planteado es: yi = β0 + β1.X1i + β2.X2i + β3.X3i + β4.X4i + β5.X5i + ui donde: y = log del ingreso per cápita del hogar (yi > línea de pobreza) X1 = años de educación del jefe del hogar X2 = sexo del jefe del hogar (variable dummy 1=hombre, 0=mujer) X3 = variable dummy de actividad del jefe (1=ocupado, 0=no ocupado) X4 = cantidad de perceptores de ingreso en el hogar X5 = rama de actividad del jefe (1= servicios y comercio, 0= otras). SE PIDE: 1) Indicar si el método de los MCO es apropiado para encarar la estimación del modelo planteado. En caso de no serlo, describa el método más apropiado para proceder fundamentando la razón en un sentido u otro. 2) Suponiendo que se estimó el modelo utilizando el mejor método de estimación en función del punto 1) se obtuvo el siguiente modelo estimado: yi = 0.324 + 1,724.X1 + 1,836.X2 + 0,107.X3 + 0,987.X4 + 1,234.X5 (0.23) (4.21) (8.31) (7.32) (12.43) (3.92) (Wald entre paréntesis) ln L(β) = -2252.36 Además, si se supone β1 = β2 = β3 = β4 = β5 = 0 y se estima nuevamente el modelo anterior, se obtuvo que: ln L(β) = -3886.58 De acuerdo a lo anterior, indique -utilizando la prueba de hipótesis que Ud. juzgue adecuada- si el modelo estimado es o no significativo al 95%. 3) Plantee la forma de la función de verosimilitud a maximizar en el modelo en caso de estimarlo por el método de máxima verosimilitud realizando los supuestos que Ud. juzgue necesarios. EJERCICIO 8 A los efectos de estudiar los factores explicativos de las horas trabajadas de las mujeres en Montevideo, se estimaron varios modelos que se complementan (son resultados ficticios): 1) un modelo probit explicativo de la tasa de actividad de las mujeres en función de características individuales de las mujeres y del hogar de pertenencia. 2) Un modelo de regresión lineal explicativo de su salario (ecuación salarial en el sentido de Mincer) incorporando como variable explicativa el llamado “sesgo de selección”. 3) Un modelo tobit explicativo de las horas trabajadas de las mujeres en función de características individuales y del hogar de origen. 4) Finalmente se realizó, para el modelo tobit, la descomposición de McDonald y Moffit a los efectos de contar con mayor poder explicativo de los resultados obtenidos. Los resultados resumidos fueron: 1) Modelo Probit Variable explicada: Y (1: activa; 0: inactiva) Variables explicativas: Coeficiente Constante 0.0443 Edad -0.0268 Educación 0.4156 Estado Civil -0.0958 Jefe (1,0) 0.7039 Ingr.total Del hogar sin muj. -0.0010 Otros ingresos -0.0007 Niños de 0 a 2 -0.3193 Niños de 3 a 5 -0.1192 Niños de 6 a 12 -0.0480 Serv.doméstico 0.8281 Cant.de desocup. 0.3604 Cant.de preceptores 0.4824 Log likelihood: -1250.7 Número de observaciones: 2624 t 0.14 -5.71 11.29 -2.58 4.66 -6.12 -4.13 -5.22 -2.04 -1.41 3.33 4.68 14.47 2) Ecuación Salarial con sesgo de selección (λ) Variable explicativa: W (salario por hora) Variables explicativas: Coeficiente Constante -1.96625 Edad 0.00581 Edad al cuadrado -0.0251 Educación 0.34989 Ingr.Total del hogar Sin la mujer 0.0034 λ 0.18828 t -16.82 2.428 3.21 15.66 4.189 2.238 R2 corregido: 0.48 3) Modelo tobit Variable explicativa: HRS (horas trabajadas) Variables explativas: Coeficiente Constante -6.822 Edad -0.2008 Educación 2.1532 Estado Civil -1.6448 Jefe 15.3362 Ingr.total del Hogar sin mujer -0.02830 Niños de 0 a 2 -0.00185 Niños de 3 a 5 -2.25421 Niños de 6 a 12 -0.96392 Serv.doméstico 1.2372 Número desocupados -18.089 Número de preceptores 11.1137 Salario de Reserva (W) 16.05272 t -1.026 -1.778 1.453 -1.64 5.072 -4.641 -3.835 -1.546 -1.1513 3.35 -9.834 14.41 2.019 Varianza estimada σ2: 1022.4 Log likelihood: -8264 Número de observaciones: 2624 (El salario de reserva surge de imputarle un salario a las mujeres que no son activas de acuerdo al modelo 2. 4) Descomposición de McDonald y Moffit: Calculada en la media de las variables, el 45.6% del efecto total se debe a cambios en las variables por encima de cero, es decir de cambios en el conjunto de variables explicativas en las horas trabajadas, sabiendo que ectivamente son activas. SE PIDE: a) Comente los resultados de los modelos. b) Explicite la forma del sesgo de selección λ y su significado. c) Explicite los componentes de la descomposición de McDonald y Moffit y su significado. d) Indique cómo estimaría el modelo tobit por el método bietápico de Heckman. ¿Qué relación guarda con lo realizado anteriormente?