重要なる三角公式
Anuncio

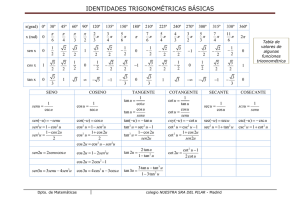
重要なる三角公式 sin A cos A 1 = cot A 平方関係: sin 2 A + cos 2 A=1 1+tan 2 A=sec2 A tan A= cos A 1 逆数関係: cot A= = sin A tan A cosec A= sec A= 1 cos A 1 sin A tan A = sin A= 1−cos 2 A = 1+tan2 A 1 1+cot2 A 1 = cos A= 1−sin 2 A = 1+tan2 A cot A 1+cot2 A 加法公式: sin (A+B) =sin A · cos B+cos A · sin B sin (A−B) =sin A · cos B−cos A · sin B cos (A+B) =cos A · cos B−sin A · sin B cos (A−B) =cos A · cos B+sin A · sin B tan (A±B) = tan A±tan B sin (A±B) , tan A±tan B= 1∓tan A · tan B cos A · cos B sin (B±A) cot A · cot B∓1 cot (A±B) = , cot A±cot B= sin A · sin B cot B±cot A sin 2 A−sin 2 B =cos 2 B−cos 2 A =sin (A+B) · sin (A−B) cos 2 A−sin 2 B =cos 2 B−sin 2 A 積を和ま たは差に かえる公 式: =cos (A+B) · cos (A−B) 1 1 sin A · sin B= cos (A−B) − cos (A+B) 2 2 1 1 cos A · cos B= cos (A−B) + cos (A+B) 2 2 1 1 sin A · cos B= sin (A+B) + sin (A−B) 2 2 cot A+cot B tan A+tan B tan A · tan B= cot A · cot B= tan A+tan B cot A+cot B 倍角公式: sin A=2 sin 1 1 A · cos A sin 2A=2 sin A · cos A 2 2 cos 2A=cos2 A−sin2 A=1−2sin2 A =2cos2 A−1 2 2tan A tan 2A= = cot A−tan A 1−tan2 A cot A−tan A cot2 A−1 tan 2A= = 2 2cot A 1 1 1−tan2 A 2tan A 半角公式: 2 2 sin A= cos A= 1 1 1+tan2 A 1+tan2 A 2 2 2sin2 A=1−cos 2A 2cos2 A=1+cos 2A