Document
Anuncio

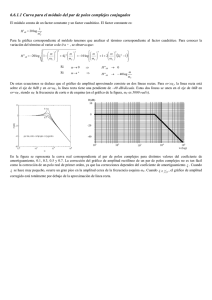
ANALISIS FRECUENCIAL Objetivos: Analizar un sistema en el espectro de frecuencias en régimen forzado. El espectro de frecuencia se logra excitando el sistema estable, con una función senoidal de amplitud Cte. y leyendo su respuesta de estado estacionario (Régimen Forzado).- Se hacen sucesivos ensayos, para obtener la respuesta variando la frecuencia de la excitación desde 0 a infinito. X= A sen wt y= Ymax sen(wt-ϕ) SISTEMA x Y A t Ymax t Aplicaciones: • Trazado de diferentes representaciones gráficas ( diagramas de Nyquist, Bode, Nychols, etc.) • Determinación de la estabilidad y estabilidad relativa en el diseño a bucle cerrado. • Reconstrucción de la función de transferencia a partir de los resultados del ensayo. Teorema • Sea F(s) la f. de T. de bucle abierto ( o cualquier función de s sobre la que se desea hacer el análisis frecuencial). La relación de amplitud ( cociente entre los módulos las funciones de salida y entrada, respectivamente) y el ángulo de desfase de entre ellas, son el módulo y el ángulo de desfase del complejo que se obtiene de sustituir s por jω en la F(s). Relación de amplitud => Desfasaje => [ ] F ( jω ) = F( s ) ϕ =arg([ F( s ) ] = s= J ω [ [ Y( j ω) X ( jω ) ℑ F( jω ) ) = tg s =J ω ℜ F( jω ) −1 ] ] Sea una función de transferencia genérica del tipo: K (1 + 2ς 1T1s + T1s )∏ 2 G( s ) = s (1 + 2ς 2T2 s + T s )∏ r 2 2 2 (1 + Ti s ) m i =1 n j =1 (1 + T j s ) e −τ s Por lo tanto los elementos que pueden componer la G(s) son: • +K ó -K constante con signo pos. O neg. •s ± r polo/Cero múl.(± r ) al origen • ( 1 + T s) ± n Binomio de orden ( ± n ) • [ 1 + 2ζTs + T2 s2] ± 1 Sist. de 2do Orden ( ± 1) • exp( - τ s) Tiempo muerto Diagrama de BODE El diagrama de Bode está constituido por dos gráficas: gráfica de relación de amplitud o de módulo: donde se representa la relación de amplitud (escala logarítmica) vs. la frecuencia (escala logarítmica), se puede expresar también en db = 20 log (RA) (escala lineal) vs. frecuencia (escala logarítmica) •gráfica de desfasaje: representando ángulo de fase vs. frecuencia. CASO 1: G(S) = K G(jw) = K Módulo = K ϕ= tg-1 (Im/Re) = 0 ϕ=Si (-K)= - 180 CASO 2-a: G(s) = s G(jw) = jw Mod = w ϕ = 90º CASO 2-b: G(s) = 1/s G(jw) = 1/jw Mod = 1/w ϕ = -90º Generalizando en el caso de polos multiples (± r ) al origen : Módulo = ω ±r CASO 3: Modulo = G(s) = (Ts+1) 1+(ωT ) 2 Fase = ωT tg −1 1 Modulo[dB] = 20 log 1+(ωT ) 2 Si: w << 1/T Módulo = 1 Fase 0º Si: w >> 1/T Mód. = 20 log wT = 20 log (T)+20 log (w) Fase 90 º Graficando módulo y fase, obtenemos: CASO 4: Modulo = G(s) = 1/(Ts+1) 1 1+(ωT ) 2 −1 − ωT tg Fase = 1 Llamando al módulo = p Para w => 0 w => Inf p = 1 => log(p) = 0 p = (1/Tw) => log(p) = -20log(T) - 20log(w) Considerando la fase: Para w => 0 w => Inf w=> 1/T ϕ => 0 ϕ => -90 º ϕ => -45 º Graficando módulo y fase, obtenemos: CASO 5: Para un sistema de segundo orden del tipo: 1 G (s) = 1 + 2ςTs + T 2 s 2 El módulo es: 1 (1 − T 2ω 2 ) 2 + (2ςTω ) 2 − 2ςω 2 2 1− T ω Su ángulo de fase es: ϕ = tg −1 Como podemos apreciar, tanto el módulo como el ángulo dependen de ζ, graficando para varios valores de ζ, obtenemos: Graficando el módulo para varios valores de ζ ( 0,1; 0,3; 0,5; 1 y 2) Apreciamos que a ζ < 0,7071 aparece un pico de resonancia ω r que ocurre a: ω r = ω n 1−2ς 2 siendo M r = 1 2 2ς 1 − ς Graficando la fase para varios valores de ζ ( 0,1; 0,3; 0,5; 1 y 2)