P O A A` B B`

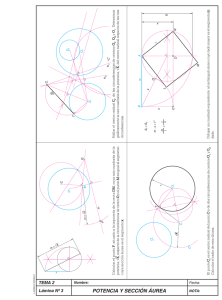
TANGENCIA I: APLICACIÓN DEL CONCEPTO DE POTENCIA.
POTENCIA: (Ilustración nº 1)
Es una transformación geométrica basada en la proporcionalidad inversa (dos magnitudes inversamente proporcionales son las que varían de tal forma, que su producto permanece constante, dichas magnitudes varían en
sentido inverso, si una aumenta, la otra disminuye y,
viceversa).
A'
A
O
P
La Potencia de un punto conocido P respecto de una
circunferencia dada de centro O es el producto constante
de los segmentos determinados por cualquier cuerda
trazada a la circunferencia desde dicho punto P.
B
B'
2
PA  PA’ = PB  PB’ = K (CONSTANTE)
• Cuando el punto P es exterior, la potencia será positiva. Los triángulos determinados por las secantes
trazadas desde P a la circunferencia (ABA’ y BAB’)
son semejantes, puesto que tienen un lado común
(AB) y dos ángulos iguales (ángulo AA’B = ángulo
AB’B). (Ilustración nº 1)
ILUSTRACIÓN Nº 1
A
• Cuando una de las secantes de trazadas desde un punto exterior (P) a una circunferencia dada de centro O
toma la posición límite (se transforma en una recta
tangente), A y A’ pasan a ser un solo punto (T). Los
triángulos PTB y PTB’ son semejantes, estableciéndose la siguiente relación de proporcionalidad:
PT / PB = PB’ / PT
2
B
A'
A'
O
P, A, B
ILUSTRACIÓN Nº 2
a
T
k
a
P
2
B'
La potencia será igual al cuadrado de la distancia
desde el punto exterior P al de tangencia (T)
T
k
P
La potencia será el cuadrado de la distancia del punto
exterior al centro de la circunferencia menos el radio de
la misma. PT2 = PD  PD’ = (m - n) (m + n) = m2 – n2.
2
2
PT = d - r . (Ilustración nº 3-b)
O
a
B
(Ilustración nº 3-a)
También se puede determinar la potencia considerando
el radio de la circunferencia y de la distancia del punto
exterior al centro.
B'
b
, es decir PT = PB  PB’ = k (constante)
2
O
P
• Cuando el punto P es interior de la circunferencia, la
potencia será negativa ya que los segmentos PB y PA
serán positivos y los segmentos PB’ y PA’ negativos.
(Ilustración nº 2-a)
• Cuando el punto P es concíclico (está contenido o
pertenece a una circunferencia o por él pasa una circunferencia única) de la circunferencia dada, su demostración es evidente puesto que las distancias PA y
PB son nulas por ser P, A y B el mismo punto, por
ello cualquier distancia (PA’, PB’…) multiplicada
por cero, es cero. (Ilustración nº 2-b)
B'
a
D
O
m
b
ILUSTRACIÓN Nº 3
D'
n
CONSTRUCCIÓN DE MEDIA PROPORCIONAL DE DOS SEGMENTOS APLICANDO POTENCIA
La media proporcional de dos segmentos es otro segmento tal que el
cuadrado de su distancia es igual al producto de los dos segmentos
dados. (Ilustración nº 4)
Anteriormente se ha resuelto este problema mediante la aplicación del
TEOREMA DEL CATETO o bien del TEOREMA DE LA ALTURA.
Ahora lo vamos a resolver aplicando el concepto de potencia.
Dados dos segmentos m y n de los cuales se pide determinar su media
proporcional, se disponen éstos superpuestos con uno de sus extremos
(P) común. A continuación se traza una circunferencia de diámetro el
segmento diferencia (m-r). La magnitud del segmento tangente PT = k
es la media proporcional buscada. PT2 = m  n = k2..
T
k
O
P
n
m
ILUSTRACIÓN Nº 4
CONSTRUCCIÓN DE “SECCIÓN ÁUREA” DE UN SEGMENTO APLICANDO POTENCIA
Sabemos que la Sección Áurea de un segmento es el resultado de dividir
un segmento en dos partes tales que una de ellas, la mayor de las dos, sea
media proporcional entre el segmento total y la otra, es decir que la mayor
al cuadrado es igual al producto de la menor con el segmento dado.
(Ilustración nº 5)
En un segmento s la sección áurea es x la otra será (s-x); de donde se
tendrá que verificar:
s
x

x ( s  x)
s (dato)
A
B
C
(s - x)
x
; o bien x² = s(s-x).
Al segmento x que cumple tal condición se le denomina segmento
áureo del segmento s dado.
Q
O
La definición de potencia vista anteriormente permitía trazar una circunferencia por el extremo B del segmento dado AB = s, con un diámetro perpendicular e igual a dicho segmento.
El segmento AP = x, obtenido al unir el extremo A con el centro O de
la circunferencia es el áureo del segmento s dado; verificándose:
P
x
A
AB² = AP  AQ: esto es: s² = x(s + x) = xs + x²,
C
x
(áureo de s)
de donde: x² = s² -xs = s(s-x).
También se demuestra que la parte menor del segmento (s-x) es el
áureo del segmento x (mayor que las dos partes de s).
(s - x)
B
(áureo de x)
m
ILUSTRACIÓN Nº 5
HAZ DE CIRCUNFERENCIAS QUE PASAN POR DOS PUNTOS (P y Q)
Lo forman todas las posibles circunferencias que pasan por todos los
T
puntos dados (P y Q); sus centros O1, O2, O3, … se encuentran en la
mediatriz del segmento PQ. La recta que une P con Q es secante
común a todas las circunferencias del haz. (Ilustración nº 6)
Desde cualquier punto exterior M, la potencia es la misma para todas
M
P
Q
las circunferencias (MT es constante), lo que significa que todos los
segmentos de tangentes trazados desde M al haz de circunferencias
son iguales.
T
ILUSTRACIÓN Nº 6