Regresión lineal múltiple. - Departamento de Matemática Aplicada y
Anuncio

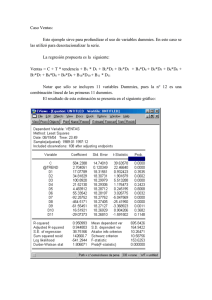
Departamento de Matemática Aplicada y Estadística Universidad Politécnica de Cartagena Curso 03/04 Ajuste por mínimos cuadrados (2) Seguimos con la práctica de regresión lineal múltiple con SPSS. Recordar que buscamos realizar ajustes por mínimos cuadrados para modelos lineales en los parámetros, es decir para el caso en que la relación entre la variable dependiente (también llamada variable respuesta) que nos interesa Y, y las variables explicativas (tambíen llamados regresores) X1, X2,..., Xk es Existen k parámetros constantes β1, β2,...,βk tales que Y=β1X1+β2X2+...+βkXk+ε donde ε es una perturbación aleatoria Hemos realizado observaciones del fenómemo: i.e conocemos para varias combinaciones de valores de las variables independientes cuál ha sido el valor de la variable respuesta. Queremos ajustar un modelo de tipo lineal a las observaciones de las que disponemos. El ajuste consiste en encontrar valores aproximados de los coeficientes β1, β2,...,βk. Regresión lineal múltiple. Para ilustrar los comandos necesarios, analizaremos el conjunto de datos correspondiente al problema siguiente: un ingeniero de producción es responsable de la reducción del costo. Uno de las materias primas fundamentales en la producción es el agua. Para estudiar el consumo de agua , el ingeniero apunta durante 17 meses el consumo mensual de agua (y) junto con los siguientes indicadores: la temperatura media mensual (x2 en ºF) la producción (x3 ), el número de días de trabajo en el mes (x4) y el número de personal en la planta de producción (x5). Los datos están en el fichero agua.txt. Después de haber importado los datos (comprobar que todas las variables han sido importadas como “numéricas”), pasamos al ajuste de los datos con un modelo Y=β1X1+β2X2+β3X3+ β4X4+β5X5+ε donde ε es una perturbación aleatoria normal con media cero y varianza,σ2 y X1=1 (término constante) Para ello, al igual que para la regresión lineal simple, utilizamos la instrucción Analizar>Regresión->Lineal. Ahora pasamos las cuatro variablesX2 a X5 en el cuadro de las variables independientes. En el submenu de opciones, podemos entre otras cosas decidir excluir el término constante en el modelo, lo que no haremos en este caso. Obtenemos Resumen del modelo Modelo R R R Error típ. de la cuadrado cuadrado corregida estimación 1 ,876 ,767 ,689 248,9641 a Variables predictoras: (Constante), X5, X4, X2, X3 Ib Ia Coeficientes Coeficientes no estandarizados Modelo 1(Constante ) X2 X3 X4 X5 a Variable dependiente: Y Coeficient es estandariz ados B Error típ. 6360,337 1314,392 13,869 ,212 -126,690 -21,818 II 5,160 ,046 48,022 7,285 III t Sig. 4,839 ,000 2,688 4,648 -2,638 -2,995 ,020 ,001 ,022 ,011 Beta ,419 1,671 -,415 -1,074 IV Los recuadros se interpretan de la siguiente manera. Recuadro Ia: Proporciona el valor de R2 que es el coeficiente de determinación múltiple que nos indica la proporción de la variabilidad en los datos explicada por el modelo de regresión. Recuadro Ib: Proporciona el valor de la desviación típica residual. Recuadro II En la columna Coefficientes no estandarizados podemos leer los valores obtenidos de los coeficientes, en la línea Constante, tenemos el coeficiente de X1=1 En este caso la ecuación proporcionada es Consumo promedio= 6360.4+13.9X2+0.2X3-126.7X4+21.8X5 Recuadro III: Proporciona los errores típicos de los estimadores de los coeficientes, los podríamos utilizar para construir intervalos de confianza. Recuadro IV: Sirve para determinar si los coeficientes de cada variable explicativa son significativamente distintos de 0: en la columna t, obtenemos los valores de los estadísticos de prueba asociados a cada coeficiente, mientras que en la columna Sig, podemos encontrar los p-valores de las pruebas H0 : βi=0 contra H1 : βi≠0, para cada uno de los coeficientes. En este caso todos los p-valores son pequeños, lo que implica que nos quedamos con todas las variables en el modelo. Podemos realizar con SPSS intentos de construcción de modelos. En particular podemos llevar a cabo la eliminación hacia atrás, seleccionando en el cuadro de diálogo abierto con la instrucción Analizar->Regresion->Lineal, el método “Hacia atrás”. En el cuadro Opciones, podemos fijar el valor del umbral del p-valor que fijamos para que una variable sea eliminada del modelo, cambiando el valor en “Salida”. Por defecto aparece un valor del umbral de 0.1. Continuamos y aceptamos para obtener la secuencia de modelos en los que posiblemente vayan siendo las variables eliminadas una por una hasta dar con el modelo final. En este caso puesto que todos los p-valores son menores que 0.1, el algoritmo se para en la primera iteración. Ejercicios Volumen de madera. En ingeniería forestal existe la necesidad evidente de poder predecir el volumen de madera disponible de un tronco de un árbol todavía en pie. El método más sencillo consiste en medir el diámetro cerca del suelo y la altura del tronco y estimar el volumen utilizando estas dos cantidades. En el fichero cerezos.txt están los datos de un experimento realizado en un parque nacional de Pennsylvania donde se midió con cuidado el volumen después de cortar el tronco de ( v: volumen, d: diámetro y a: altura) 1. Realizar el análisis de regresión lineal del volumen sobre el diámetro y la altura. 1. Proceda al análisis de los residuos, ¿Cuál es su diagnóstico? 2. Si se supone que el tronco es un cilindro perfecto, ¿ cuál sería la relación entre v,a y d ? Proponer una transformación sobre los datos que sea acorde con esta relación física Realizar el ajuste lineal correspondiente con especial interés en el análisis de los residuos. 3. Si se supone que el tronco es un cono perfecto, \¿ cuáles deberían ser los valores de los parámetros del apartado anterior?. Consumo de helados Se quisó identificar los factores más influyentes en el consumo de helados. Para ello se midió en una familia durante 30 semanas entre el 18 de marzo de 1953 hasta 11 de julio 1953 el consumo semanal de helado por persona (y), junto con las cantidades siguientes que se pensaba podían tener alguna influencia sobre el consumo : p el precio de una pinta de helado, i los ingresos semanales de la familia, temp : la temperatura media de la semana. También aparece el número de la semana. Los datos están en el fichero helados.dat 1. Represente gráficamente el consumo de helados en función de las semanas. 2. Determinar la matriz de correlación de las variables y,p,i y temp. Para ello se utiliza la opción Analizar->Correlaciones->bivariadas, y como es usual en SPSS pasamos desde la lista de las variables de la izquierda las variables que nos interesan. ¿Cuál es la variable que parece tener más influencia en y? 3. Realizar un ajuste lineal de y sobre p,i y temp. ¿Qué vale la varianza residual y R^2? 4. Realizar un ajuste lineal de y sobre i y temp. Misma pregunta que en el apartado anterior 5. Guarde los valores ajustados en una variable llamada ajucomp. Represente en la misma gráfica y en función de semanas y ajucomp en función de semana. Calor emitido por el fraguado de cemento. Se estudia la relación entre la composición de un cemento tipo Portland y el calor desprendido durante la fase de fraguado1. Los datos se pueden encontrar en el fichero hald.txt. La variable Y es la cantidad de calor desprendido en calorías por gramos de cemento, mientras que las variables X1, X2 X3 y X4 representan el contenido en porcentaje de cuatro productos A, B, C y D. 1. Obtener la matriz de correlaciones de las distintas variables. 2. Realizar un ajuste lineal utilizando el procedimiento de eliminación hacia atrás. Perdida de peso de un producto Se sabe que un determinado producto pierde peso después de ser producido. En el archivo peso.txt se ha recogido la diferencia (peso nominal-peso real) para varias unidades en distintos tiempos. 1. Ajustar un modelo de regresión lineal simple para explicar la evolución de la diferencia de peso en función del tiempo. 2. Realizar la gráfica de los residuos en función de los valores ajustados. ¿Le parece adecuado nuestro modelo para analizar estos datos? ¿Tiene alguna idea para mejorarlo? 3. Realizar el ajuste por un polinomio de orden 2. 1 Fuente: A. Hald, Statistical Theory with Engineering Applications, Wiley, New York, 1952, p. 647