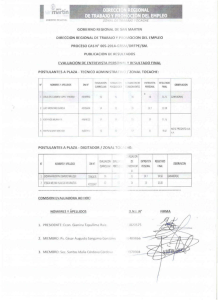
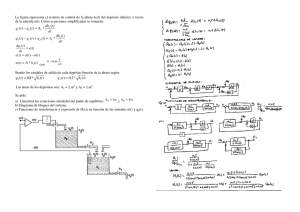
el director del proyecto - IIT - Universidad Pontificia Comillas
Anuncio

Autorizada la entrega del proyecto de la alumna: D.ª Nuria Merchán Ríos Madrid, 8 de septiembre de 2009 EL DIRECTOR DEL PROYECTO Fdo.: Dr. D. Francisco Javier Rodríguez Gómez Vº Bº del Coordinador de Proyectos Fdo.: D. Eduardo Alcalde Lancharro Fecha: ……/ ……/ …… UNIVERSIDAD PONTIFICIA COMILLAS ESCUELA TÉCNICA SUPERIOR DE INGENIERÍA (ICAI) INGENIERO EN INFORMÁTICA PROYECTO FIN DE CARRERA SOFTWARE DE RESOLUCIÓN DE PROBLEMAS CON VALOR EN FRONTERA DE ECUACIONES DIFERENCIALES ORDINARIAS AUTORA: NURIA MERCHÁN RÍOS MADRID, SEPTIEMBRE 2009 Software para la resolución de EDO I Agradecimientos y dedicatoria “Sé perseverante, porque el agua horada la roca a fuerza de caer sobre ella. Prosigue y no desmayes, y ten en mucho lo poco conseguido, pues la llovizna no es abundante y, sin embargo, cala.” El collar de la paloma, Ibn Hazm de Córdoba Gracias a mis padres y a mi hermana que siempre han estado ahí apoyándome y recordándome esta cita de este poeta cordobés. También quiero darle las gracias a mi director Francisco Javier, por su ayuda y paciencia. Finalmente, quiero dedicarle este proyecto, de forma muy especial a aquellos que se emocionarían sabiendo que ya terminé esta ingeniería. Proyecto Fin de Carrera II Resumen Es objeto del presente proyecto el abordar un desarrollo software para el estudio, análisis e implementación de los métodos numéricos que se encargan de resolver de manera aproximada las ecuaciones diferenciales de segundo orden con la siguiente estructura: y≥ = f Hx, y, y£ L a§x§b que verifica las condiciones de frontera en los puntos extremos del intervalo: yHaL = a y yHbL = b. Este tipo de ecuaciones diferenciales de segundo orden se presentan con frecuencia en numerosos problemas de Ingeniería Civil (deflexiones de una viga de sección rectangular con carga uniforme), en Física (potenciales electroestáticos en materiales cargados uniformemente), y en Química (análisis del flujo de la corriente en un tubo al vacío, ecuación de Van der Pol). Los métodos numéricos objeto de análisis, estudio e implantación son: 1.- Método del disparo lineal. Se basa en la sustitución del problema lineal con condiciones de frontera por otros dos problemas con valores iniciales. Se emplea el método de RungeKutta de cuarto orden (que resuelve ecuaciones diferenciales de primer orden) con el fin de conseguir las aproximaciones de este método. Software para la resolución de EDO III 2.- Método del disparo para problemas no lineales. Aun pareciéndose al método lineal, la solución del problema no se expresa como una combinación lineal de las soluciones a los problemas de dos valores iniciales, si no que utiliza una sucesión de problemas con valor inicial. Este método se auxilia del método de de Runge-Kutta de cuarto orden y del método de resolución de ecuaciones no lineales de Newton. 3.- Método de las diferencias finitas para problemas lineales. Este método reemplaza las derivadas en las ecuaciones diferenciales por una aproximación de cocientes de diferencias finitas adecuadas. 4.- Método de las diferencias finitas para problemas no lineales. Utiliza, como en el método anterior, el método de diferencias finitas, pero al dar origen a un sistema de ecuaciones no lineales, se requiere un proceso iterativo para su resolución, en particular se emplea el método de Newton para sistemas de ecuaciones no lineales. 5.- Método de Raileigh-Ritz. En este método se selecciona de un conjunto de todas las funciones, suficientemente derivables que verifican las condiciones de frontera, aquellas que reducen al mínimo unas determinadas integrales. Posteriormente, se disminuye el conjunto de funciones candidatas para obtener la aproximación a la solución del problema con valor de frontera. Es decir, la función que aproxima la solución es una combinación lineal de ciertas funciones básicas que son linealmente independientes. En el método lineal segmentario cada función básica es sustituida por un polinomio lineal definido por intervalos. Proyecto Fin de Carrera IV En el método de los trazadores cúbicos cada función básica es sustituida por un polinomio cúbico o trazador B (polinomio cúbico en forma de campana). Este método da origen a un sistema lineal de ecuaciones con una matriz simétrica de banda con un ancho máximo de valor siete, que se resuelve mediante el método de descomposición de Cholesky. Los citados métodos, tras haberse estudiado detalladamente, se diseñan y se programan en un lenguaje con capacidades de cálculo numérico, simbólico y con funcionalidades gráficas, a fin de analizar tanto las aproximaciones numéricas con su cota de error, como representar las gráficas de la solución exacta de la ecuación diferencial junto a la función aproximada obtenida. Por ultimo, se presentan todos los algoritmos de este proyecto bajo una interfaz gráfica de usuario (GUI) que facilita y permite comprobar cada uno de los métodos para cualquier ecuación diferencial de segundo orden con valor en la frontera de dos puntos. Los resultados, numéricos y gráficos, se presentan en la propia interfaz de usuario diseñada, y el detalle de todos los pasos intermedios con los sistemas de ecuaciones lineales y no lineales y demás fórmulas, se indican en un fichero del entorno de desarrollo empleado: el programa Mathematica. Software para la resolución de EDO V Abstract The objective of this project is to develop software for the study, analysis and implementation of numerical methods which are used to solve in an approximate way a second-order differential equations with the following structure: y≥ = f Hx, y, y£ L a§x§b Which verifies the boundary-values conditions at the endpoints of the interval: yHaL = a y yHbL = b. This types of second-order differential equations are often presented in many problems of Civil Engineering (alterations of a rectangular beam section with uniform weight load) in Physics (electrostatic potentials in materials uniformly loaded) and in Chemistry (The Van der Pol equation, i.e. an analysis of the flow of the stream in a vacuum pipe/tube (Relaxation Oscillations). The numerical methods to be analysed, studied and implanted/introduced are: 1. - Linear shooting method. Which is based on the substitution of the boundary-value linear problem for two other problems with initial values. The fourth-order Runge-Kutta method (which solves first-order differential equations) with the aim of achieving the approximations of this method. Proyecto Fin de Carrera VI 2. - The shooting method for nonlinear problems. Even though it is similar to the linear method, the solution to the problem is not expressed as a linear combination of the solutions to the problems with two initial values Instead a succession of problems with initial value is used. This method is supported by the fourth-order Runge Kutta method and the Newton method for solving nonlinear equations. 3. - The finite-difference method for linear problems. This method replaces the derivatives in the differential equations for an approximation of quotients of adequate finite differences. 4. - The finite-difference method for nonlinear problems. Like the previous method, it uses the finite-difference method, but as it gives rise to a system of nonlinear equations, a repeated process is required in order to solve it; in particular the Newton method for nonlinear equations systems is applied. 5. - Raileigh-Ritz method. In this method, a whole group of all the functions is selected, enough derivative, which verify the boundary-values conditions, those ones that reduce some specific integral signs to the minimum. As a result, the group of candidate functions for obtaining the approximation to the solution of the problem with boundary-value is diminished. That is to say, the function which brings up the solution is a linear combination of some basic functions which are independent in a linear way. The piecewise linear method, each basic function is substituted by a linear polynomial defined by intervals. In the cubic spline method, each basic function is substituted by a cubic polynomial or B Software para la resolución de EDO VII tracer (cubic polynomial with a bell shape). This method gives rise to a linear system of equations with a symmetric band matrix with a maximum width of seven which is solved through Cholesky's decomposition method. When studied in detail, the methods mentioned above are designed and programmed in a language with numerical, symbolic calculation capacities and with graphic functions with the aim of analysing the numerical approximations with their error figure, and also representing the exact graphics solution of the differential equation together with the approximate function obtained. Finally, all the algorithms of this project under a graphical user interface (GUI) facilitates and allows checking each of the methods for any second-order differential equation with boundary-value of two points. The numerical and graphic results are presented in the designed user interface itself, and the detail of all the intermediate steps with the linear and nonlinear equation system together with the rest of the formula are shown in a file of the development environment used: the Mathematica programme. Proyecto Fin de Carrera VIII Índice Agradecimientos y dedicatoria ...................................................................................... I Resumen......................................................................................................................... II Abstract........................................................................................................................... V Índice..............................................................................................................................VIII 1. Introducción y motivación.......................................................................................... 1 2. Objetivos del proyecto................................................................................................ 5 3. Análisis de requisitos.................................................................................................. 7 3.1. Requisitos funcionales...................................................................................... 7 4. Metodología................................................................................................................ 13 5. El método del disparo lineal....................................................................................... 20 5.1. Método de Runge-Kutta................................................................................... 20 5.2. Método del disparo lineal................................................................................. 24 6. El método del disparo no lineal.................................................................................. 30 7. El método lineal de diferencias finitas....................................................................... 38 8. El método lineal de diferencias finitas para problemas no lineales............................ 45 9. El método de Rayleigh-Ritz....................................................................................... 54 9.1. Método lineal segmentario de Rayleigh-Ritz................................................... 54 9.2. Método de trazadores cúbicos de Rayleigh-Ritz.............................................. 72 9.2.1. Método de Cholesky............................................................................... 93 10. Estudio de la arquitectura......................................................................................... 95 11. Diseño externo.......................................................................................................... 96 11.1. Métodos lineales............................................................................................. 97 Software para la resolución de EDO IX 11.2. Métodos no lineales........................................................................................103 11.3. Métodos de Rayleigh-Ritz..............................................................................110 11.4. Menú Ayuda...................................................................................................131 12. Valoración económica y planificación....................................................................133 12.1. Valoración económica del proyecto...............................................................133 12.2. Planificación temporal del proyecto...............................................................138 13. Conclusiones.............................................................................................................139 Anexo I. Manual de Instalación y de Usuario.................................................................143 Bibliografía.....................................................................................................................146 CD-ROM. Software de Resolución de Problemas con valor en frontera para la Resolución de Ecuaciones Diferenciales Ordinarias. (en Mathematica” ). † Código de los algoritmos numéricos. Código (Problemas de Contorno con Ecuaciones Diferenciales Ordinarias).nb † Interfaz de usuario. Interfaz.nb † Conjunto de problemas de Ecuaciones Diferenciales Ordinarias resueltos con los diferentes métodos numéricos de aproximación. Problemas (Problemas de Contorno con Ecuaciones Diferenciales Ordinarias).nb Software para la resolución de EDO 1 1. Introducción y motivación La construcción de infraestructuras de gran tamaño y para uso público, principalmente edificios, obras hidráulicas y de transporte, es hoy en día de gran importancia. Por ello, existe una rama de la ingeniería llamada Ingeniería Civil que aplica los conocimientos de Física, Química y Geología a la elaboración de dichas infraestructuras. Puente Valdebebas HMadridL. Figura 1 Croquis del puente Valdebebas HMadridL. Figura 2 Proyecto Fin de Carrera 2 Un problema común en las obras de ingeniería civil, como la que se puede observar en las imágenes anteriores, es el que se relaciona con la deflexión de una viga de sección transversal rectangular sujeta a una carga uniforme, mientras sus extremos están soportados de modo que no experimentan deflexión alguna. Deflexión de una viga. Figura 3 La ecuación diferencial que aproxima esta situación física es una ecuación diferencial de segundo orden de la forma „2 w „x2 = S EI w+ qx 2EI Hx - 1L donde w = w HxL es la deflexión a una distancia x desde el extremo izquierdo de la viga, l es la longitud, q representa la intensidad de la carga uniforme, E es el módulo de elasticidad, S el esfuerzo en los extremos y finalmente I es el momento central de inercia. Esta ecuación diferencial tiene asociadas dos condiciones de frontera dadas por la suposición de que no ocurre deflexión alguna en los extremos de la viga w H0L = w HlL = 0. Software para la resolución de EDO 3 Cuando la viga tiene un espesor uniforme, el producto E I es constante y la solución exacta se obtiene fácilmente. No obstante, en muchas aplicaciones el espesor no es uniforme y, por lo tanto, el momento de inercia I es una función de x, y se requieren métodos de aproximación para hallar la solución del cálculo de la deflexión, y es esto a lo que el presente proyecto está dedicado. El presente proyecto tratará de calcular las aproximaciones de las ecuaciones diferenciales dadas mediante la aplicacion de diferentes métodos numéricos que se van a desarrollar: è Método del disparo lineal; para ecuaciones lineales, se basa en la sustitución del problema lineal con valor de frontera por dos problemas con valor inicial. è Método del disparo para problemas no lineales; la solución a este problema no puede expresarse como una combinación lineal de las soluciones de los problemas de dos valores iniciales. Se necesitan utilizar las soluciones de una sucesión de problemas con un valor inicial. è Método de diferencias finitas para problemas lineales; se basa en reemplazar las derivadas en la ecuación diferencial mediante una aproximación de cociente de diferencias adecuada. è Método de diferencias finitas para problemas no lineales; se parece al método lineal, pero en este caso el sistema de ecuaciones no será lineal y, por lo mismo se requiere un proceso iterativo para resolverlo. Proyecto Fin de Carrera è 4 Método de Rayleigh-Ritz; en este método el problema se aborda de una forma distinta, ya que se reformula el problema de valor de frontera como un problema que consiste en seleccionar, del conjunto de todas las funciones suficientemente derivables que satisfacen las condiciones de frontera, aquélla que reduzca al mínimo una determinada integral. La motivación del presente proyecto es realizar un software sencillo e intuitivo capaz de calcular, una vez introducida la ecuación, la aproximación a dichas funciones utilizando los métodos citados anteriormente. Y así permitir el cálculo de las deflexiones de las vigas en los problemas de Ingeniería Civil, entre otras áreas técnicas. Conocer diversos algoritmos para la aproximación de ecuaciones diferenciales no estudiados durante toda la carrera es otra motivación, ya que amplían los conocimientos de matemáticas adquiridos hasta el momento y proporcionan una aplicación práctica a estas aproximaciones como puede ser en el ámbito de la Ingeniería Civil. Otra motivación es aprender la utilización de la herramienta y el lenguaje Mathematica que es un programa orientado a áreas científicas, de ingeniería, matemáticas y áreas computacionales. Software para la resolución de EDO 5 2. Objetivos del proyecto Los objetivos que se proponen para este proyecto han sido los de conocer e implementar cinco métodos diferentes para aproximar con un grado de similitud aceptable ecuaciones diferenciales procedentes, en este caso, del cálculo de las deflexiones de vigas de longitud l al aplicarle una fuerza, entre otras aplicaciones prácticas. Además, se intenta mostrar a través de una aplicación software estas aproximaciones calculadas con unas gráficas para poder observar la solución obtenida por el programa. Por lo tanto, otro objetivo que se propone es el de diseñar dicha aplicación con una interfaz de usuario que permita insertar las fórmulas y mostrar los resultados obtenidos y la función gráfica de la aproximación y de la solución exacta. Además se considera la finalidad educativa y formativa la intencionalidad principal del proyecto. A continuación, se citan los objetivos propuestos para el desarrollo correcto de la aplicación: 1.- Estudio del método del disparo lineal para su comprensión, y así diseñar un algoritmo para su posterior programación. Realización de diferentes ejercicios para comprobar el correcto funcionamiento del programa. Este método implementa para su funcionamiento el método de Runge-Kutta, con lo cual también es necesario su estudio. 2.- Estudio del método del disparo no lineal para su comprensión y el posterior Proyecto Fin de Carrera 6 diseño del algoritmo y programación del mismo. De igual manera, se requiere la programación de diferentes ejercicios para comprobar el correcto funcionamiento del programa. Aquí hay que enfrentarse a un método que trata problemas que no son lineales como en el método anterior. 3.- Estudio del método de las diferencias finitas para su comprensión, y diseñar el algoritmo y posteriormente su programación. Se realizarán diferentes ejercicios para comprobarlo. Este método trata problemas diferentes a los anteriores, ya que presentan la dificultad de que son algo inestables. 4.- Estudio del método de las diferencias finitas no lineal, diseño del algoritmo y programación. Se realizará una tanda de ejercicios para comprobar su funcionamiento. Este método trata problemas que son también algo inestables pero que además son no lineales. 5.- Estudio del método de Rayleigh-Ritz, que se compone de dos métodos: el método lineal segmentario y el método de los trazadores cúbicos. Diseño de ambos algoritmos y su programación. De igual manera hay que realizar ejercicios para su comprobación. Este es sin duda el método más complejo por su forma de tratar los problemas. 6.- Diseño y programación de una interfaz de usuario para la aplicación que permita al usuario realizar de manera cómoda el cálculo de las aproximaciones de las ecuaciones introducidas y que muestre los resultados de forma gráfica. Se realizará gracias a un paquete que se añade a Mathematica y que permite la creación de estos interfaces. Software para la resolución de EDO 7 3. Análisis de requisitos 3.1. Requisitos funcionales RF001. Métodos de la aplicación. La aplicación debe implementar sies métodos de aproximación de ecuaciones diferenciales para generar dicha aproximación y gráficos que muestren el resultado. Los métodos que se implementen serán los siguientes: Método del disparo lineal. Método del disparo no lineal. Método lineal de las diferencias finitas. Método lineal de las diferencias finitas para problemas no lineales. Método de Rayleigh-Ritz lineal segmentario. Método de Rayleigh-Ritz trazadores cúbicos. RF002. Método del disparo lineal. Resuelve de forma aproximada ecuaciones diferenciales de segundo orden, con unas condiciones de frontera y un valor inicial. Se requieren unas condiciones que garanticen la existencia de una solución para dicha función. - y≥ + pHxL y£ + qHxL y + rHxL = 0, a§x§b yHaL = a yHbL = b. (1) Proyecto Fin de Carrera 8 RF003. Método del disparo no lineal. Resuelve de forma aproximada ecuaciones diferenciales de segundo orden, con unas condiciones de frontera y un valor inicial. Se necesitan unas condiciones que garanticen la existencia de una solución para la función. y≥ = f Hx, y, y£ L, a§x§b f HaL = yHaL = a f HbL = yHbL = b. (2) RF004. Método lineal de las diferencias finitas. Resuelve de forma aproximada ecuaciones diferenciales de segundo orden, con unas condiciones de frontera y un valor inicial. Se requieren unas condiciones que garanticen la existencia de una solución para dicha función. y≥ = pHxL y£ + qHxL y + rHxL, a§x§b yHaL = a yHbL = b. (3) RF005. Método lineal de las diferencias finitas para problemas no lineales. Resuelve de forma aproximada ecuaciones diferenciales de segundo orden, con unas condiciones de frontera y un valor inicial. Se requieren unas condiciones que garanticen la existencia de una solución para dicha función. y≥ = f Hx, y, y£ L, a§x§b yHaL = a yHbL = b. (4) Software para la resolución de EDO 9 RF006. Método de Rayleigh-Ritz lineal segmentario. Resuelve de forma aproximada ecuaciones diferenciales de segundo orden, con unas condiciones de frontera y un valor inicial. Se requieren unas condiciones que garanticen la existencia de una solución para dicha función. - „ „x „y + qHxL y = f HxL, „x 0§ x § 1 y H0L = y H1L = 0. pHxL (5) RF007. Método de Rayleigh-Ritz trazadores cúbicos. Resuelve de forma aproximada ecuaciones diferenciales de segundo orden, con unas condiciones de frontera y un valor inicial. Se requieren unas condiciones que garanticen la existencia de una solución para dicha función. - „ „x „y + qHxL y = f HxL, „x 0 § x § 1, y H0L = yH1L = 0. pHxL (6) Proyecto Fin de Carrera 10 RF008. Interfaz de Usuario. El interfaz de usuario debe permitir la ejecución de todos los métodos de una forma sencilla para el usuario y que a su vez muestre los resultados de forma clara. Este interfaz debe contener las siguientes ventanas: Ventana menú. Al iniciar la aplicación aparecerá una ventana donde se podrá elegir el método que se desea ejecutar. Además debe incluir un acceso a una ayuda para el usuario. Ventana para el método del disparo lineal. Debe incluir tres casillas de texto para introducir la ecuación a aproximar, dos casillas para introducir los valores del intervalo, dos casillas para introducir los valores de frontera del intervalo y otra última casilla para introducir el tamaño del paso del intervalo. También debe mostrar la solución obtenida mostrando los puntos de la aproximación obtenida y un gráfico comparativo. Ventana para el método del disparo no lineal. Debe incluir una casilla de texto para introducir la ecuación a aproximar, dos casillas para introducir los valores del intervalo, dos casillas para introducir los valores de frontera del intervalo y otra última casilla para introducir el tamaño del paso del intervalo. Así mismo debe mostrar la solución calculada mostrando los puntos de la aproximación obtenida y un gráfico comparativo. Software para la resolución de EDO 11 Ventana para el método lineal de diferencias finitas. Debe incluir tres casillas de texto para introducir la ecuación a aproximar, dos casillas para introducir los valores del intervalo, dos casillas para introducir los valores de frontera del intervalo y otra última casilla para introducir el tamaño del paso del intervalo. Debe mostrar la solución obtenida mostrando los puntos de la aproximación obtenida y un gráfico comparativo. Ventana para el método lineal de diferencias finitas para problemas no lineales. Debe incluir una casilla de texto para introducir la ecuación a aproximar, dos casillas para introducir los valores del intervalo, dos casillas para introducir los valores de frontera del intervalo y otra última casilla para introducir el tamaño del paso del intervalo. Así mismo debe mostrar la solución obtenida mostrando los puntos de la aproximación obtenida y un gráfico comparativo. Ventana para el método de Rayleigh-Ritz lineal segmentario. Debe incluir tres casillas de texto para introducir la ecuación a aproximar, dos casillas para introducir los valores del intervalo, dos casillas para introducir los valores de frontera del intervalo y otra última casilla para introducir el número de subintervalos que se realizarán del intervalo. Así mismo debe mostrar la solución obtenida mostrando los puntos de la aproximación obtenida y un gráfico comparativo. Ventana para el método de Rayleigh-Ritz trazadores cúbicos. Debe incluir tres casillas de texto para introducir la ecuación a aproximar, dos casillas para introducir los valores del intervalo, dos casillas para introducir los valores de frontera del intervalo y otra última casilla para introducir el número de subintervalos que se realizarán del intervalo. Así Proyecto Fin de Carrera 12 mismo debe mostrar la solución obtenida mostrando los puntos de la aproximación obtenida y un gráfico comparativo. Ventana ayuda al usuario. Debe contener una ayuda para que el usuario sepa cómo debe ejecutar cada método, qué parámetros usa y su pseudocódigo. Ventana acerca de la aplicación. Debe contener los datos relevantes de la aplicación, nombre, autor, director y otros datos que se consideren. Software para la resolución de EDO 13 4. Metodología A continuación, se describe la metodología utilizada para el desarrollo de la aplicación del proyecto, la cual, al tratarse de un desarrollo de un software que implementa funciones matemáticas, no utiliza una metodología estándar. La metodología de desarrollo empleada está basada en el modelo estructurado de Yourdon y se siguen unos determinados pasos formales necesarios en este desarrollo, pero adaptándola a las necesidades de implementación del proyecto. Seguidamente se muestra de manera gráfica las diferentes fases en la que se observa que se han propuesto diferentes paquetes de trabajo (WP). Fases del desarrollo de la aplicación. Figura 4 Proyecto Fin de Carrera 14 WP.01.- Definición del problema. Es el paquete de trabajo fundamental para el desarrollo del proyecto, ya que se estudiarán todas las propuestas e ideas que se tienen para el desarrollo del mismo. Se marcan los límites y alcance del proyecto y de qué manera serán abordados. De esta manera se obtendrán los objetivos generales a conseguir. Es necesario obtener y estudiar información relacionada con los métodos de aproximación que se van a programar en el proyecto para tener todo el conocimiento necesario para el correcto desarrollo. Así como las herramientas que se van a emplear para el mismo. WP.02.- Análisis de requisitos. En este paquete de trabajo se procederá a describir y a analizar todo lo que la aplicación tiene que poder hacer una vez que el proyecto esté terminado. Se clasifican requisitos como funcionales y no funcionales, divididos a su vez en requisitos para cada uno de los métodos que se implementan. Estos requisitos han de ser tenidos en cuenta durante todo el desarrollo del proyecto y tienen que ser verificados en la fase de pruebas. Software para la resolución de EDO 15 WP.03.- Desarrollo de los métodos. Este módulo de trabajo a su vez se ha dividido en otro ciclo iterativo que se repite para cada método, de manera que cada método se termina totalmente antes de pasar al siguiente, con un mayor grado de complejidad. A continuación se puede ver de manera gráfica lo explicado anteriormente. Desarrollo de los métodos numéricos. Figura 5 WP.03.1.- Análisis de conceptos. Se estudia en profundidad el método a implementar. Es necesario buscar toda la información posible para conseguir una correcta relación de conceptos así como de todas las funciones que a su vez utiliza el método. Proyecto Fin de Carrera 16 WP.03.2.- Análisis de requisitos. Es necesario aplicar todos los requisitos específicos que se propusieron para cada uno de los métodos, como la manera de introducir las ecuaciones, cómo deben tratarse y cómo tienen que ser las salidas. WP.03.3.- Diseño del algoritmo. Es necesario escribir un pseudocódigo con toda la información recabada hasta este punto, que cumpla con los requisitos y funcionalidades necesarios. WP.03.4.- Codificación del método. Se codifica en el lenguaje especificado el pseudocódigo del paquete de trabajo anterior, de manera que pueda implementar ya la funcionalidad requerida correctamente. WP.03.5.- Realización de ejercicios de prueba. En este paquete de trabajo se tiene que probar rigurosamente el correcto funcionamiento del método implementado, de no ser así, se debe volver a la codificación del método (WP.03.5) si el fallo es de programación, o al diseño del algoritmo (WP.03.4) si el fallo es conceptual. WP.03.6.- Documentación del método. Se realiza una explicación detallada de la funcionalidad del método. Software para la resolución de EDO 17 WP.04.- Desarrollo del interfaz de usuario. Este módulo de trabajo a su vez se ha dividido en otro ciclo iterativo que se repite para cada método, de manera que cada método tiene su interfaz totalmente terminada antes de pasar al siguiente. De igual manera, como se especifica en los requisitos, se desarrolla un interfaz menú desde el que se acceden a los demás. A continuación se puede ver de manera gráfica. Desarrollo del interfaz de usuario HGUIL. Figura 6 WP.04.1.- Análisis de requisitos del interfaz. Es necesario aplicar todos los requisitos específicos que se propusieron para cada uno de los interfaces de cada método, como la manera de introducir las ecuaciones y cómo tienen que mostrarse las salidas. Proyecto Fin de Carrera 18 WP.04.2.- Diseño del interfaz. Es necesario realizar un diseño previo de cuáles serán y de cómo aparecerán los componentes del interfaz para que se adapte a los requisitos expuestos. WP.04.3.- Programación del interfaz. Se programa en el lenguaje y con la herramienta especificada de manera que se pueda ejecutar la funcionalidad completa requerida. WP.04.4.- Realización de pruebas del interfaz. Se realizan pruebas de entrada y salida. De manera que si ocurriera algún error se tendría que volver al paquete de programación del interfaz (WP.04.3) para subsanarlo si el error fuera de programación o al paquete de diseño del interfaz (WP.04.2) si el error fuera de diseño o si no se ajustase a los requisitos. WP.05.- Realización de pruebas globales. En este paquete de trabajo se comprueba la funcionalidad completa de la aplicación. Hay que validar que el programa hace lo que tiene que hacer, navegar correctamente por la aplicación, y comprobar que la ejecución es correcta y que muestra los resultados correctos en función del método elegido. Si se produce algún error se tiene que volver al método donde ha ocurrido y verificarlo de nuevo. Software para la resolución de EDO 19 También se tiene que validar el cumplimiento de todos los requisitos enunciados al comienzo del desarrollo. WP.06.- Documentacion final. En este paquete de trabajo se ha considerado que se deben desarrollar dos tareas fundamentalmente. Se puede observar gráficamente a continuación. Documentación final. Figura 7 WP.06.1.- Documentación del proyecto. Se describe con detalle todos los métodos implementados, así como todos los componentes del ciclo de desarrollo utilizados, valoración económica, planificación, además de todos los documentos que se consideren oportunos. WP.06.2.- Realización de manual de usuario. En este paquete de trabajo se realiza un documento para la ayuda al usuario al manejo de la aplicación, navegación por la misma, explicación de funcionalidad y temas que puedan resultarle de interés para una correcta utilización del software. Proyecto Fin de Carrera 20 5. El método del disparo lineal En los métodos de la serie de Taylor para resolver problemas de valor inicial el error global final es del orden de O IhN M, donde N se puede elegir suficientemente grande para que el error sea pequeño. El inconveniente de este método es la elección del valor de N y el cálculo de las derivadas, que puede ser muy complicado. Cada método de Runge-Kutta se deriva del correspondiente de Taylor de orden N en el que el error global final es del orden de O IhN M. Se realiza una simplificación para realizar varias evaluaciones de funciones en cada paso para eliminar el cálculo de las derivadas de orden superior. Estos métodos se pueden construir para cualquier orden N . 5.1. Método de Runge-Kutta El método más empleado es el de orden N = 4 ya que es muy preciso, estable y fácil de programar. El método de Runge-Kutta de orden cuarto, también llamado RK4 simula la precisión del de la serie de Taylor de orden N = 4. Se basa en el cálculo de la aproximación yi+1 del modo siguiente: yi+1 = yi + w1 F1 + w2 F2 + w3 F3 + w4 F4 , (7) siendo F1 = h F2 = h F3 = h F4 = h f Hxi , yi L, f Hxi + a1 h, yi + b1 F1 L, f Hxi + a2 h, yi + b2 F1 + b3 F2 L, f Hxi + a3 h, yi + b4 F1 + b5 F2 + b6 F3 L. (8) Software para la resolución de EDO 21 Si se igualan los coeficientes con los del método de la serie de Taylor de orden N = 4, de modo que el error local sea del orden O Ih5 M, en el método de Runge-Kutta se obtiene el siguiente sistema de ecuaciones: b1 = a1 , b2 + b3 = a2 , b4 + b5 + b6 = a3 , w1 + w2 + w3 + w4 = 1, w2 a 1 + w 3 a 2 + w 4 a 3 = 1 2 , w2 a 1 2 + w 3 a 2 2 + w 4 a 3 2 = w2 a 1 3 + w 3 a 2 3 + w 4 a 3 3 = 1 3 1 4 , , w3 a1 b3 + w4 Ha1 b5 + a2 b6 L = (9) 1 6 , w3 a1 a2 b3 + w4 a3 Ha1 b5 + a2 b6 L = w3 a1 2 b3 + w4 Ia1 2 b5 + a2 2 b6 M = w4 a 1 b 3 b 6 = 1 24 1 8 1 12 , , . El sistema tiene 11 ecuaciones y 13 incógnitas. Las dos condiciones adicionales más empleadas son a1 = 1 2 , b2 = 0. (10) Con estas restricciones la solución al sistema de ecuaciones viene dado por los valores Proyecto Fin de Carrera a1 = b1 = w1 = 1 2 1 , a2 = 22 1 2 , a3 = 1, , b2 = 0, b3 = 2 1 6 1 , w2 = 3 1 2 , w3 = , b4 = 0, b5 = 0, b6 = 1, 1 3 , w4 = 1 6 (11) . Sustituyendo estas variables en la fórmula general del método de Runge-Kutta de orden N = 4, se obtiene la siguiente regla para generar los las aproximaciones yi+1 : yi+1 = yi + HF1 + 2 F2 + 2 F3 + F4 L 6 , F1 = h f Hxi , yi L, h 1 F2 = h f xi + , yi + F1 , 2 2 h 1 F3 = h f xi + , yi + F2 , 2 2 F4 = h f Hxi + h, yi + F3 L. (12) Se llama método de cuarto orden debido a que reproduce los términos de la serie de Taylor incluyendo el término h4 , por lo que el error es O Ih5 M. Error del método frente al tamaño del paso El término de error de la regla de Simpson usada para aproximar la integral de la expresión yHx1 L - yHx0 L = Ÿ x 1 f Hx, yHxLL „ x con un tamaño de paso de h ê 2 viene dado por x 0 - y HxL H4L h5 2880 . (13) Si este fuera el único error cometido en cada paso, entonces después de los M pasos el error acumulado por el método de Runge-Kutta de orden N = 4 HRK4L sería: Software para la resolución de EDO -‚ M i=1 y Hxi L H4L h5 2880 º 23 Hb - aL 5760 yH4L HxL h4 º O Ih4 M. (14) El método de RK4 tiene un error global final de orden O Ih4 M. Precisión del método de Runge-Kutta Se supone que yHxL es la solución del problema de valor inicial e yHxL œ C 4+1 @x0 , bD, M y 8Hxi , yi L<i=0 es la sucesión de aproximaciones generadas por el método de Runge-Kutta de orden 4. Entonces: ei = †yHxi L - yi § = O Ih4 M , ei+1 = †yHxi+1 L - Hyi + h Tn Hxi , yi LL§ = O Ih4+1 M = OIh5 M, Tn Hxi , yi L = ‚ yH jL Hxi L n j! j=1 (15) h j-1 . El error global final del intervalo en el extremo derecho viene dado por EHyHbL, hL = †yHbL - yM § = O Ih4 M. (16) Si se emplea el método de Runge-Kutta de orden N = 4 con tamaños de paso h y h ê 2, se obtiene un error global final que viene dado por: EHyHbL, hL º C h4 , E yHbL, h 2 ºC h 2 4 = 1 16 C h4 º 1 16 EHyHbL, hL. (17) Si el tamaño de paso se reduce a la mitad en el método RK4 el error global final se reducirá en un factor de 1 . 16 A continuación se presenta el algoritmo que calcula los valores del problema de valor inicial empleando el método de Runge-Kutta de orden N = 4. Proyecto Fin de Carrera 24 è Algoritmo 1. Método de Runge-Kutta de orden N = 4 HRK4L Input Hy£ = f Hx, yL , yHaL = y0 , a, b, hL n ≠ Hb - aL ê h x0 ≠ a For i = 0, 1, 2, 3, ..., n - 1 do F1 ≠ h f Hxi , yi L F2 ≠ h f Jxi + 2 , yi + h F3 ≠ h f Jxi + 2 , yi + h 1 2 1 2 F1 N F2 N F4 ≠ h f Hxi + h, yi + F3 L yi+1 ≠ yi + 1 ê 6 HF1 + 2 F2 + 2 F3 + F4 L xi+1 ≠ xi + h End Return H8y0 , y1 , ..., yn <L Output 5.2. Método del disparo lineal Es el método utilizado para resolver de manera aproximada ecuaciones diferenciales de segundo orden, con unas condiciones de frontera y un valor inicial. Se proponen una serie de condiciones que garantizan la existencia de una solución para dicha función. ô Teorema 1. Se supone: y≥ = f Hx, y, y£ L, a b x b b, f HaL = a, f HbL = b continua en el conjunto D = 8Hx, y, y£ L » a § x § b, -¶ < y < ¶, -¶ < y£ < ¶< y ∑ f ê ∑ y y ∑ f ê ∑ y£ son también continuas en D. Si ∑f ∑y Hx, y, y£ L > 0 para toda Hx, y, y£ L œ D y existe una constante M , con Software para la resolución de EDO … ∑f ∑y 25 Hx, y, y£ L … § M , para toda Hx, y, y£ L œ D,entonces el problema tiene una solución única. El método del disparo se basa en dividir la función en dos funciones y1 HxL y y2 HxL que se obtienen de manera aproximada, después se aproxima la solución mediante la siguiente ecuación: yHxL = y1 HxL + b - y1 HbL y2 HbL y2 HxL. (18) Esta ecuación representa la solución única al problema con valor de frontera siempre y cuando y2 HbL ∫ 0. El algoritmo que se utiliza para obtener una aproximación a la función es el siguiente. Con la función: y≥ = pHxL y£ + qHxL y + rHxL (19) se toman como datos de entrada los extremos a y b, las condiciones de frontera a y b, yHaL = a e yHbL = b, y el número de subintervalos N . Proyecto Fin de Carrera 26 è Algoritmo 2. Método del disparo lineal Input HpHxL, qHxL, r HxL, a, b, a, b, hL matriz u, v, k, kp, w vector xi , yi (* Se inicializan los vectores y matrices *) For i = 1, ..., 4 do For j = 1, 2 do ki, j ≠ 0 kpi, j ≠ 0 End End For i = 0, ...., 60 - 1 do xi ≠ 0 End For i = 0, ..., 3 - 1 do For j = 0, ..., 60 - 1 do ui, j ≠ 0 vi, j ≠ 0 wi, j ≠ 0 End End n ≠ Round B b-a F; h u1,0 ≠ a u2,0 ≠ 0 v1,0 ≠ 0 v2,0 ≠ 1 For i = 0, 1, ..., n - 1 do xi ≠ a + i µ h k1,1 ≠ h µ u2,i k1,2 ≠ h µ IpHxi L µ u2,i + q Hxi L µ u1,i + rHxi LM k2,1 ≠ h µ Iu2,i + 1 2 k2,2 ≠ h µ Jp Jxi + µ Iu1,i + k3,1 ≠ h µ Iu2,i + 1 2 k3,2 ≠ h µ Jp Jxi + µ Iu1,i + k1,2 M h N µ Iu2,i 2 1 2 + 1 2 h k1,1 M + rJxi + 2 NN h k2,2 M h N µ Iu2,i 2 1 2 k1,2 M + q Jxi + 2 N µ + 1 2 k2,2 M + q Jxi + 2 N µ h k2,1 M + rJxi + 2 NN k4,1 ≠ h µ Iu2,i + k4,2 M h Software para la resolución de EDO 27 k4,2 ≠ h µ IpHxi + hL µ Iu2,i + k3,2 M + qHxi + hL µ Iu1,i + k3,1 M + rHxi + hLM 1 6 1 6 u1,i+1 ≠ u1,i + u2,i+1 ≠ u2,i + Ik1,1 + 2 k2,1 + 2 k3,1 + k4,1 M Ik1,2 + 2 k2,2 + 2 k3,2 + k4,2 M k £ 1,1 ≠ h µ v2,i k £ 1,2 ≠ h µ IpHxi L µ v2,i + qHxi L µ v1,i M k £ 2,1 ≠ h µ Iv2,i + k £ 2,2 ≠ h 1 £ k 1,2 M 2 h µ JpJxi + 2 N µ Iv2,i qJxi + 2 N µ Iv1,i + h k £ 3,1 ≠ h µ Iv2,i + k £ 3,2 ≠ 1 2 1 £ k 2,2 M 2 h h µ JpJxi + 2 N µ Iv2,i qJxi + 2 N µ Iv1,i + h k £ 4,1 ≠ h µ Iv2,i + k £ 3,2 M 1 2 + 1 2 k £ 1,2 M + 1 2 k £ 2,2 M + k £ 1,1 MN + k £ 2,1 MN k £ 4,2 ≠ h µ IpHxi + hL µ Iv2,i + k £ 3,2 M + qHxi + hL µ Iv1,i + k £ 3,1 MM v1,i+1 ≠ v1,i + 1 6 Ik £ 1,1 + 2 k £ 2,1 + 2 k £ 3,1 + k £ 4,1 M v2,i+1 ≠ v2,i + 1 6 Ik £ 1,2 + 2 k £ 2,2 + 2 k £ 3,2 + k £ 4,2 M End w1,0 ≠ a w2,0 ≠ b-u1,n v1,n For i = 0, 1, ..., n do w1,i = u1,i + w2,0 µ v1,i w2,i = u2,i + w2,0 µ v2,i End Return J8xi <ni=0 , 9w1,i =i=0 N n Output Proyecto Fin de Carrera 28 Ejemplo. à Problema 1. Represéntese con u el potencial electrostático entre dos esferas metálicas concéntricas de radio R1 y R2 con R1 < R2 , tales que el potencial de la esfera interior se mantenga constante en V1 voltios y el potencial de la esfera exterior sea 0 volts. El potencial de la región situada entre ambas esferas está regido por la ecuación de Laplace, que en esta aplicación particular se reduce a: „2 u „r2 + 2 „u r „r = 0 R1 b r b R2 uHR1 L = V1 , uHR2 L = 0 Supóngase que R1 = 2 plg, R2 = 4plg y que V1 = 110volts. Aproximar uH3L por medio del algoritmo del disparo lineal. Comparar los resultados de la parte (a) con el potencial real uH3L, donde a) b) uHrL = V1 R1 r I R 2-R M. R -r 2 1 Método del disparo lineal para el problema con valor de frontera: 2 y≥ = - y£ + 0y + 0 x h = 0.2 x œ @2., 4.D, yH2.L = 110., yH4.L = 0. i 0 1 2 3 4 5 6 7 8 9 10 xi 2.0000000000 2.2000000000 2.4000000000 2.6000000000 2.8000000000 3.0000000000 3.2000000000 3.4000000000 3.6000000000 3.8000000000 4.0000000000 Tabla de errores u1,i 110.0000000000 110.0000000000 110.0000000000 110.0000000000 110.0000000000 110.0000000000 110.0000000000 110.0000000000 110.0000000000 110.0000000000 110.0000000000 v1,i 0.0000000000 0.1818140590 0.3333271869 0.4615313634 0.5714210884 0.6666591047 0.7499925253 0.8235221130 0.8888818110 0.9473615838 0.9999934088 w1,i 110.0000000000 90.0003216920 73.3337677598 59.2312153917 47.1432659743 36.6670151264 27.5002784455 19.4119704861 12.2223563183 5.7895389053 0.0000000000 w2,i -110.0007250420 -90.9098962614 -76.3896741012 -65.0894867210 -56.1231128776 -48.8894884031 -42.9692901652 -38.0627707556 -33.9510573337 -30.4713128917 -27.5003625208 Software para la resolución de EDO xi w1,i 29 yHxi L »w1,i - yHxi L» 2.0000000000 110.0000000000 110.0000000000 2.2000000000 90.0003216920 90.0000000000 2.4000000000 73.3337677598 73.3333333333 0.0000000000 0.0003216920 0.0004344264 2.6000000000 59.2312153917 59.2307692308 0.0004461609 2.8000000000 47.1432659743 47.1428571429 0.0004088314 3.0000000000 36.6670151264 36.6666666667 0.0003484598 3.2000000000 27.5002784455 27.5000000000 0.0002784455 3.4000000000 19.4119704861 19.4117647059 0.0002057803 3.6000000000 12.2223563183 12.2222222222 0.0001340961 5.7894736842 0.0000000000 0.0000652211 0.0000000000 3.8000000000 4.0000000000 5.7895389053 0.0000000000 Gráficas de la solución de la ecuación diferencial 110 H4 - xL yHxL = x y la aproximación obtenida con el método del disparo lineal con un tamaño de paso h = 0.2 Y 100 80 60 40 20 2.5 3.0 3.5 4.0 X Proyecto Fin de Carrera 30 6. El método del disparo no lineal Este método se utiliza para resolver problemas no lineales con valor de frontera de segundo orden: y≥ = f Hx, y, y£ L, a § x § b, f HaL = yHaL = a, f HbL = yHbL = b. (20) Tiene parecido con el método anterior sin embargo la solución de un problema no lineal no puede expresarse como una combinación de dos problemas iniciales, así que para este método se utiliza en lugar de dos problemas una sucesión de ellos, donde t es un parámetro para la aproximación de la solución, de la siguiente forma: y≥ = f Hx, y, y£ L, a § x § b, yHaL = a, y£ HaL = t. (21) Se escoge el parámetro t = tk de tal forma que lím yHb, tk L = yHbL = b, kz¶ donde yHb, tk L es la solucion del problema de valor inicial con t = tk e yHxL es la solución al problema con valor de frontera. La ténica que se sigue es empezar con un parámetro t0 , que determinará la posición inicial a partir de la cual se traza una recta que tratará de aproximar la solución, como si de un disparo se tratase, buscando el objetivo desde el punto Ha, aL a lo largo de la curva que describe la solución al problema de valor inicial dado por y≥ = f Hx, y, y£ L, a § x § b, yHaL = a, y£ HaL = t0 . Software para la resolución de EDO 31 y β • y (b, t 0) (b, y (b, t0)) y (x, t0) pendiente t 0 • α (a, α ) x b a Problema del valor inicial con la elevación inicial t0 desde el punto Ha, aL. Figura 8 Si yHb, t0 L no está lo suficientemente cerca de b se utilizarán las elevaciones t1 , t2 , ... y así sucesivamenete hasta que se considere que el valor yHb, tk L se aproxima lo suficiente al valor b, es decir, se acierte en el blanco. Véase la siguiente figura. y y (b, t 2) • y (x, t2) β y (b, t 3) • y (x, t3) y (b, t1) • y (x, t1) y (b, t 0) • y (x, t0) α (a, α ) • a Problema del valor inicial con diferentes elevaciones. Figura 9 b x Proyecto Fin de Carrera 32 Los parámetros tk se calculan de tal forma que: yHb, tL - b = 0. Ecuación no lineal en cuya resolución se puede aplicar el método de Newton o del de la Secante. Para utilizar el método de la Secante se necesitan unas aproximaciones iniciales t0 y t1 y luego generar las t restantes mediante la siguiente ecuación: tk = tk-1 - HyHb, tk-1 L - bL Htk-1 - tk-2 L yHb, tk-1 L - yHb, tk-2 L , k = 2, 3, ... (22) Para generar la misma sucesión 8tk < con el método de Newton sólo se necesita la primera aproximación de la sucesion t0 . Se aplica la siguiente ecuación: tk = tk-1 - yHb, tk-1 L - b „y „t Hb, tk-1 L . Este método requiere que se conozca (23) „y „t Hb, tk-1 L, que es un problema porque no se dispone de la función yHb, tL, sólo de unos valores yHb, t0 L, yHb, t1 L, ... , yHb, tk-1 L. Si se modifica el problema de valor inicial (20), teniendo en cuenta que la solución se basa en y y en t se tiene: y≥ Hx, yL = f Hx, yHx, tL, y£ Hx, tLL, a § x § b, yHa, tL = a, y Ha, tL = t. £ (24) Software para la resolución de EDO Para calcular „y „t 33 Hb, tL cuando t = tk-1 , se calcula la derivada parcial de la ecuación anterior respecto de t: ∑ y≥ ∑t ∑ y≥ ∑t Hx, tL = Hx, tL = ∑ f ∑t ∑ f Hx, yHx, tL, y£ Hx, tLL Hx, yHx, tL, y£ Hx, tLL ∑x (25) ∑t ∑f ∑y ∑ f ∑ y£ + Hx, yHx, tL, y£ Hx, tLL + £ Hx, yHx, tL, y£ Hx, tLL . ∑y ∑t ∑ y ∑t ∑x Dado que x y t son independientes entonces ∑ y≥ ∑t ∑f ∑y ∑x ∑t =0y Hx, tL = Hx, yHx, tL, y£ Hx, tLL ∑y ∑t Hx, tL + ∑f ∑ y£ Hx, yHx, tL, y£ Hx, tLL ∑ y£ ∑t (26) . con a § x § b. Las condiciones iniciales resultan: ∑y ∑t Ha, tL = 0 ∑ y£ ∑t y Ha, tL = 1. Si se simplifica la ecuación anterior usando zHx, tL en lugar de ∑y ∑t Hx, tL y si se invierte el orden de derivar de x y de t, se convierte en el problema de valor inicial: z≥ Hx, tL = ∑f ∑y Hx, y, y£ L zHx, tL + ∑f ∑ y£ Hx, y, y£ L z£ Hx, tL, a § x § b, zHa, tL = 0, z£ Ha, tL = 1, zHx, tL = ∑y ∑t Hx, tL. (27) Como se ve, el método de Newton necesita que los dos problemas de valor inicial sean resueltos en cada iteración del método. Proyecto Fin de Carrera tk = tk-1 - 34 yHb, tk-1 L - b zHb, tk-1 L . (28) De todos modos ningún problema de valor inicial puede resolverse de manera exacta. Se puede buscar una solución aproximada utilizando un método como éste, cuyo algoritmo se plantea un poco más abajo (algoritmo 3). En dicho algoritmo se utiliza el método de Runge-Kutta de cuarto orden para aproximar la dos soluciones que necesita el método de Newton. è Algoritmo 3. Método del disparo no lineal El siguiente algoritmo aproxima la solución numérica del problema no lineal de valor de la frontera dado por y≥ = f Hx, y, y£ L, a § x § b, f HaL = yHaL = a, f HbL = yHbL = b con un paso dado por h con una tolerancia tol o un número máximo de m iteraciones. Input H f HxL, a, b, a, b, h, tol, mL matriz k, kp, w vector xi , yi ,ui , vi (* Se inicializan los vectores y matrices *) For i = 1, ..., 4 do For j = 1, 2 do ki, j ≠ 0 kpi, j ≠ 0 End End For i = 0, ...., 60 - 1 do xi ≠ 0 End For j = 0, ..., 60 - 1 do Software para la resolución de EDO 35 ui, j ≠ 0 vi, j ≠ 0 wi, j ≠ 0 End n ≠ Round B b-a F; h a- b tk ≠ Round B b-a F; cont = 1; While cont § m do w1,0 ≠ a w2,0 ≠ tk u1 ≠ 0 u2 ≠ 1 For i = 1, 2, ..., n - 1 do xi ≠ a + Hi - 1L µ h k1,1 ≠ h µ u2,i-1 k1,2 ≠ h µ If Hxi L, w1,i-1 , ww,i-1 M k2,1 ≠ h µ Iw2,i + k2,2 ≠ h µ Jf 1 k M 2 1,2 h Hxi L + 2 , w1,i-1 + 1 2 µ k1,1 , k2,2 ≠ h µ Jf Hxi L + 2 , w1,i-1 + 1 2 µ k2,1 , 1 2 µ k3,1 , w2,i-1 + 1 2 µ k1,2 N k3,1 ≠ h µ Iuw2,i-1 + 1 2 k2,2 M h w2,i-1 + 1 2 µ k2,2 N k4,1 ≠ h µ Iw2,i-1 + k4,2 M k2,2 ≠ h µ Jf Hxi L + 2 , w1,i-1 + h w2,i-1 + w1,i+1 ≠ w1,i + w2,i+1 ≠ w2,i + 1 2 1 6 1 6 µ k3,2 N Ik1,1 + 2 k2,1 + 2 k3,1 + k4,1 M Ik1,2 + 2 k2,2 + 2 k3,2 + k4,2 M k £ 1,1 ≠ h µ v2 k £ 1,2 ≠ h µ If y Ixi , w1,i-1 , 22,i-1 M u1 + f y£ Ixi , w1,i-1 , 22,i-1 M u2 M k £ 2,1 ≠ h µ Iv2 + 1 2 k £ 1,2 M k £ 2,2 ≠ h µ If y Ixi + 2 , w1,i-1 , 22,i-1 M Iu1 + 1 + f y£ Ixi + 2 , w1,i-1 , 22,i-1 M Iu2 + 1 k £ 3,1 ≠ h µ Iv2 + 1 2 k £ 2,2 M k £ 3,2 ≠ h µ If y Ixi + 2 , w1,i-1 , 22,i-1 M Iu1 + 1 + f y£ Ixi + 2 , w1,i-1 , 22,i-1 M Iu2 + 1 1 2 µ k £ 2,2 MM 1 2 1 2 1 2 µ k £ 2,1 M µ k £ 1,1 M µ k £ 1,2 MM Proyecto Fin de Carrera 36 k £ 4,1 ≠ h µ Iv2 + k £ 3,2 M k £ 4,2 ≠ h µ If y Ixi + 2 , w1,i-1 , 22,i-1 M Iu1 + k £ 2,1 M 1 + f y£ Ixi + 2 , w1,i-1 , 22,i-1 M Iu2 + k £ 2,2 MM 1 v1,i+1 ≠ v1,i + 1 6 Ik £ 1,1 + 2 k £ 2,1 + 2 k £ 3,1 + k £ 4,1 M v2,i+1 ≠ v2,i + 1 6 Ik £ 1,2 + 2 k £ 2,2 + 2 k £ 3,2 + k £ 4,2 M End If … w1,N - b … b tol do For i = 0, 1, ..., N do xi ≠ a + i µ h SALIDA Ixi , w1,i , w2,i M Proceso terminado End End If tk = tk - w1,N - b u1 cont = cont + 1 End While SALIDA HNúmero máximo de iteraciones excedidoL Proceso terminado sin éxito Return J8xi <ni=0 , 9w1,i =i=0 N n Output Ejemplo. à Problema 2. La ecuación de Van der Pol: y≥ - mIy2 - 1M y£ + y = 0 rige el flujo de la corriente en un tubo al vacío con tres elementos internos. Sea m = 12 , yH0L = 0, y yH2L = 1. Aproximar la solución yHtL para t = 0.2 i, donde 1 § i § 9. Método del disparo no lineal para el problema con valor de frontera: 1 y≥ = Iy2 - 1M z - y 2 x œ @0., 2.D, yH0.L = 0., yH2.L = 1. h = 0.2 Software para la resolución de EDO i xi 37 w1,i w2,i 0 0.0000000000 0.0000000000 1.4493098115 1 0.2000000000 0.2741820867 1.2876947955 2 0.4000000000 0.5138861327 1.1076209444 3 0.6000000000 0.7168357586 0.9212303115 4 0.8000000000 0.8821406042 0.7310688000 5 1.0000000000 1.0088521172 0.5346865325 6 1.2000000000 1.0953383832 0.3282347528 7 1.4000000000 1.1393133677 0.1095119683 8 1.6000000000 1.1384586255 -0.1191497223 9 1.8000000000 1.0915768064 -0.3486231536 10 2.0000000000 1.0000169321 -0.5628194818 Gráficas de la solución de la ecuación diferencial yHxL = 88yHxL Ø InterpolatingFunction@H 0. 2. L, <>D@xD<< y la aproximación obtenida con el método del disparo lineal con un tamaño de paso h = 0.2 Y 1.0 0.8 0.6 0.4 0.2 0.5 1.0 1.5 2.0 X Proyecto Fin de Carrera 38 7. El método lineal de diferencias finitas El método de las diferencias finitas se utiliza para resolver problemas que presentan cierta inestabilidad y que con los métodos anteriormente estudiadoss no podían resolverse. Este método tiene mejor estabilidad pero cuesta más llegar a una solución con precisión. Este método sustituye las derivadas en la ecuacion diferencial mediante una aproximacion del cociente de diferencias adecuada. El problema de valor de frontera de segundo orden y≥ = pHxL y£ + qHxL y + rHxL, a § x § b, yHaL = a, yHbL = b (29) requiere utilizar las aproximaciones del cociente de diferencias para aproximar tanto a y£ como a y≥ . Primero, se escoge el número de subintervalos n + 1 en los que se va a dividir el intervalo @a, bD, cuyos extremos de estos subintervalos son los puntos de malla. Se calcula el valor del subintervalo h = Hb-aL , Hn+1L y al calcularse h así se facilita la aplicación de un algoritmo matricial con el cual se resuelve un sistema lineal que contenga una matriz n µ n. Para los puntos de malla xi , para i = 1, 2, 3, ..., n, la ecuación que se aproxima es: y≥ Hxi L = pHxi L y£ Hxi L + qHxi L yHxi L + rHxi L. (30) Al desarrollar y en el tercer polinomio de Taylor alrededor de xi evaluada en xi+1 y xi-1 , se tiene: yHxi+1 L = yHxi + hL = yHxi L + h y£ Hxi L + h2 2 y≥ Hxi L + h3 6 yH3L Hxi L + h4 24 yH4L Ixi+ M Software para la resolución de EDO 39 para alguna xi+ en Hxi , xi+1 L, y yHxi-1 L = yHxi - hL = yHxi L - h y£ Hxi L + h2 2 y≥ Hxi L - h3 6 yH3L Hxi L + h4 24 yH4L Hxi- L para alguna xi+ en Hxi , xi+1 L, suponiendo y œ C 4 @xi-1 , xi+1 D. Si se suman estas escuaciones y se simplifica se obtiene la fórmula de las diferencias centradas para y≥ Hxi L: y≥ Hxi L = 1 h2 @yHxi+1 L - 2 yHxi L + yHxi-1 LD - h2 12 yH4L Hxi L. (31) De manera semejante se obtiene para y£ Hxi L: y£ Hxi L = 1 @yHxi+1 L - yHxi-1 LD - 2h hi œ Hxi-1 , xi+1 L. h2 6 yH3L Hhi L, (32) Si se sustituyen las ecuaciones de las diferencias centradas en los términos y de la ecuación (24) resulta: yHxi+1 L - 2 yHxi L + yHxi-1 L h2 qHxi L yHxi L + rHxi L - h2 12 = pHxi LB yHxi+1 L - yHxi-1 L 2h F+ A2 pHxi L yH3L Hhi L - yH4L Hzi LE. (33) El método de diferencia finitas se obtiene utilizando esta ecuación junto con las condiciones de frontera yHaL = a e yHbL = b para definir w0 = a, wn+1 = b 2 wi - wi+1 - wi-1 h2 i = 1, 2, ..., n. + pHxi L K wi+1 - wi-1 2h O qHxi L wi = rHxi L (34) Proyecto Fin de Carrera 40 Esta ecuación se puede reescribir como sigue: - 1+ pHxi L wi-1 + I2 + h2 qHxi LM wi - 1 - h 2 h 2 pHxi L wi-1 = -h2 rHxi L. (35) Y el sistema de ecuaciones que resulta se expresa en forma de matriz tridiagonal n µ n de la forma Aw = b (36) siendo 2 + h2 qHx1 L -1 + -1 A= h 2 pHx1 L 0 h 2 pHx2 L 2 + h2 qHx2 L -1 + h 2 0 ∏ ∏ ª ∏ ∏ 0 ∫ 0 w1 w2 ª , w= wn-1 wn b= 0 ∏ ª pHx2 L ∏ 0 ∏ -1 + -h2 rHx1 L + I1 + y ∫ h 2 h 2 -h2 rHx2 L ª -1 + pHxn L h 2 pHxn-1 L 2 + h2 qHxn L pHx1 LM w0 -h2 rHxn-1 L -h2 rHxn L + I1 + h 2 pHxn LM wn+1 Se expresa en el teorema siguiente las condiciones bajo las que el sistema lineal tridiagonal anterior tiene solución única. ô Teorema 2. Se supone que p, q y r son continuas en el intervalo @a, bD. Si qHxL ¥ 0 en @a, bD, entonces el sistema lineal tridiagonal tiene una solución única siempre y cuando h < 2 L, donde L = máxa§x§b » pHxL ». Software para la resolución de EDO 41 è Algoritmo 4. Método lineal de las diferencias finitas Input HpHxL, qHxL, r HxL, a, b, a, b, hL vector xi , ai , bi , ci , di , li , ui , wi , zi (* Se inicializan vectores y matrices *) For i = 0, ...., n + 1 do xi ≠ 0 ai ≠ 0 bi ≠ 0 ci ≠ 0 di ≠ 0 li ≠ 0 ui ≠ 0 wi ≠ 0 zi ≠ 0 End n ≠ Round B b-a F-1 h x1 ≠ a + h a1 ≠ 2 + h 2 qHxi L b1 ≠ -1 + J 2 N pHxi L h d1 ≠ -h 2 rHxi L + J1 + J 2 N pHxi LN a h For i = 2, ..., n - 1 do xi ≠ a + i h ai ≠ 2 + h 2 qHxi L bi ≠ -1 + J 2 N pHxi L h ci ≠ -1 - J 2 N pHxi L h di ≠ -h 2 rHxi L End xn ≠ b - h xn+1 ≠ b an ≠ 2 + h 2 qHxn L cn ≠ -1 - J 2 N pHxn L h dn ≠ -h 2 rHxn L + J1 - J 2 N pHxn LN b h (* Se resuelve un sistema lineal tridiagonal *) l1 ≠ a1 u1 ≠ b1 a1 z1 ≠ d1 l1 For i = 2, ..., n - 1 do Proyecto Fin de Carrera 42 li ≠ ai - ci ui-1 ui ≠ bi li zi ≠ di -ci zi-1 li End ln ≠ an - cn un-1 zn ≠ dn -cn zn-1 ln w0 ≠ a wn+1 ≠ b wn ≠ zn For i = n - 1, ..., 1 do wi ≠ zi - ui wi+1 End Return I8xi <ni=0 , 8wi <ni=0 M Output Ejemplo: à Problema 3. La deflexión de una placa rectangular larga y uniformemente cargada, y que se encuentra bajo una fuerza de tensión axial, se rige por la ecuación diferencial de segundo orden. Sea S la fuerza axial y q la intensidad de la carga uniforme. La deflexión W a lo largo de la longitud elemental está dada por: W ≥ HxL = S EI WHxL + q x 2EI Hx - lL x œ @0, lD WH0L = 0, WHlL = 0. Donde l es la longitud de la placa, q la intensidad de la carga uniforme, E el módulo de elasticidad, S el esfuerzo en los extremos y el momento decentral de inercia es I . Sean l = 120 plg, q = 100 lb ê pie, E = 3.0 µ 107 lb ë plg2 , S = 1000 lb, e I = 625 plg4 . Aproximar la deflexión W HxL de la vifa en intervalos de 6 plg. Método de las diferencias finitas para el problema con valor de frontera: y≥ = 0.y£ + 5.33333µ 10-8 y + 2.66667µ 10-9 Hx - 120.L x x œ @0., 120.D, yH0.L = 0., yH120.L = 0. h = 6. Software para la resolución de EDO i 0 1 2 xi 0.0000000000 6.0000000000 12.0000000000 wi 0.0000000000 0.0022980631 0.0045304665 3 18.0000000000 0.0066384627 4 24.0000000000 0.0085702157 5 30.0000000000 0.0102808010 6 36.0000000000 0.0117322061 7 42.0000000000 0.0128933298 8 48.0000000000 0.0137399822 9 54.0000000000 0.0142548850 10 60.0000000000 0.0144276711 11 66.0000000000 0.0142548850 12 72.0000000000 0.0137399822 13 78.0000000000 0.0128933298 14 84.0000000000 0.0117322061 15 90.0000000000 0.0102808010 16 96.0000000000 0.0085702157 17 102.0000000000 0.0066384627 18 19 20 108.0000000000 114.0000000000 120.0000000000 0.0045304665 0.0022980631 0.0000000000 Gráfica de la aproximacion obtenida con el método lineal de diferencia finitas con un tamaño de paso h = 6. 43 Proyecto Fin de Carrera 44 Y 0.014 0.012 0.010 0.008 0.006 0.004 0.002 20 40 60 80 100 120 X Software para la resolución de EDO 45 8. El método lineal de diferencias finitas para problemas no lineales Este método es parecido al expuesto anteriormente para problemas lineales, sin embargo estos problemas no tendrán un sistema de ecuaciones lineal y por lo tanto hace falta un proceso iterativo para resolverlos. Sea el caso de los problemas no lineales con valor de frontera: y≥ = f Hx, y, y£ L, a § x § b, yHaL = a, yHbL = b (37) Para el desarrollo de este método se supondrá que f satisface las siguientes condiciones: ô 1.- f y las derivadas parciales f y ª ∑ f ê ∑ y y f y£ ª ∑ f ê ∑ y£ son continuas en D = 8Hx, y, y£ L » a § x § b, -¶ < y < ¶, -¶ < y£ < ¶<; 2.- f y Hx, y, y£ L ¥ d en D para alguna d > 0; 3.- Existen las constantes k y L, con k= máx Hx,y,y£ L e D f y Hx, y, y£ L , L= máx Hx,y,y£ L e D f y£ Hx, y, y£ L . Esto garantiza que exista una solución única. Al igual que en el método anterior, se divide el intervalo @a, bD en N + 1 subintervalos de ancho el valor h que se calcula como h = Hb - aL ê HN + 1L cuyos extremos se encuentran en xi = a + h i, para i = 0, 1, ... , N + 1. Si se supone que la solución exacta Proyecto Fin de Carrera 46 tiene una cuarta derivada acotada permite reemplazar y≥ Hxi L y y£ Hxi L en cada una de las ecuaciones: y≥ Hxi L = f Hxi , yHxi L, y£ Hxi LL (38) por la fórmula adecuada de diferencias centradas. Esto da, para toda i = 1, 2, ..., N , yHxi+1 L - 2 yHxi L + yHxi-1 L h2 = f xi , yHxi+1 L - yHxi-1 L 2h - h2 6 y Hhi L + H3L h2 12 y Hxi L, H4L (39) para alguna hi y zi en el intervalo Hxi-1 , xi+1 L. Los resultados del método de diferencias finitas se emplean cuando se eliminan los términos de error y las condiciones de frontera: w0 = a, wn+1 = b, y - wi+1 - 2 wi + wi-1 h2 + f Ixi , wi , para toda i = 1, 2, ..., N . wi+1 -wi-1 M 2h = 0, Software para la resolución de EDO 47 El sistema no lineal N µ N obtenido con este método es el siguiente: 2 w1 - w2 + h2 f Kx1 , w1 , w2 - a 2h O=0 w3 - w1 -w1 + 2 w2 - w3 + h2 f Kx2 , w2, 2h O=0 ª (40) -w N -2 + 2 w N -1 - w N + h2 f KxN -1 , w N -1 , -w N -1 + 2 w N + h2 f xN , w N , b - w N -1 2h w N - w N -2 2h O=0 -b=0 Este sistema tiene una solución única siempre y cuado h < 2 ê L. Para resolver este sistema con una solución aproximada, se aplica el método de Newton para sistemas no lineales. Se genera una sucesión de iteraciones HkL HkL :IwHkL 1 , w2 , ..., w N M > que converge a la solución del sistema (34), con la condición de que t H0L H0L la aproximación inicial IwH0L 1 , w2 , ..., w N M se acerque lo suficiente a la solución t Hw1, w2, ..., w N Lt , y de que la matriz jacobiana del sistema no sea singular. En el caso del sistema (34), la matriz jacobiana J Hw1, w2, ..., w N L es tridiagonal. Su elemento i j - ésimo viene dada por la expresión: J Hw1, w2, ..., w N Li, j = wi+1 -wi-1 M, 2h w -w 2 + h2 f y Ixi , wi , i+12 h i-1 M, w -w -1 - h2 f y£ Ixi , wi , i+12 h i-1 M, -1 + : h 2 f y£ Ixi , wi , i = j - 1, j = 2, ..., N i = j, j = 1, ..., N i = j + 1, j = 1, ..., N - 1 (41) Proyecto Fin de Carrera 48 donde w0 = a y w N +1 = b. El método de Newton para los sistemas no lineales requiere que en cada iteración se resuelva el sistema lineal de N µ N : J Hw1, w2, ..., w N L Hv1 , ..., vn LT = - 2 w1 - w2 - a + h2 f Kx1 , w1 , -w1 + 2 w2 - w3 + h2 f Kx2 , w2 , w3 - w1 2h O, -wN -2 + 2 w N -1 - w N + h2 f KxN -1, w N -1 , 2 -wN -1 + 2 w N + h f xN , w N , b - w N -1 2h w2 - a 2h ... , wN - w N -2 O, 2h O, (42) T -b para v1, v2 , ..., vN , porque Hk-1L wHkL + vi , para cada i = 1, 2, ..., N , i = wi Puesto que J es tridiagonal, se puede aplicar el algoritmo de factorización de Crout para los sistemas tridiagonales. El algoritmo de este método se describe a continuación. Software para la resolución de EDO 49 è Algoritmo 5. Método lineal de las diferencias finitas para problemas no lineales Input H f HxL, a, b, a, b, h, tol, mL vector xi , ai , bi , ci , di , li , ui , wi , zi (* Se inicializan vectores y matrices *) For i = 0, ...., n + 1 do xi ≠ 0 ai ≠ 0 bi ≠ 0 ci ≠ 0 di ≠ 0 li ≠ 0 ui ≠ 0 wi ≠ 0 zi ≠ 0 End n ≠ Round B b-a F-1 h w0 ≠ a wn+1 ≠ b For i = 1, ..., n do wi ≠ a + i J b-a N h b-a End cont≠1 While cont § m do x1 ≠ a + h t= Iw2 -aM 2h a1 ≠ 2 + h 2 f y Hx1 , w1 , tL b1 ≠ -1 + J 2 N f y£ Hx1 , w1 , tL h d1 ≠ -I2 w1 - w2 - a + h 2 f Hx1 , w1 , tLM For i = 2, ..., n - 1 do xi ≠ a + i h t= Hwi+1 -wi-1 L 2h 2 ai ≠ 2 + h f y Hxi , wi , tL bi ≠ -1 + J 2 N f y£ Hxi , wi , tL h ci ≠ -1 - J 2 N f y£ Hxi , wi , tL h di ≠ -I2 wi - wi+1 - wi-1 + h 2 f Hxi , wi , tLM End Proyecto Fin de Carrera 50 xn ≠ b - h t= H b-wn-1 L 2h an ≠ 2 + h 2 f y Hxn , wn , tL cn ≠ -1 - J 2 N f y£ Hxn , wn , tL h dn ≠ -I2 wn - wn-1 - b + h 2 f Hxn , wn , tLM (* Se resuelve un sistema lineal tridiagonal *) l1 ≠ a1 u1 ≠ b1 a1 z1 ≠ d1 l1 For i = 2, ..., n - 1 do li ≠ ai - ci ui-1 ui ≠ bi li zi ≠ di -ci zi-1 li End ln ≠ an - cn un-1 zn ≠ dn -cn zn-1 ln vn ≠ zn wn ≠ wn + vn For i = n - 1, ..., 1 do vi ≠ zi - ui vi+1 wi ≠ wi + vi End If »» v »» b tol do For i = 0, ..., N - 1 do xi ≠ a + i h SALIDA Hxi , wi L Proceso terminado End End If cont≠cont+1 SALIDA H ' Número de iteraciones excedido'L -1 N -1 Return I8xi <N i=0 , 8wi <i=0 M Output Software para la resolución de EDO 51 Ejemplo. à Problema 4. Sea el problema de valor de frontera y = Jx Hy£ L - 9 y2 + 4 x6 N í x5 , ≥ x œ @1, 2D, 2 2 yH1L = 0, yH2L = ln 256. y su solución exacta yHxL = x3 ln x. Aproximar la solución aplicando el método no lineal de diferencias finitas tomando h = 0.05 y una tolerancia de 10-4 . Método del diferencias finitas para el problema no lineal con valor de frontera. ≥ y = 4 x 6 + z 2 x 2 - 9 y2 x5 x œ @1., 2.D, yH1.L = 0., i 0 yH2.L = 5.54518 xi wi 1.0000000000 0.0000000000 1 2 3 1.0500000000 1.1000000000 1.1500000000 0.0562377725 0.1263684409 0.2118227193 4 1.2000000000 0.3140662227 5 1.2500000000 0.4345979113 6 1.3000000000 0.5749486970 7 1.3500000000 0.7366801826 8 1.4000000000 0.9213835170 9 1.4500000000 1.1306783480 10 1.5000000000 1.3662118644 11 1.5500000000 1.6296579151 12 1.6000000000 1.9227161994 13 1.6500000000 2.2471115203 14 1.7000000000 2.6045930975 15 1.7500000000 2.9969339343 16 1.8000000000 3.4259302347 17 1.8500000000 3.8934008681 18 1.9000000000 4.4011868793 19 1.9500000000 4.9511510405 20 2.0000000000 5.5451774445 Tabla de errores. h = 0.05 Proyecto Fin de Carrera xi 52 wi yHxi L »wi - yHxi L» 1.0000000000 0.0000000000 0.0000000000 0. 1.0500000000 0.0562377725 0.0564807138 2.4294129214µ 10-4 1.1000000000 0.1263684409 0.1268578493 4.8940844341µ 10-4 1.1500000000 0.2118227193 0.2125604441 7.3772477638µ 10-4 1.2000000000 0.3140662227 0.3150516501 9.8542746209µ 10-4 1.2500000000 0.4345979113 0.4358272487 1.2293373602µ 10-3 1.3000000000 0.5749486970 0.5764142890 1.4655920832µ 10-3 1.3500000000 0.7366801826 0.7383698367 1.6896540091µ 10-3 1.4000000000 0.9213835170 0.9232798173 1.8963003043µ 10-3 1.4500000000 1.1306783480 1.1327579472 2.0795992538µ 10-3 1.5000000000 1.3662118644 1.3684447399 2.2328755092µ 10-3 1.5500000000 1.6296579151 1.6320065809 2.3486658077µ 10-3 1.6000000000 1.9227161994 1.9251348654 2.4186660246µ 10-3 1.6500000000 2.2471115203 2.2495451902 2.4336699615µ 10-3 1.7000000000 2.6045930975 2.6069765975 2.3834999521µ 10-3 1.7500000000 2.9969339343 2.9991908635 2.2569291292µ 10-3 1.8000000000 3.4259302347 3.4279718297 2.0415950205µ 10-3 1.8500000000 3.8934008681 3.8951247721 1.7239039938µ 10-3 1.9000000000 4.4011868793 4.4024758053 1.2889259445µ 10-3 1.9500000000 2.0000000000 4.9511510405 5.5451774445 4.9518713190 7.2027851232µ 10-4 5.5451774445 0. Gráficas de la solución de la ecuación diferencial yHxL = x 3 logHxL y la aproximación obtenida con el método de las diferencias finitas no lineal con un tamaño de paso h = 0.05 Software para la resolución de EDO 53 Y 5 4 3 2 1 1.2 1.4 1.6 1.8 2.0 X Proyecto Fin de Carrera 54 9. El método de Rayleigh-Ritz Este método aborda el problema de hallar la aproximación de la función con un planteamiento distindo al visto en los anteriores métodos. Para empezar, se reformula el problema de valor de frontera como un problema que consista en seleccionar la función que reduzca al mínimo una determinada integral de entre todas las funciones suficientemente derivables que satisfagan las condiciones de frontera. El tamaño de del conjunto de funciones se disminuye, obteniéndose así una aproximación a la solución al problema de minimización y por lo tanto, una aproximación a la solución del problema con valor de frontera. 9.1. Método lineal segmentario de Rayleigh-Ritz Para explicar este método se considera la aproximación de una solución a este problema lineal con valor de frontera. Esta ecuación describe la deflexión y HxL de una viga de longitud l , con una sección transversal variable qHxL, y los exfuerzos agregados pHxL y f HxL. Satisface la la ecuación diferencial: - „ „x pHxL „y „x + qHxL y = f HxL, para 0 § x § 1 (43) con las condiciones de frontera y H0L = y H1L = 0 ô Se supone que p œ C1 @0, 1D, que q, f œ C@0, 1D y d > 0, tal que pHxL ¥ d tal que qHxL ¥ 0 para cada x en @0, 1D. (44) Software para la resolución de EDO 55 Con estas suposiciones se garantiza que el problema de valor de frontera, anteriormente descrito tiene una solución única. Los problemas con valor de frontera describen fenómenos físicos, en este caso la solución a la ecuación la viga satisface la propiedad variacional, que resulta indispensable para el desarrollo del método de Rayleigh-Ritz y que además caracteriza la solución de esa ecuación como la función que reduce al mínimo cierta integral sobre las funciones en C02 @0, 1D, el conjunto de esas funciones u en C2 @0, 1D con la propiedad de que uH0L = uH1L = 0. La caracterización de este método se establece en el siguiente teorema. ô Teorema 5. Sea p œ C1 @0, 1D, q, f œ C@0, 1D y además pHxL ¥ d > 0 qHxL ¥ 0 para 0 § x § 1. La función y œ C02 @0, 1D es la solucion única de la ecuacion diferencial „ - „x I pHxL „y M „x + qHxL y = f HxL, 0 § x § 1 si y sólo si y es la función única en C20 @0, 1D que reduce al mínimo la integral I@uD = Ÿ0 9 pHxL @u£ HxLD2 + qHxL @uHxLD2 - 2 f HxL uHxL= „ x. 1 Reduciendo al mínimo la integral, el método de Rayleigh-Ritz aproxima la solución de yHxL sólo sobre el conjunto más pequeño de las funciones que contienen combinaciones Proyecto Fin de Carrera 56 lineales de ciertas funciones básicas f1 , f2 , ..., fn . Estas funciones son linealmente independientes y satisfacen: fi H0L = fi H1L = 0, para cada i = 1, 2, ..., n. Después de resolver las constantes c1 , c2, ..., cn , que reducen al mínimo IA⁄ ni=1 ci fi E, se obtiene una aproximación fHxL = ⁄ni ci fi HxL a la solución yHxL de la ecuacion anterior. De acuerdo con la ecuación de la integral I@uD, se tiene: n I@fD = I B‚ ci fi F i=1 I@fD = (45) 2 n 1 n 2 n ‡ : pHxLB‚ ci fi HxLF + qHxLB‚ ci fi HxLF - 2 f HxL ‚ ci fi HxL> „ x £ 0 i=1 i=1 i=1 Cuando se considera I como una función de c1 , c2, ..., cn para encontrar un mínimo es necesario tener ∑I ∑ cj =0 j = 1, 2, ..., n (46) Derivando se obtiene: ∑I ∑ cj 1 n n i=1 i=1 = ‡ :2 pHxL ‚ ci f£ i HxL f£ j HxL + 2 qHxL ‚ ci fi HxL f j HxL 0 - 2 f HxL f j HxL> „ x (47) Software para la resolución de EDO 57 y al sustituir en la ecuacion anterior se obtiene: n 1 0 = ‚ B‡ 9 pHxL f£ i HxL f£ j HxL + qHxL fi HxL f j HxL= „ x F ci 0 i =1 (48) ‡ 1 0 f HxL f j HxL „ x, j = 1, 2, ..., n. De estas ecuaciones se obtiene un sistema lineal A c = b de n µ n en las variables c1 , c2, ..., cn , donde esta matriz simétrica viene definida por 1 ai j = ‡ A pHxL f£ i HxL f£ j HxL + qHxL fi HxL f j HxLE „ x 0 bi = ‡ 0 1 f HxL f j HxL „ x. (49) La elección más elemental de las funciones básicas requiere la intervención de polinomios lineales seccionados. El primer paso es escoger puntos x0 , x1 , ... xn+1 para formar una partición dentro del intervalo @0, 1D de tal manera que 0 = x0 < x1 < ... < xn < xn+1 = 1. Al utilizar hi = xi+1 - xi para toda i = 0, 1, ..., n, se definen las funciones básicas f1 HxL, f2 HxL, ..., fn HxL mediante la expresión: 0 § x § xi-1 0, fi HxL = : x-xi-1 , hi-1 xi+1 -x , hi xi-1 < x § xi xi < x § xi+1 0, (50) xi+1 < x § 1 i = 1, 2, ..., n. Las funciones fi son lineales y seccionadas, por ello, aunque las derivadas fi £ , no Proyecto Fin de Carrera 58 son continuas, son constantes en el subintervalo abierto ( x j , x j+1 L para j = 0, 1, ..., n. Se obtiene, por tanto, 0 < x < xi-1 0, fi HxL = : £ 1 xi-1 < x < xi , hi-1 - h1 i , xi < x < xi+1 (51) xi+1 < x < 1 0, i = 1, 2, ..., n. Como fi y fi £ son distintos de cero solamente en (xi - 1, xi+1 L, fi HxL f j HxL ª 0 y fi £ HxL f j £ HxL ª 0, excepto cuando j toma un valor igual a i - 1, i, o i + 1. Por lo tanto, el sistema lineal dado en el teorema se reduce a un sistema lineal tridiagonal de n µ n. Los elementos de A que son distintos de cero son: ai, i = Ÿ0 9 pHxL@fi £ HxLD2 + qHxL@fi HxLD2 = „ x 1 = I h 1 M Ÿx pHxL „ x + I- h1 M Ÿx i+1 pHxL „ x i i i-1 i-1 2 2 xi x + I h 1 M Ÿ x Hx - xi-1 L2 qHxL „ x + I h1 M Ÿx i+1 Hxi+1 - xL2 qHxL „ x i i i-1 i-1 2 2 xi x para i = 1, 2, ..., n; ai ,i+1 = Ÿ0 9 pHxL fi £ HxL f£ i+1 HxL + qHxL fi £ HxL fi+1 HxL= „ x 1 = -I h1 M Ÿx i+1 pHxL „ x + I h1 M Ÿ x i+1 Hxi+1 - xL Hx - xi L qHxL „ x, i i i i 2 para i = 1, 2, ..., n - 1; x 2 x Software para la resolución de EDO 59 ai ,i-1 = Ÿ0 9 pHxL fi £ HxL f£ i-1 HxL + qHxL fi £ HxL fi-1 HxL= „ x 1 = -I h 1 M Ÿ x pHxL „ x + I h 1 M Ÿ x Hxi - xL Hx - xi-1 L qHxL „ x, i-1 i-1 i-1 i-1 2 2 xi xi para i = 1, 2, ..., n; Los valores de la matriz b son: bi = Ÿ0 f HxL fi HxL „ x = 1 1 hi-1 Ÿ xi-1 Hx - xi-1 L f HxL „ x + xi 1 hi i+1 Ÿ xi Hxi+1 - xL f HxL „ x, x para i = 1, 2, ..., n; Por lo tanto, se obtienen seis tipos de integrales a evaluar: Q1, i = Q2, i = Q3, i = Q4, i = Q5, i = Q6, i = 1 2 ‡ hi 2 1 hi-1 1 2 ‡ hi 2 1 xi+1 xi ‡ hi-1 ‡ 1 xi hi-1 1 hi ‡ ‡ xi-1 xi+1 xi xi xi-1 xi+1 xi Hxi+1 - xL Hx - xi L qHxL „ x, Hx - xi-1 L2 qHxL „ x, Hxi+1 - xL2 qHxL „ x, i = 1, 2, ..., n - 1, i = 1, 2, ..., n, i = 1, 2, ..., n, (52) xi pHxL „ x, i = 1, 2, ..., n + 1, xi-1 Hx - xi-1 L f HxL „ x, Hxi+1 - xL f HxL „ x, i = 1, 2, ..., n, i = 1, 2, ..., n. Proyecto Fin de Carrera 60 La matriz A y b del sistema lineal A c = b contienen los elementos: ai, i = Q4,i + Q4,i+1 + Q2, i + Q3, i , i = 1, 2, ..., n, ai,i+1 = -Q4,i+1 + Q1,i , i = 1, 2, ..., n - 1, ai,i-1 = - Q4,i + Q1-1, i = 2, 3, ..., n, bi = Q5,i + Q6,i , i = 1, 2, ..., n. (53) Los elementos de c son los coeficientes desconocidos c1 , c2 , ..., cn , a partir de los cuales se construye la aproximación de Rayleigh-Ritz f, dada por fHxL = ⁄ ni=1 ci fi HxL. En este método existe la dificultad práctica de tener que evaluar las 6 n integrales. Estas integrales puede evaluarse directamente o mediante una fórmula de cuadratura. La evaluación de la integral consiste en aproximar las funciones p, q y f con su polinomio interpolante lineal seccionado, e integrar luego la aproximación. Supóngse que se comienza por la integral de Q1,i . La interpolación lineal segmentaria de q es n+1 Pq HxL = ⁄ i=0 qHxi L fi HxL donde f1 , f2 , ..., fn están definidas en la fórmula (50) y además, f0 HxL = : x1 -x , x1 fn+1 HxL = : 0 § x § x1 0, entonces x-xn , 1-xn xn § x § 1 0, entonces Puesto que el intervalo de integración es @xi , xi+1 D, Pq se reduce a Software para la resolución de EDO 61 Pq HxL = qHxi L fi HxL + qHxi+1 L fi+1 HxL. La aproximación a Q1, i se obtiene integrando la aproximación al integrando Q1,i = I h1 M Ÿx i+1 Hxi+1 - xL Hx - xi L qHxL „ x i i 2 x º I h1 M Ÿ x i+1 Hxi+1 - xL Hx - xi LA i i 2 = x hi @qHxi L + qHxi+1 LD. 12 qHxi L Hxi+1 -xL hi + qHxi+1 L Hx-xi L E„x hi De la misma manera se realizan las aproximaciones a las integrales restantes, obteniéndose los siguientes resultados: Q1,i º Q2,i º Q3,i º Q4,i º Q5,i º Q6,i º @qHxi L + qHxi+1 LD 12 hi-1 @3 qHxi L + qHxi-1 LD 12 hi @3 qHxi L + qHxi+1 LD 12 hi-1 @ pHxi L + pHxi-1 LD 2 hi-1 @2 f Hxi L + f Hxi-1 LD 6 hi @2 f Hxi L + f Hxi+1 LD. 6 hi (54) En el algoritmo que se desarrolla a continuación se establece el sistema lineal tridiagonal donde se incorpora el algoritmo de factorización de Crout para resolver el sistema. Se aproxima la solución al problema de valor de frontera: „ - „x I pHxL „y M „y + qHxL y = f HxL, 0 § x § 1, y H0L = yH1L = 0 Proyecto Fin de Carrera 62 è Algoritmo 6. Método lineal segmentario de Rayleigh-Ritz Input HpHxL, qHxL, f HxL, nL vector xi , ci ,hi (* Se inicializan vectores y matrices *) x0 ≠ 0 For i = 1, ...., n do xi ≠ 0 ci ≠ 0 hi ≠ 0 End For i = 0, ..., n do hi ≠ xi+1 - xi End For i = 1, ..., n do 0 § x § xi-1 0, x-xi-1 , hi-1 xi+1 -x , hi fi HxL ô : xi-1 < x § xi xi < x § xi+1 xi+1 < x § 1 0, End (* Se calculan Q1, j , Q2, j , Q3, j , Q4, j , Q5, j , Q6, j *) For i = 1, ..., n - 1 do Q1,i ≠ Q2,i ≠ Q3,i ≠ Q4,i ≠ hi @qHxi L + qHxi+1 LD 12 hi-1 @3 qHxi L 12 hi @3 qHxi L 12 hi-1 @pHxi L 2 Q5,i ≠ hi-1 @2 6 Q6,i ≠ hi 6 + qHxi-1 LD + qHxi+1 LD + pHxi-1 LD f Hxi L + f Hxi-1 LD @2 f Hxi L + f Hxi+1 LD End (* Se calculan Q2,n , Q3,n , Q4,n , Q4,n+1 , Q5,n , Q6,n *) Q2,n ≠ Q3,n ≠ Q4,n ≠ hn-1 @3 qHxn L 12 hn @3 qHxn L 12 hn-1 @pHxn L 2 Q5,n ≠ hn-1 @2 6 Q6,n ≠ hn 6 + qHxn-1 LD + qHxn+1 LD + pHxn-1 LD f Hxn L + f Hxn-1 LD @2 f Hxn L + f Hxn+1 LD Software para la resolución de EDO 63 (* Creación del sitema lineal tridiagonal simétrico *) For i = 1, 2, ..., n - 1 do ai ≠ Q4,i + Q4,i+1 + Q2,i + Q3,i bi ≠ Q1,i + Q4,i+1 bi ≠ Q5,i + Q6,i End an ≠ Q4,n + Q4,n+1 + Q2,n + Q3,n bn ≠ Q5,n + Q6,n (* Resolución del sitema lineal tridiagonal simétrico *) a1 ≠ a1 b1 a1 z1 ≠ b z1 ≠ a1 1 For i = 2, ..., n - 1 do ai ≠ ai - bi-1 zi-1 zi ≠ bi ai zi ≠ Hbi - bi-1 zi-1 L ai End an ≠an - bn-1 zn-1 zn ≠ Hbn - bn-1 zn-1 L an cn ≠ zn For i = n - 1, ..., 1 do ci ≠ zi - zi ci+1 End (* Cálculo de la función lineal segmentaria aproximante f(x) *) fHxL ≠ ⁄ni=1 ci fi HxL Return HfHxLL Output Ejemplo. à Problema 5. Considérese el problema con valor de frontera „ - „x He-x y£ L + e-x y = Hx - 1L - Hx + 1L e-Hx-1L x œ @0, 1D, yH0L = 0, yH1L = 0 y su solución exacta y = xHex - eL. Aplíquese el método lineal segmentario de Rayleigh-Ritz para aproximar la solución f HxL. Proyecto Fin de Carrera 64 Método lineal segmentario de Rayleigh - Ritz para aproximar la solución al problema de valor de frontera. „y „ HpHxL L + qHxL y = f HxL „x „x ‰-x y + ‰-x „y „x - ‰-x „2 y „ x2 = x - ‰1-x Hx + 1L - 1 pHxL = ‰-x qHxL = ‰-x x œ @0., 1.D, yH0.L = 0, yH1.L = 0 f HxL = x - ‰1-x Hx + 1L - 1 Puntos. n = 19 x0 = 0. x1 h1 0.05 0.05 x2 h2 0.1 x3 h3 0.15 0.05 x4 h4 0.2 x5 h5 0.25 0.05 x6 h6 0.3 x7 h7 0.35 0.05 x8 h8 0.4 x9 h9 0.45 0.05 Hxi , hi L = x10 h10 = 0.5 0.05 0.05 0.05 0.05 0.05 x11 h11 0.55 0.05 x12 h12 0.6 x13 h13 0.65 0.05 x14 h14 0.7 x15 h15 0.75 0.05 x16 h16 0.8 x17 h17 0.85 0.05 x18 h18 0.9 x19 h19 0.95 0.05 0.05 0.05 0.05 0.05 xn+1 = 1. Integrales a evaluar. Q1, i =H 1 hi L2‡ xi+1 xi Hxi+1 -xLHx-xi LqHxL „x i = 1, 2,..., n-1. Software para la resolución de EDO 65 0.00773167892989 0.00735460049901 0.00699591239997 0.00665471772621 0.00633016331282 0.00602143760506 0.00572776862784 0.00544842205530 Q1, i = 0.00518269937615 0.00492993614483 0.00468950032202 0.00446079069256 0.00424323536325 0.00403629033268 0.00383943813018 0.00365218652294 0.00347406728447 0.00330463502367 Q2, i =H 1 hi-1 L2‡ xi xi-1 Hx-xi-1 L2 qHxL „x 0.0160539948995 0.0152710323292 0.0145262552940 0.0138178014636 0.0131438993339 0.0125028637990 0.0118930919363 0.0113130589980 0.0107613146000 Q2, i = 0.0102364790940 0.00973724011750 0.00926234931313 0.00881061920657 0.00838092023745 0.00797217793420 0.00758337022839 0.00721352489808 0.00686171713755 0.00652706724376 i = 1, 2,..., n. Proyecto Fin de Carrera Q3, i =H 66 1 hi L2‡ xi+1 xi Hxi+1 -xL2 qHxL „x i = 1, 2,..., n. 0.0156576162758 0.0148939853189 0.0141675970837 0.0134766352203 0.0128193719648 0.0121941638167 0.0115994474294 0.0110337357029 0.0104956140628 Q3, i = 0.00998373692465 0.00949682432916 0.00903365874132 0.00859308200560 0.00817399245081 0.00777534213490 0.00739613422427 0.00703542050173 0.00669229899497 0.00636591172154 Q4, i =H 1 hi-1 L2‡ xi xi-1 pHxL„x i = 1, 2,..., n+1. Software para la resolución de EDO 67 19.5082301997 18.5568025859 17.6517766444 16.7908893388 15.9719880026 15.1930249559 14.4520523852 13.7472174732 13.0767577655 Q4, i = 12.4389967637 11.8323397329 11.2552697146 10.7063437332 10.1841891878 9.68750042016 9.21503544952 8.76561286740 8.33810888325 7.93145451444 7.54463291322 Q5, i = 1 hi-1 ‡ xi xi-1 Hx-xi-1 Lf HxL „x -0.0920823543453 -0.0906464595925 -0.0890671552422 -0.0873588716292 -0.0855349728124 -0.0836078260911 -0.0815888674426 -0.0794886629483 -0.0773169664427 Q5, i = -0.0750827736090 -0.0727943727297 -0.0704593922905 -0.0680848456236 -0.0656771727653 -0.0632422796942 -0.0607855751060 -0.0583120048712 -0.0558260843146 -0.0533319284470 i = 1, 2,..., n. Proyecto Fin de Carrera Q6, i = 1 hi 68 ‡ xi+1 xi Hxi+1 -xLf HxL „x i = 1, 2,..., n. -0.0911418082118 -0.0896086461892 -0.0879418169777 -0.0861550321492 -0.0842609837696 -0.0822714112291 -0.0801971639778 -0.0780482604087 -0.0758339431140 Q6, i = -0.0735627307280 -0.0712424665587 -0.0688803641976 -0.0664830502873 -0.0640566046152 -0.0616065976921 -0.0591381259668 -0.0566558448167 -0.0541639994481 -0.0516664538317 Sistema tridiagonal simétrico: A.x = b. A= 38.0967 -18.5491 -17.6444 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 36.2387 -17.6444 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -16.7839 34.4714 -16.7839 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -15.9653 32.7902 -15.9653 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -15.1867 31.191 -15.1867 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -14.446 29.6698 -14.446 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -13.7415 28.2228 -13.7415 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -13.0713 26.8463 -13.0713 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -12.4338 25.537 -12.4338 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -11.8274 24.2916 -11.8274 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -11.2506 23.1068 -11.2506 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -10.7019 21.9799 -10.7019 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -10.1799 20.9079 -10.1799 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -9.68346 19.8882 -9.68346 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -9.2112 18.9183 -9.2112 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -8.76196 17.9956 -8.76196 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -8.33463 17.118 -8.33463 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -7.92815 16.2831 -7.92815 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -7.92815 15.489 Software para la resolución de EDO -0.183224 -0.180255 -0.177009 -0.173514 -0.169796 -0.165879 -0.161786 -0.157537 -0.153151 b = -0.148646 -0.144037 -0.13934 -0.134568 -0.129734 -0.124849 -0.119924 -0.114968 -0.10999 -0.104998 Solución al sistema lineal tridiagonal simétrico. c1 c2 c3 c4 c5 c6 c7 c8 c9 c = c10 c11 c12 c13 c14 c15 c16 c17 c18 c19 -0.0833579867539 -0.161325802637 -0.233488871405 -0.299404271441 -0.358598918782 -0.410567638309 -0.454771116422 -0.490633728118 -0.517541230961 = -0.534838318030 -0.541826021412 -0.537758957369 -0.521842403760 -0.493229199752 -0.451016457281 -0.394242073107 -0.321881029648 -0.232841472121 -0.125960548737 Tabla de errores en la aproximación. 69 Proyecto Fin de Carrera i xi 70 fi Hxi L = ci yHxi L »fHxi L - yHxi L» 1 0.0500000000 -0.0833579868 -0.0833505366 7.4501497537µ 10-6 2 0.1000000000 -0.1613258026 -0.1613110910 1.4711598641µ 10-5 3 0.1500000000 -0.2334888714 -0.2334671379 2.173354501µ 10-5 4 0.2000000000 -0.2994042714 -0.2993758141 2.8457380887µ 10-5 5 0.2500000000 -0.3585989188 -0.3585641029 3.4815839019µ 10-5 6 0.3000000000 -0.4105676383 -0.4105269063 4.0732044091µ 10-5 7 0.3500000000 -0.4547711164 -0.4547249980 4.611846945µ 10-5 8 0.4000000000 -0.4906337281 -0.4905828523 5.0875790496µ 10-5 9 0.4500000000 -0.5175412310 -0.5174863393 5.4891625123µ 10-5 10 0.5000000000 -0.5348383180 -0.5347802789 5.8039150726µ 10-5 11 0.5500000000 -0.5418260214 -0.5417658458 6.0175586367µ 10-5 12 0.6000000000 -0.5377589574 -0.5376978168 6.1140527621µ 10-5 13 0.6500000000 -0.5218424038 -0.5217816496 6.0754120577µ 10-5 14 0.7000000000 -0.4932291998 -0.4931703847 5.8815060138µ 10-5 15 0.7500000000 -0.4510164573 -0.4509613589 5.5098396669µ 10-5 16 0.8000000000 -0.3942420731 -0.3941927200 4.9353133337µ 10-5 17 0.8500000000 -0.3218810296 -0.3218397301 4.129959513µ 10-5 18 0.9000000000 -0.2328414721 -0.2328108456 3.0626548779µ 10-5 19 0.9500000000 -0.1259605487 -0.1259435607 1.6988050936µ 10-5 Gráfica de la aproximacion obtenida con el método lineal segmentario de Rayleigh - Ritz. Software para la resolución de EDO 71 Y 0.2 -0.1 -0.2 -0.3 -0.4 -0.5 0.4 0.6 0.8 1.0 X Proyecto Fin de Carrera 72 9.2. Método de trazadores cúbicos de Rayleigh-Ritz La matriz tridiagonal A dada por la funciones básicas es definida positiva, así que, el sistema lineal es estable respecto al error de redondeo. De acuerdo con todas las hipótesis formuladas se tiene: ° fHxL - yHxL ° = OIh2 M, para toda x en @0, 1D. Se utilizan las funciones lineales seccionadas básicas que producen una solución aproximada a la ecuación diferencial que describe el problema de valor de frontera del apartado anterior, que es continua pero no diferenciable en el intervalo [0, 1]. Sin embargo, se necesita un conjunto más complejo de funciones básicas para construir una aproximación que pertenezca C02 @0, 1D. Esto se consigue con unas funciones similares al los trazadores cúbicos interpolantes. Como definicion de un trazador cubico interpolante S en cinco nodos x0 , x1 , x2 , x3 y x4 para la función f se tiene: a) S es un polinomio cúbico (S j ) en el intervalo [ x j , x j+1 ] para toda j = 0, 1, 2, 3, obteniéndose 16 constantes para S , 4 para cada polinomio cúbico. b) SHx j L = f Hx j L, para j = 0, 1, 2, 3, 4. c) S j+1 Hx j+1 L = S j Hx j+1 L, para j = 0, 1, 2. d) S £ j+1 Hx j+1 L = S j £ Hx j+1 L, para j = 0, 1, 2. e) S ≥ j+1 Hx j+1 L = S ≥ j Hx j+1 L, para j = 0, 1, 2. Software para la resolución de EDO 73 f) Satisface una de las siguientes condiciones de frontera: Libre: S ≥ Hx0 L = S ≥ Hx4 L = 0 Sujeto: S £ Hx0 L = f £ Hx0 L y S £ Hx4 L = f £ Hx4 L. Las funciones de los trazadores cúbicos que se utilizan en estas funciones basicas reciben el nombre de trazadores B o trazadores en forma de campana que difieren de los trazadores interpolantes en que se satisfacen las condiciones de frontera descritas en el punto f . Se flexibilizan dos de las condiciones dadas en los puntos b al e. Ya que el trazador debe tener dos derivadas continuas en [ x0 , x4 ], se eliminan dos de las condiciones de interpolación. Se modifica la condición del punto b, quedando: b) SHx j L = f Hx j L para j = 0, 2, 4. El trazador B básico, S , que se define a continuación usa los siguientes nodos x0 = -2, x1 = -1, x2 = 0, x3 = 1 y x4 = 2, que satisfacen las condiciones: SHx0 L = 0, SHx2 L = 1, SHx4 L = 0 y también S ≥ Hx0 L = S ≥ Hx4 L = 0 y S £ Hx0 L = S £ Hx4 L = 0 En consecuencia, S e C 2 H-¶, ¶L. Proyecto Fin de Carrera 74 x § -2 0, SHxL = : 1 H2 + xL3 , 4 1 AH2 + xL3 - 4 H1 + xL3 E, 4 1 AH2 - xL3 - 4 H1 - xL3 E, 4 1 H2 - xL3 , 4 -2 § x § -1 -1 < x § 0 0< x§1 (55) 1<x§2 2<x 0, Para constuir las funciones básicas fi en C02 @0, 1D, primero se divide el intervalo [0,1] en intervalos uniformemente espaciados eligiendo un entero positivo n y definiendo un h = 1 . n+1 Se obtienen los nodos equiespaciados xi = i h, siendo i = 0, 1, ..., n, n + 1. Así las funciones básicas 8fi <n+1 i=0 se definen como sigue: SI hx M - 4 SI x+h M, h i=0 M - sI x+h M, SI x-h h h x-i h fi HxL = : SI h M, h SI x-n M - SI h i=1 2§i§n-1 x-Hn+2L h M, h x-Hn+1L h x-Hn+2L h SI h M - 4 SI h M, (56) i=n i= n+1 El conjunto 8fi <n+1 i=0 es un conjunto de trazadores cúbicos linealmente independientes que satisfacen fi H0L = fi H1L = 0 para i = 0, 1, ..., n, n + 1. Puesto que fi HxL y fi £ HxL son distintas de cero, solo con xi-2 § x § xi+2 , la matriz de aproximación de Rayleigh-Ritz es una matriz de banda con un ancho máximo de banda de siete: Software para la resolución de EDO a0,0 a1,0 A= a0,1 a1,1 a2,0 a2,1 a3,0 a3,1 a0,2 a1,2 75 a0,3 a1,3 a1,4 a2,2 a2,3 a3,2 a3,3 a2,4 a3,4 ∫ ∏ 0 a2,5 a3,5 ∏ 0 ∏ ª 0 ª a3,6 an-2,n+1 an-1,n+1 (57) an,n+1 ∫ 0 0 an+1,n-2 an+1,n-1 an+1,n an+1,n+1 donde ai j = Ÿ0 8 pHxL fi £ HxL f j £ HxL + qHxL fi HxL f j HxL< „ x 1 para i, j = 0, 1, ..., n + 1. La matriz A es definida positiva y se puede resolver el sistema lineal mediante el algoritmo de Choleski o mediante el método de la eliminación gaussiana. Se supone fHxL = ⁄n+1 i=0 ci fi HxL para toda x en el intervalo [0, 1]. En los nodos xi para i = 0, ..., n + 1, se tiene: f0 Hxi L = : 1 , 4 si i = 1 0, otro caso si i = 1 1, f1 Hxi L = : 14 , si i = 2 0, otro caso 1, si i = n 0, otro caso fn Hxi L = : 14 , si i = n - 1 fn+1 Hxi L = : 1 , 4 si i = n 0, otro caso y para j = 2, 3, ..., n - 1, Proyecto Fin de Carrera f j Hxi L = : 76 si i = j 1, 1 , 4 si i = j - 1 o i = j + 1 0, otro caso Como se puede observar a continuación en las gráficas, para algunos valores de f HxL. y SHxL y 1.0 0.8 0.6 0.4 0.2 −2 x −1 1 2 y φi@0D y φi@1D y 0.6 y 1.0 0.5 0.8 0.4 0.6 0.3 0.4 0.2 0.2 0.1 x 0.2 0.4 0.6 0.8 1.0 x 0.2 0.4 0.6 0.8 1.0 Software para la resolución de EDO 77 y φi@5D y 1.0 0.8 0.6 0.4 0.2 x 0.2 0.4 0.6 0.8 1.0 Gráficas de fi HxL. Figura 10 En el siguiente algoritmo se describe la construcción de la aproximación al trazador cúbico fHxL por el método de Rayleigh-Ritz para el problema con valor de frontera explicado anteriormente. è Algoritmo 7. Método de trazadores cúbicos Rayleigh-Ritz Se aproxima la solución al problema con valor de frontera „ - „x I pHxL „y M „x + qHxL y = f HxL, 0 § x § 1, con la suma de trazadores cúbicos fHxL = ⁄ ni=1 ci fi HxL. Input HpHxL, qHxL, f HxL, nL vector xi , hi ,ci (* Se inicializan vectores y matrices *) For i = 0, ...., n + 1 do xi ≠ 0 ci ≠ 0 hi ≠ 0 y H0L = yH1L = 0 Proyecto Fin de Carrera 78 End h≠ 1 n+1 For i = 0, ..., n + 1 do xi ≠ i h End x-2 ≠ 0 x-1 ≠ 0 xn+2 ≠ 1 xn+3 ≠ 1 (* Se define la funcion S *) 0, 1 H2 + xL3 , 4 1 AH2 + xL3 - 4 H1 + xL3 E, 4 1 AH2 - xL3 - 4 H1 - xL3 E, 4 1 H2 - xL3 , 4 SHxL ≠ : x § -2 -2 < x § -1 -1 < x § 0 f0 ≠ SI h M - 4 SJ f1 ≠ SI 1<x §2 2x 0, x 0< x §1 x+h N h x-x1 x+h M - SJ N h h For i = 2, ..., n - 1 do x-x fi ≠ SI h i M End fn ≠ SI x-xn h fn+1 ≠ SI M - SJ x-Hn+2L h N h x-xn+1 x-Hn+2L h M - 4 SJ N h h For i = 0, ..., n + 1 do For j = i, i + 1 , ..., mín H8i + 3, n + 1<L do L ≠ máxI9x j-2 , 0=M U ≠ mínH8xi+2 , 1<L ai j ≠ ŸL 9pHxL fi £ HxL f j £ HxL U + qHxL fi HxL f j HxL= „ x If i ∫ j then a j i ≠ ai j End If End If i ¥ 4 then For j = 0, ..., i - 4 do ai j ≠ 0 End Software para la resolución de EDO 79 End If If i § n - 3 then For j = i + 4, ..., n + 1 do ai j ≠ 0 End End If L ≠ máxH8xi-2 , 0<L U ≠ mínH8xi+2 , 1<L bi ≠ ŸL f HxL fi HxL „ x U End (* Se resuelve el sistema lineal de banda A c = b *) A ≠ Iai j Mi, j=0 n+1 b ≠ Hb0 , b1 , ..., bn+1 L T c ≠ Hc0 , c1 , ..., cn+1 LT c ≠ Cholesky HA, b, nL (* Cálculo de la función aproximante al trazador cúbico f(x) *) fHxL ≠ ⁄ni=1 ci fi HxL Return HfHxLL Output Ejemplo. à Problema 6. Considérese el problema con valor de frontera -x2 y≥ - 2 x y£ + 2 y = -4 x2 x œ @0, 1D, yH0L = 0, yH1L = 0 2 y su solución exacta y = x - x. Aplíquese el método de los trazadores cúbicos de Rayleigh-Ritz para aproximar la solución f HxL. -x2 y≥ - 2 x y£ + 2 y = -4 x2 f HxL = -4 x qHxL = 2 2 „ -x2 y≥ - 2 x y£ = - „x Ix2 „y MM - Ix2 „x „ - „x I pHxL y≥ + 2 xM y£ „y M „x + qHxL y = f HxL fl pHxL = x2 . Proyecto Fin de Carrera 80 Método de trazadores cúbicos de Rayleigh - Ritz para aproximar la solución al problema de valor de frontera. „y „ HpHxL L + qHxL y = f HxL „x „x - „2 y „x 2 x2 - 2 „y „x x + 2 y = -4 x 2 pHxL = x 2 qHxL = 2 f HxL = -4 x 2 x œ @0., 1.D, yH0.L = 0, yH1.L = 0 Puntos. n=9 x0 = 0. 0 x0 0.1 x1 0.2 x2 0.3 x3 0.4 x4 x Hxi L = 5 = 0.5 x6 0.6 x7 0.7 x8 0.8 x9 0.9 x10 1. Tabla de datos para el cálculo de aHi, jL. U k k+h SHai L, SHbi L i j L 0 0 0 0.2 0 0 0 0.2 0.1 0.2 0 0.1 0 1 0 0.2 0 1 0 0.2 0.1 0.2 0 0.1 0 2 0 0.2 0 2 0 0.2 0.1 0.2 0 0.1 0 3 0.1 0.2 0.1 0.2 fi HxL SHa j L, SHb j L 1. 1 JH2 - 10. xL3 - 4 H1 - 10. xL3 N - H2 - 10. Hx + 0.1LL3 2. 4 1 2. H2 - 10. xL3 3. 4 1. 1 3 3 JH2 - 10. xL - 4 H1 - 10. xL N - H2 - 10. Hx + 0.1LL3 2. 4 1 2. H2 - 10. xL3 3. 4 1 1. JH2 - 10. xL3 - 4 H1 - 10. xL3 N - H2 - 10. Hx + 0.1LL3 2. 4 1 2. H2 - 10. xL3 3. 4 1 2. H2 - 10. xL3 3. 4 ai, j = ‡ L U 1. 2. f j HxL 1 4 JH2 - 10. xL3 - 4 H1 - 10. xL3 N - H2 - 10. Hx + 0.1LL3 1 H2 - 10. xL3 4 1 0. 1 3 3 JH10. Hx - 0.1L + 2L - 4 H10. Hx - 0.1L + 1L N - H2 - 10. Hx + 0.1LL3 2. 4 4 1 1. JH2 - 10. Hx - 0.1LL3 - 4 H1 - 10. Hx - 0.1LL3 N 3. 4 1 -1. H10. Hx - 0.2L + 2L3 0 4 1 0. JH10. Hx - 0.2L + 2L3 - 4 H10. Hx - 0.2L + 1L3 N 0 4 1 -1. H10. Hx - 0.3L + 2L3 0 4 2. 3. HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H0,0L = 0.0785714 a H0,1L = 0.0861607 a H0,2L = -0.0367857 Software para la resolución de EDO 81 a H0,3L = -0.00419643 Tabla de datos para el cálculo de bHiL. k k+h SHai L, SHbi L 1. 0 0 0.2 0 0.1 2. 2. 0 0 0.2 0.1 0.2 3. i L fi HxL U bi = ‡ U L 1 4 IH2 - 10. xL3 - 4 H1 - 10. xL3 M - H2 - 10. Hx + 0.1LL3 1 4 H2 - 10. xL3 Hf HxL fi HxLL„x b H0L = -0.000933333 Tabla de datos para el cálculo de aHi, jL. U k k+h SHai L, SHbi L i j L 1 1 0 0.3 1 1 0 0.3 0.1 0.2 0 0.1 1 1 0 0.3 0.2 0.3 1 2 0 0.3 1 2 0 0.3 0.1 0.2 1 2 0 0.3 0.2 0.3 0 0.1 1 3 0.1 0.3 0.1 0.2 1 3 0.1 0.3 0.2 0.3 1 4 0.2 0.3 0.2 0.3 fi HxL SHa j L, SHb j L 1 0. 1 JH10. Hx - 0.1L + 2L3 - 4 H10. Hx - 0.1L + 1L3 N - H2 - 10. Hx + 0.1LL3 2. 4 4 1 1. JH2 - 10. Hx - 0.1LL3 - 4 H1 - 10. Hx - 0.1LL3 N 3. 4 1 2. H2 - 10. Hx - 0.1LL3 4. 4 1 0. 1 JH10. Hx - 0.1L + 2L3 - 4 H10. Hx - 0.1L + 1L3 N - H2 - 10. Hx + 0.1LL3 2. 4 4 1 1. JH2 - 10. Hx - 0.1LL3 - 4 H1 - 10. Hx - 0.1LL3 N 3. 4 1 2. H2 - 10. Hx - 0.1LL3 4. 4 1 1. 3 JH2 - 10. Hx - 0.1LL - 4 H1 - 10. Hx - 0.1LL3 N 3. 4 1 2. H2 - 10. Hx - 0.1LL3 4. 4 1 2. H2 - 10. Hx - 0.1LL3 4. 4 ai, j = ‡ L U HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H1,1L = 0.445 a H1,2L = 0.06125 a H1,3L = -0.173571 a H1,4L = -0.0116964 Tabla de datos para el cálculo de bHiL. f j HxL 1 0. 1 JH10. Hx - 0.1L + 2L3 - 4 H10. Hx - 0.1L + 1L3 N - H2 - 10. Hx + 0.1LL3 2. 4 4 1 1. JH2 - 10. Hx - 0.1LL3 - 4 H1 - 10. Hx - 0.1LL3 N 3. 4 1 2. H2 - 10. Hx - 0.1LL3 4. 4 1 -1. H10. Hx - 0.2L + 2L3 0 4 1 0. 3 JH10. Hx - 0.2L + 2L - 4 H10. Hx - 0.2L + 1L3 N 0 4 1 1. JH2 - 10. Hx - 0.2LL3 - 4 H1 - 10. Hx - 0.2LL3 N 0 4 1 -1. H10. Hx - 0.3L + 2L3 0 4 1 0. JH10. Hx - 0.3L + 2L3 - 4 H10. Hx - 0.3L + 1L3 N 0 4 1 -1. H10. Hx - 0.4L + 2L3 0 4 Proyecto Fin de Carrera 82 k k+h SHai L, SHbi L 0. 1 0 0.3 0 0.1 2. 1. 1 0 0.3 0.1 0.2 3. 2. 1 0 0.3 0.2 0.3 4. i L fi HxL U bi = ‡ U L 1 4 IH10. Hx - 0.1L + 2L - 4 H10. Hx - 0.1L + 1L M 3 3 1 4 1 4 H2 - 10. Hx + 0.1LL 3 IH2 - 10. Hx - 0.1LL - 4 H1 - 10. Hx - 0.1LL M 3 3 1 4 H2 - 10. Hx - 0.1LL 3 Hf HxL fi HxLL„x b H1L = -0.00796667 Tabla de datos para el cálculo de aHi, jL. U k k+h SHai L, SHbi L fi HxL SHa j L, SHb j L i j L 2 2 0 0.4 0 0.1 -1. 0 2 2 0 0.4 0.1 0.2 0. 0 1 2 2 0 0.4 0.2 0.3 1. 0 1 2 2 0 0.4 0.3 0.4 2. 0 2 3 0.1 0.4 0.1 0.2 0. 0 1 2 3 0.1 0.4 0.2 0.3 1. 0 1 2 3 0.1 0.4 0.3 0.4 2. 0 2 4 0.2 0.4 0.2 0.3 1. 0 2 4 0.2 0.4 0.3 0.4 2. 0 1 2 5 0.3 0.4 0.3 0.4 2. 0 1 ai, j = ‡ L U 1 4 4 4 4 IH2 - 10. Hx - 0.2LL - 4 H1 - 10. Hx - 0.2LL M 1. 0 1 3 3 H2 - 10. Hx - 0.2LL 4 4 3 IH2 - 10. Hx - 0.2LL - 4 H1 - 10. Hx - 0.2LL M 3 3 IH10. Hx - 0.2L + 2L - 4 H10. Hx - 0.2L + 1L M -1. 0 1 IH2 - 10. Hx - 0.2LL - 4 H1 - 10. Hx - 0.2LL M 0. 0 1 1. 0 1 3 3 3 3 H2 - 10. Hx - 0.2LL 3 IH2 - 10. Hx - 0.2LL - 4 H1 - 10. Hx - 0.2LL M 3 3 4 4 H2 - 10. Hx - 0.2LL 3 H2 - 10. Hx - 0.2LL 3 a H2,3L = -0.0516964 a H2,4L = -0.398571 a H2,5L = -0.0229464 Tabla de datos para el cálculo de bHiL. 4 4 0. 0 3 -1. 0 H10. Hx - 0.3L + 2L 3 IH2 - 10. Hx - 0.3LL - 4 H1 - 10. Hx - 0.3LL M 3 3 4 4 3 3 1 1 H2 - 10. Hx - 0.2LL IH10. Hx - 0.3L + 2L - 4 H10. Hx - 0.3L + 1L M -1. 0 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H2,2L = 0.901429 4 4 3 3 1 3 H10. Hx - 0.2L + 2L IH10. Hx - 0.2L + 2L - 4 H10. Hx - 0.2L + 1L M 2. 0 4 4 1 1 3 1 1 f j HxL -1. 0 0. 0 3 4 4 3 IH10. Hx - 0.2L + 2L - 4 H10. Hx - 0.2L + 1L M 1 4 H10. Hx - 0.2L + 2L H10. Hx - 0.4L + 2L 3 IH10. Hx - 0.4L + 2L - 4 H10. Hx - 0.4L + 1L M 3 3 1 4 H10. Hx - 0.5L + 2L 3 Software para la resolución de EDO i L U 2 0 0.4 2 0 0.4 2 0 0.4 2 0 0.4 83 k k+h SHai L, SHbi L -1. 0 0.1 0 0. 0.1 0.2 0 1. 0.2 0.3 0 2. 0.3 0.4 0 bi = ‡ U L fi HxL 1 4 H10. Hx - 0.2L + 2L3 1 4 IH10. Hx - 0.2L + 2L3 - 4 H10. Hx - 0.2L + 1L3 M 1 4 IH2 - 10. Hx - 0.2LL3 - 4 H1 - 10. Hx - 0.2LL3 M 1 4 H2 - 10. Hx - 0.2LL3 Hf HxL fi HxLL„x b H2L = -0.026 Tabla de datos para el cálculo de aHi, jL. i j L U k k+h SHai L, SHbi L fi HxL SHa j L, SHb j L 3 3 0.1 0.5 0.1 0.2 -1. 0 3 3 0.1 0.5 0.2 0.3 0. 0 1 3 3 0.1 0.5 0.3 0.4 1. 0 1 3 3 0.1 0.5 0.4 0.5 2. 0 3 4 0.2 0.5 0.2 0.3 0. 0 1 3 4 0.2 0.5 0.3 0.4 1. 0 1 3 4 0.2 0.5 0.4 0.5 2. 0 3 5 0.3 0.5 0.3 0.4 1. 0 3 5 0.3 0.5 0.4 0.5 2. 0 1 3 6 0.4 0.5 0.4 0.5 2. 0 1 ai, j = ‡ L U 1 4 4 4 4 IH2 - 10. Hx - 0.3LL - 4 H1 - 10. Hx - 0.3LL M 1. 0 1 3 3 H2 - 10. Hx - 0.3LL 4 4 3 IH2 - 10. Hx - 0.3LL - 4 H1 - 10. Hx - 0.3LL M 3 3 IH10. Hx - 0.3L + 2L - 4 H10. Hx - 0.3L + 1L M -1. 0 1 IH2 - 10. Hx - 0.3LL - 4 H1 - 10. Hx - 0.3LL M 0. 0 1 1. 0 1 3 3 3 3 H2 - 10. Hx - 0.3LL 3 IH2 - 10. Hx - 0.3LL - 4 H1 - 10. Hx - 0.3LL M 3 3 4 4 H2 - 10. Hx - 0.3LL 3 H2 - 10. Hx - 0.3LL 3 a H3,4L = -0.220446 a H3,5L = -0.713571 a H3,6L = -0.0379464 4 4 0. 0 3 -1. 0 H10. Hx - 0.4L + 2L 3 IH2 - 10. Hx - 0.4LL - 4 H1 - 10. Hx - 0.4LL M 3 3 4 4 3 3 1 1 H2 - 10. Hx - 0.3LL IH10. Hx - 0.4L + 2L - 4 H10. Hx - 0.4L + 1L M -1. 0 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H3,3L = 1.65143 4 4 3 3 1 3 H10. Hx - 0.3L + 2L IH10. Hx - 0.3L + 2L - 4 H10. Hx - 0.3L + 1L M 2. 0 4 4 1 1 3 1 1 f j HxL -1. 0 0. 0 3 4 4 3 IH10. Hx - 0.3L + 2L - 4 H10. Hx - 0.3L + 1L M 1 4 H10. Hx - 0.3L + 2L H10. Hx - 0.5L + 2L 3 IH10. Hx - 0.5L + 2L - 4 H10. Hx - 0.5L + 1L M 3 3 1 4 H10. Hx - 0.6L + 2L 3 Proyecto Fin de Carrera 84 Tabla de datos para el cálculo de bHiL. i L U 3 0.1 0.5 3 0.1 0.5 3 0.1 0.5 3 0.1 0.5 k k+h SHai L, SHbi L -1. 0.1 0.2 0 0. 0.2 0.3 0 1. 0.3 0.4 0 2. 0.4 0.5 0 bi = ‡ U L fi HxL 1 4 H10. Hx - 0.3L + 2L3 1 4 IH10. Hx - 0.3L + 2L3 - 4 H10. Hx - 0.3L + 1L3 M 1 4 IH2 - 10. Hx - 0.3LL3 - 4 H1 - 10. Hx - 0.3LL3 M 1 4 H2 - 10. Hx - 0.3LL3 Hf HxL fi HxLL„x b H3L = -0.056 Tabla de datos para el cálculo de aHi, jL. i j L U k k+h SHai L, SHbi L -1. 0 1 fi Hx L SHa j L, SHb j L H10. Hx - 0.4L + 2L3 -1. 0 4 4 0.2 0.6 0.2 0.3 4 4 0.2 0.6 0.3 0.4 0. 1 IH10. Hx - 0.4L + 2L3 - 4 H10. Hx - 0.4L + 1L3 M 0 4 4 4 0.2 0.6 0.4 0.5 1. 1 IH2 - 10. Hx - 0.4LL3 - 4 H1 - 10. Hx - 0.4LL3 M 0 4 0.6 2. 0 4 5 0.3 0.6 0.3 4 f j HxL 1 4 0. 1 IH10. Hx - 0.4L + 2L3 - 4 H10. Hx - 0.4L + 1L3 M 0 4 1. 1 IH2 - 10. Hx - 0.4LL3 - 4 H1 - 10. Hx - 0.4LL3 M 0 4 H2 - 10. Hx - 0.4LL3 2. 0 1 0.4 0. 1 IH10. Hx - 0.4L + 2L3 - 4 H10. Hx - 0.4L + 1L3 M 0 4 -1. 0 1 4 5 0.3 0.6 0.4 0.5 1. 1 IH2 - 10. Hx - 0.4LL3 - 4 H1 - 10. Hx - 0.4LL3 M 0 4 4 5 0.3 0.6 0.5 0.6 2. 0 0.5 1. 1 IH2 - 10. Hx - 0.4LL3 - 4 H1 - 10. Hx - 0.4LL3 M 0 4 4 6 0.4 0.6 0.5 0.6 2. 0 1 4 7 0.5 0.6 0.5 0.6 2. 0 1 4 4 0.2 0.6 0.5 4 6 0.4 0.6 0.4 ai, j = ‡ L U 1 4 1 4 H2 - 10. Hx - 0.4LL3 H10. Hx - 0.4L + 2L3 4 4 H2 - 10. Hx - 0.4LL3 H10. Hx - 0.5L + 2L3 0. 1 IH10. Hx - 0.5L + 2L3 - 4 H10. Hx - 0.5L + 1L3 M 0 4 1. 1 IH2 - 10. Hx - 0.5LL3 - 4 H1 - 10. Hx - 0.5LL3 M 0 4 -1. 0 1 4 H10. Hx - 0.6L + 2L3 -1.11022 µ 10-15 1 H2 - 10. Hx - 0.4LL3 IH10. Hx - 0.6L + 2L3 - 4 H10. Hx - 0.6L + 1L3 M 0 4 4 4 H2 - 10. Hx - 0.4LL3 -1. 0 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H4,4L = 2.70143 a H4,5L = -0.445446 a H4,6L = -1.11857 a H4,7L = -0.0566964 1 4 H10. Hx - 0.7L + 2L3 Software para la resolución de EDO 85 Tabla de datos para el cálculo de bHiL. i L U 4 0.2 0.6 4 0.2 0.6 4 0.2 0.6 4 0.2 0.6 k k+h SHai L, SHbi L -1. 0.2 0.3 0 0. 0.3 0.4 0 1. 0.4 0.5 0 2. 0.5 0.6 0 bi = ‡ U L fi HxL 1 4 H10. Hx - 0.4L + 2L3 1 4 IH10. Hx - 0.4L + 2L3 - 4 H10. Hx - 0.4L + 1L3 M 1 4 IH2 - 10. Hx - 0.4LL3 - 4 H1 - 10. Hx - 0.4LL3 M 1 4 H2 - 10. Hx - 0.4LL3 Hf HxL fi HxLL„x b H4L = -0.098 Tabla de datos para el cálculo de aHi, jL. i j L U k k+h SHai L, SHbi L -1. 0 1 fi Hx L SHa j L, SHb j L H10. Hx - 0.5L + 2L3 -1. 0 5 5 0.3 0.7 0.3 0.4 5 5 0.3 0.7 0.4 0.5 0. 1 IH10. Hx - 0.5L + 2L3 - 4 H10. Hx - 0.5L + 1L3 M 0 4 5 5 0.3 0.7 0.5 0.6 1. 1 IH2 - 10. Hx - 0.5LL3 - 4 H1 - 10. Hx - 0.5LL3 M 0 4 0.7 2. 0 5 6 0.4 0.7 0.4 4 f j HxL 1 4 H10. Hx - 0.5L + 2L3 0. 1 IH10. Hx - 0.5L + 2L3 - 4 H10. Hx - 0.5L + 1L3 M 0 4 1. 1 IH2 - 10. Hx - 0.5LL3 - 4 H1 - 10. Hx - 0.5LL3 M 0 4 H2 - 10. Hx - 0.5LL3 2. 0 1 0.5 0. 1 IH10. Hx - 0.5L + 2L3 - 4 H10. Hx - 0.5L + 1L3 M 0 4 -1. 0 1 5 6 0.4 0.7 0.5 0.6 1. 1 -1.11022 µ 10-15 1 IH2 - 10. Hx - 0.5LL3 - 4 H1 - 10. Hx - 0.5LL3 M IH10. Hx - 0.6L + 2L3 - 4 H10. Hx - 0.6L + 1L3 M 0 4 0 4 5 6 0.4 0.7 0.6 0.7 2. 0 5 7 0.5 0.7 0.5 0.6 1. 1 IH2 - 10. Hx - 0.5LL3 - 4 H1 - 10. Hx - 0.5LL3 M 0 4 0.7 2. 0 1 0.7 2. 0 1 5 5 0.3 0.7 0.6 5 7 0.5 0.7 0.6 5 8 0.6 0.7 0.6 ai, j = ‡ L U 1 4 1 4 4 4 H2 - 10. Hx - 0.5LL3 4 4 H2 - 10. Hx - 0.5LL3 -1. 0 1 4 0 4 a H5,6L = -0.726696 a H5,7L = -1.61357 a H5,8L = -0.0791964 H10. Hx - 0.7L + 2L3 IH10. Hx - 0.7L + 2L3 - 4 H10. Hx - 0.7L + 1L3 M -1. 0 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H5,5L = 4.05143 H10. Hx - 0.6L + 2L3 1. 1 IH2 - 10. Hx - 0.6LL3 - 4 H1 - 10. Hx - 0.6LL3 M 0 4 -15 1 3 -1.11022 µ 10 H2 - 10. Hx - 0.5LL H2 - 10. Hx - 0.5LL3 1 4 H10. Hx - 0.8L + 2L3 Proyecto Fin de Carrera 86 Tabla de datos para el cálculo de bHiL. i L k k+h SHai L, SHbi L -1. 0.3 0.4 0 0. 0.4 0.5 0 1. 0.5 0.6 0 2. 0.6 0.7 0 U 5 0.3 0.7 5 0.3 0.7 5 0.3 0.7 5 0.3 0.7 bi = ‡ U L fi HxL 1 4 H10. Hx - 0.5L + 2L 1 4 IH10. Hx - 0.5L + 2L - 4 H10. Hx - 0.5L + 1L M 1 4 IH2 - 10. Hx - 0.5LL - 4 H1 - 10. Hx - 0.5LL M 3 3 3 3 1 4 H2 - 10. Hx - 0.5LL Hf HxL fi HxLL„x b H5L = -0.152 Tabla de datos para el cálculo de aHi, jL. i j L U SHai L, SHbi L k k+h 6 6 0.4 0.8 0.4 0.5 6 6 0.4 0.8 0.5 0.6 6 6 0.4 0.8 0.6 0.7 6 6 0.4 0.8 0.7 0.8 6 7 0.5 0.8 0.5 0.6 -1. 0 1 4 fi HxL SHa j L, SHb j L H10. Hx - 0.6L + 2L3 -1. 0 f j HxL 1 4 H10. Hx - 0.6L + 2L3 -1.11022 µ 10-15 1 -1.11022 µ 10-15 1 IH10. Hx - 0.6L + 2L3 - 4 H10. Hx - 0.6L + 1L3 M IH10. Hx - 0.6L + 2L3 - 4 H10. Hx - 0.6L + 1L3 M 0 0 4 4 1. 1 IH2 - 10. Hx - 0.6LL3 - 4 H1 - 10. Hx - 0.6LL3 M 0 4 0 2. 0 1 IH10. Hx - 0.6L + 2L3 - 4 H10. Hx - 0.6L + 1L3 M -1. 0 1 1 4 4 1. 1 IH2 - 10. Hx - 0.6LL3 - 4 H1 - 10. Hx - 0.6LL3 M 0 4 H2 - 10. Hx - 0.6LL3 2. 0 -1.11022 µ 10-15 1 4 4 H2 - 10. Hx - 0.6LL3 H10. Hx - 0.7L + 2L3 6 7 0.5 0.8 0.6 0.7 1. 1 -1.11022 µ 10-15 1 IH2 - 10. Hx - 0.6LL3 - 4 H1 - 10. Hx - 0.6LL3 M IH10. Hx - 0.7L + 2L3 - 4 H10. Hx - 0.7L + 1L3 M 0 4 0 4 6 7 0.5 0.8 0.7 0.8 2. 0 6 8 0.6 0.8 0.6 0.7 1. 1 IH2 - 10. Hx - 0.6LL3 - 4 H1 - 10. Hx - 0.6LL3 M 0 4 6 8 0.6 0.8 0.7 0.8 2. 0 1 6 9 0.7 0.8 0.7 0.8 2. 0 1 ai, j = ‡ L U 1 4 4 4 H2 - 10. Hx - 0.6LL3 H2 - 10. Hx - 0.6LL3 H2 - 10. Hx - 0.6LL3 1. 1 IH2 - 10. Hx - 0.7LL3 - 4 H1 - 10. Hx - 0.7LL3 M 0 4 -1. 0 a H6,7L = -1.0642 a H6,8L = -2.19857 a H6,9L = -0.105446 1 4 H10. Hx - 0.8L + 2L3 0. 1 IH10. Hx - 0.8L + 2L3 - 4 H10. Hx - 0.8L + 1L3 M 0 4 -1. -3. HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H6,6L = 5.70143 3 1 4 H10. Hx - 0.9L + 2L3 3 Software para la resolución de EDO 87 Tabla de datos para el cálculo de bHiL. i L U k k+h SHai L, SHbi L -1. 0 6 0.4 0.8 0.4 0.5 6 0.4 0.8 0.5 0.6 -1.11022 µ 10 0 6 0.4 0.8 0.6 0.7 6 0.4 0.8 0.7 0.8 bi = ‡ U L -15 1. 0 2. 0 fi HxL 1 4 H10. Hx - 0.6L + 2L 1 4 JH10. Hx - 0.6L + 2L - 4 H10. Hx - 0.6L + 1L N 1 4 JH2 - 10. Hx - 0.6LL - 4 H1 - 10. Hx - 0.6LL N 3 3 3 3 1 4 H2 - 10. Hx - 0.6LL Hf HxL fi HxLL„x b H6L = -0.218 Tabla de datos para el cálculo de aHi, jL. i j L U k k+h SHai L, SHbi L -1. 0 1 fi HxL SHa j L, SHb j L H10. Hx - 0.7L + 2L3 -1. 0 7 7 0.5 0.9 0.5 0.6 7 7 0.5 0.9 0.6 0.7 7 7 0.5 0.9 0.7 0.8 1. 1 IH2 - 10. Hx - 0.7LL3 - 4 H1 - 10. Hx - 0.7LL3 M 0 4 0.9 2. 0 7 7 0.5 0.9 0.8 4 4 1 -1. 0 1 8 0.6 0.9 0.6 0.7 7 8 0.6 0.9 0.7 0.8 1. 1 IH2 - 10. Hx - 0.7LL3 - 4 H1 - 10. Hx - 0.7LL3 M 0 4 7 8 0.6 0.9 0.8 0.9 2. 0 0.8 1. 1 IH2 - 10. Hx - 0.7LL3 - 4 H1 - 10. Hx - 0.7LL3 M 0 4 0.9 2. 0 1 0.9 2. 0 1 7 9 0.7 0.9 0.8 7 10 0.8 0.9 0.8 H10. Hx - 0.7L + 2L3 ai, j = ‡ L U 1 4 4 4 1. 1 IH2 - 10. Hx - 0.7LL3 - 4 H1 - 10. Hx - 0.7LL3 M 0 4 H2 - 10. Hx - 0.7LL3 7 9 0.7 0.9 0.7 4 2. 0 0. 1 IH10. Hx - 0.7L + 2L3 - 4 H10. Hx - 0.7L + 1L3 M 0 4 7 f j HxL 1 -1.11022 µ 10-15 1 -1.11022 µ 10-15 1 IH10. Hx - 0.7L + 2L3 - 4 H10. Hx - 0.7L + 1L3 M IH10. Hx - 0.7L + 2L3 - 4 H10. Hx - 0.7L + 1L3 M 0 0 4 4 1 H2 - 10. Hx - 0.7LL3 a H7,8L = -1.45795 a H7,9L = -2.87357 a H7,10L = -0.135446 4 4 H2 - 10. Hx - 0.7LL3 H10. Hx - 0.8L + 2L3 0. 1 IH10. Hx - 0.8L + 2L3 - 4 H10. Hx - 0.8L + 1L3 M 0 4 1. 1 IH2 - 10. Hx - 0.8LL3 - 4 H1 - 10. Hx - 0.8LL3 M 0 4 -1. -3. 1 4 H10. Hx - 0.9L + 2L3 H2 - 10. Hx - 0.7LL 0. 1 IH10. Hx - 0.9L + 2L3 - 4 H10. Hx - 0.9L + 1L3 M -2. 4 H2 - 10. Hx - 0.7LL3 -1. -2. 3 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H7,7L = 7.65143 3 1 4 H10. Hx - 1.L + 2L3 3 Proyecto Fin de Carrera 88 Tabla de datos para el cálculo de bHiL. i L U SHai L, SHbi L -1. 0 k k+h 7 0.5 0.9 0.5 0.6 -15 0.7 -1.11022µ 10 0 1. 0.8 0 2. 0.9 0 7 0.5 0.9 0.6 7 0.5 0.9 0.7 7 0.5 0.9 0.8 bi = ‡ U L fi Hx 1 4 H10. Hx - 0.7L + 2L 3 1 4 IH10. Hx - 0.7L + 2L - 4 H10. Hx - 0.7L + 1L 3 1 4 IH2 - 10. Hx - 0.7LL - 4 H1 - 10. Hx - 0.7LL 3 3 3 1 4 H2 - 10. Hx - 0.7LL 3 Hf HxL fi HxLL„x b H7L = -0.296 Tabla de datos para el cálculo de aHi, jL. i j L U k k+h SHai L, SHbi L fi Hx L SHa j L, SHb j L f j HxL H10. Hx - 0.8L + 2L3 -1. 0 0.8 0. 1 IH10. Hx - 0.8L + 2L3 - 4 H10. Hx - 0.8L + 1L3 M 0 4 0. 0 1 8 0.6 1. 0.8 0.9 1. 1 IH2 - 10. Hx - 0.8LL3 - 4 H1 - 10. Hx - 0.8LL3 M 0 4 1. 0 1 8 8 0.6 1. 0.9 1. H2 - 10. Hx - 0.8LL3 2. 0 8 9 0.7 1. 0.7 0.8 0. 1 IH10. Hx - 0.8L + 2L3 - 4 H10. Hx - 0.8L + 1L3 M 0 4 -1. -3. 0.9 1. 1 IH2 - 10. Hx - 0.8LL3 - 4 H1 - 10. Hx - 0.8LL3 M 0 4 0. -2. 8 8 0.6 1. 0.6 0.7 8 8 0.6 1. 0.7 8 8 8 9 0.7 1. 0.8 9 0.7 1. 0.9 -1. 0 0.9 8 10 0.8 1. 0.9 1. 4 2. 0 1 4 2. 0 1. 8 10 0.8 1. 0.8 1 1 4 -1. -2. H2 - 10. Hx - 0.8LL3 0. -1. L U 1 4 4 4 4 a H8,9L = -1.73875 a H8,10L = -2.96179 Tabla de datos para el cálculo de bHiL. IH2 - 10. Hx - 0.8LL3 - 4 H1 - 10. Hx - 0.8LL3 M 4 1 4 4 H2 - 10. Hx - 0.8LL3 H10. Hx - 0.9L + 2L3 IH10. Hx - 0.9L + 2L3 - 4 H10. Hx - 0.9L + 1L3 M 1 4 1 4 H10. Hx - 1.L + 2L3 IH10. Hx - 1.L + 2L3 - 4 H10. Hx - 1.L + 1L3 M - H10. Hx - 1.1L + 2L3 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H8,8L = 9.90143 IH10. Hx - 0.8L + 2L3 - 4 H10. Hx - 0.8L + 1L3 M 1 1 H10. Hx - 0.8L + 2L3 1 1. 1 IH2 - 10. Hx - 0.9LL3 - 4 H1 - 10. Hx - 0.9LL3 M - H10. Hx - 1.1L + 2L3 -1. 4 4 1. 1 IH2 - 10. Hx - 0.8LL3 - 4 H1 - 10. Hx - 0.8LL3 M 0 4 2. 0 ai, j = ‡ H2 - 10. Hx - 0.8LL 3 1 Software para la resolución de EDO i L U 8 0.6 1. 8 0.6 1. 8 0.6 1. 8 0.6 1. 89 k k+h SHai L, SHbi L -1. 0.6 0.7 0 0. 0.7 0.8 0 1. 0.8 0.9 0 2. 0.9 1. 0 bi = ‡ U L fi HxL 1 4 H10. Hx - 0.8L + 2L3 1 4 IH10. Hx - 0.8L + 2L3 - 4 H10. Hx - 0.8L + 1L3 M 1 4 IH2 - 10. Hx - 0.8LL3 - 4 H1 - 10. Hx - 0.8LL3 M 1 4 H2 - 10. Hx - 0.8LL3 Hf HxL fi HxLL„x b H8L = -0.386 Tabla de datos para el cálculo de aHi, jL. j 9 0.7 1 0.7 0.8 -1. -3. 9 9 0.7 1 0.8 0.9 0. -2. 9 L U k k+h SHai L, SHbi L i 9 9 0.7 1 0.9 1. 9 10 0.8 1 0.8 0.9 9 10 0.8 1 0.9 1. fi HxL SHa j L, SHb j L 1 H10. Hx - 0.9L + 2L3 -1. -3. JH10. Hx - 0.9L + 2L3 - 4 H10. Hx - 0.9L + 1L3 N 0. -2. 4 1 4 1 1 1. JH2 - 10. Hx - 0.9LL3 - 4 H1 - 10. Hx - 0.9LL3 N - H10. Hx - 1.1L + 2L3 -1. 4 4 1 0. JH10. Hx - 0.9L + 2L3 - 4 H10. Hx - 0.9L + 1L3 N -2. 4 1 1 1. JH2 - 10. Hx - 0.9LL3 - 4 H1 - 10. Hx - 0.9LL3 N - H10. Hx - 1.1L + 2L3 -1. 4 4 ai, j = ‡ L U f j HxL 1 4 1 4 H10. Hx - 0.9L + 2L3 JH10. Hx - 0.9L + 2L3 - 4 H10. Hx - 0.9L + 1L3 N 1 1 1. JH2 - 10. Hx - 0.9LL3 - 4 H1 - 10. Hx - 0.9LL3 N - H10. Hx - 1.1L + 2L3 -1. 4 4 1 -1. H10. Hx - 1.L + 2L3 -2. 4 1 0. 3 3 JH10. Hx - 1.L + 2L - 4 H10. Hx - 1.L + 1L N - H10. Hx - 1.1L + 2L3 -1. 4 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H9,9L = 16.645 a H9,10L = 7.82991 Tabla de datos para el cálculo de bHiL. k k+h SHai L, SHbi L -1. 9 0.7 1 0.7 0.8 -3. 0. 9 0.7 1 0.8 0.9 -2. 1. 9 0.7 1 0.9 1. -1. i fi HxL L U bi = ‡ L U 1 4 1 4 1 4 Hf HxL fi HxLL„x 3 IH10. Hx - 0.9L + 2L - 4 H10. Hx - 0.9L + 1L M 3 IH2 - 10. Hx - 0.9LL - 4 H1 - 10. Hx - 0.9LL M 3 H10. Hx - 0.9L + 2L 3 3 1 4 H10. Hx - 1.1L + 2L 3 Proyecto Fin de Carrera 90 b H9L = -0.437967 Tabla de datos para el cálculo de aHi, jL. i j L U k k+h SHai L, SHbi L 10 10 0.8 1 0.8 0.9 10 10 0.8 1 0.9 1. fi HxL SHa j L, SHb j L 1 -1. -2. H10. Hx - 1.L + 2L3 4 1 0. JH10. Hx - 1.L + 2L3 - 4 H10. Hx - 1.L + 1L3 N - H10. Hx - 1.1L + 2L3 -1. 4 ai, j = ‡ L U f j HxL 1 -1. -2. H10. Hx - 1.L + 2L3 4 1 0. JH10. Hx - 1.L + 2L3 - 4 H10. Hx - 1.L + 1L3 N - H10. Hx - 1.1L + 2L3 -1. 4 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H10,10L = 14.1786 Tabla de datos para el cálculo de bHiL. k k+h SHai L, SHbi L -1. 0.9 -2. 0. 10 0.8 1 0.9 1. -1. i fi HxL L U 1 4 10 0.8 1 0.8 bi = ‡ U L 1 4 H10. Hx - 1.L + 2L 3 IH10. Hx - 1.L + 2L - 4 H10. Hx - 1.L + 1L M - H10. Hx - 1.1L + 2L 3 3 3 Hf HxL fi HxLL„x b H10L = -0.176933 Sistema con una matriz simétrica en banda: A.x = b. A= 0.0785714 0.0861607 -0.0367857 -0.00419643 0 0 0 0 0 0 0.0861607 0.445 0.06125 -0.173571 -0.0116964 0 0 0 0 0 0 -0.0367857 0.06125 0.901429 -0.0516964 -0.398571 -0.0229464 0 0 0 0 0 -0.00419643 -0.173571 -0.0516964 1.65143 0 -0.0116964 -0.398571 -0.220446 0 0 -0.0229464 -0.713571 0 0 0 -0.0379464 0 -0.220446 -0.713571 -0.0379464 0 0 0 0 2.70143 -0.445446 -1.11857 -0.0566964 0 0 0 -0.445446 4.05143 -0.726696 -1.61357 -0.0791964 0 0 -1.11857 -0.726696 5.70143 -1.0642 -2.19857 -1.0642 7.65143 -1.45795 -2.87357 -0.135446 -1.45795 9.90143 -1.73875 -2.96179 0 0 0 0 -0.0566964 -1.61357 0 0 0 0 0 -0.0791964 -2.19857 -0.105446 0 0 0 0 0 0 0 -0.105446 -2.87357 -1.73875 16.645 7.82991 0 0 0 0 0 0 0 -0.135446 -2.96179 7.82991 14.1786 Software para la resolución de EDO -0.000933333 -0.00796667 -0.026 -0.056 -0.098 b = -0.152 -0.218 -0.296 -0.386 -0.437967 -0.176933 Solución al sistema lineal simétrico. Se aplica el método de Cholesky. La matriz A es definida positiva. c0 c1 c2 c3 c4 c = c5 c6 c7 c8 c9 c10 -0.00222222222147 -0.0622222222237 -0.108888888890 -0.142222222226 -0.162222222225 = -0.168888888894 -0.162222222225 -0.142222222224 -0.108888888891 -0.0622222222165 -0.00222222223236 0 -0.0933333333355 -0.163333333335 -0.213333333339 -0.243333333338 f Hxi L = -0.253333333341 -0.243333333337 -0.213333333336 -0.163333333336 -0.0933333333247 -7.77156120782µ 10-18 91 Proyecto Fin de Carrera 92 n+1 f HxL = ‚ ci HxL fi HxL = i=0 -0.00222222 4 H10. Hx - 1.1L + 1L3 - H10. Hx - 1.1L + 2L3 + 1 4 1 4 1 4 1 4 1 4 1 4 1 4 1 4 1 4 1 4 IH2 - 10. Hx - 1.LL3 - 4 H1 - 10. Hx - 1.LL3 M + -0.0622222 IH2 - 10. Hx - 0.9LL3 - 4 H1 - 10. Hx - 0.9LL3 M - 1 4 H10. Hx - 1.1L + 2L3 + -0.108889 IH2 - 10. Hx - 0.8LL3 - 4 H1 - 10. Hx - 0.8LL3 M + -0.142222 IH2 - 10. Hx - 0.7LL - 4 H1 - 10. Hx - 0.7LL M + 3 3 -0.162222 IH2 - 10. Hx - 0.6LL3 - 4 H1 - 10. Hx - 0.6LL3 M + -0.168889 IH2 - 10. Hx - 0.5LL - 4 H1 - 10. Hx - 0.5LL M + 3 3 -0.162222 IH2 - 10. Hx - 0.4LL3 - 4 H1 - 10. Hx - 0.4LL3 M + -0.142222 IH2 - 10. Hx - 0.3LL3 - 4 H1 - 10. Hx - 0.3LL3 M + -0.108889 IH2 - 10. Hx - 0.2LL3 - 4 H1 - 10. Hx - 0.2LL3 M + -0.0622222 IH2 - 10. Hx - 0.1LL3 - 4 H1 - 10. Hx - 0.1LL3 M + -0.00222222 1 4 IH2 - 10. xL3 - 4 H1 - 10. xL3 M - H2 - 10. Hx + 0.1LL3 Tabla de errores en la aproximación con el método. i 0 1 2 3 4 5 6 7 8 9 10 xi ci 0 -0.0022222222 0.1 -0.0622222222 0.2 -0.1088888889 0.3 -0.1422222222 0.4 -0.1622222222 0.5 -0.1688888889 0.6 -0.1622222222 0.7 -0.1422222222 0.8 -0.1088888889 0.9 -0.0622222222 1. -0.0022222222 fHxi L 0.0000000000 -0.0900000000 -0.1600000000 -0.2100000000 -0.2400000000 -0.2500000000 -0.2400000000 -0.2100000000 -0.1600000000 -0.0900000000 0.0000000000 yHxi L 0.0000000000 -0.0900000000 -0.1600000000 -0.2100000000 -0.2400000000 -0.2500000000 -0.2400000000 -0.2100000000 -0.1600000000 -0.0900000000 0.0000000000 »fHxi L - yHxi L» 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. Gráficas de la aproximación f HxL cúbica de Rayleigh - Ritz y la solución exacta. Software para la resolución de EDO 93 y x2 - x y fHxL y -0.05 y 0.2 0.4 0.6 0.8 1.0 x -0.05 -0.10 -0.10 -0.15 -0.15 -0.20 -0.20 -0.25 -0.25 0.2 0.4 0.6 0.8 1.0 x 9.2.1. Método de Cholesky El metodo de factorizacion de Cholesky es utilizado para resolver los sistemas de ecuaciones de tipo A x = b, donde la matriz A es definida positiva, que a menudo aparecen en este tipo de problemas. Para factorizar esta matriz A en L L£ , donde L es una matriz triangular inferior, se aplica el siguiente método: Algoritmo de factorización de Cholesky Input IIai j M, Hbi L, nM l1,1 ≠ a1,1 For i = 2, 3, ..., n do l j i ≠ a j i ë l1,1 End For i = 1, 2, 3, ..., n do i-1 1ê2 li i ≠ ai i - S li2k k=1 For j = i + 1, i + 2, ..., n do l j i ≠ a j i - S l j k .li k ì li i i-1 k=1 End End i-1 ln n ≠ an n - S ln2 k k=1 1ê2 Proyecto Fin de Carrera 94 y1 ≠ b1 ë l1,1 For i = 2, ..., n do yi ≠ bi - S l i j y j ì l i i i-1 k=1 End xn ≠ yn ê ln n For i = n - 1, ..., 1 do xi ≠ yi - S l j i x j ì l i i n j=i+1 End Return H xi L Output Software para la resolución de EDO 95 10. Estudio de la arquitectura En esta sección se analiza la arquitectura propuesta para la correcta implantación de la plataforma de desarrollo del proyecto. Como soporte software, en primer lugar, se propone un sistema operativo comercial, como Windows XP, Windows Vista, Machintosh, etc. Es necesaria también una herramienta matemática para la programación de la aplicación, en este caso Mathematica en su versión 6.0, y el paquete gráfico The Super Widget Package (SWP) para la creación de la interfaz de usuario (GUI). Para la ejecución de la aplicación es necesario contar también con la JVM (Java Virtual Machine) ya que utiliza un núcleo Java para la ejecución de las interfaces y por último, un software que permita la generación de ficheros PDF para la impresión de la documentación en formato digital, como por ejemplo PDFCreator. Proyecto Fin de Carrera 96 11. Diseño externo A continuación se describe el diseño de las ventanas de la interfaz de usuario que se ha desarrollado para esta aplicación, incluyendo una descripción y características generales de cada una de las ventanas. Se puede observar que se trata de una interfaz muy sencilla que hace que la realización de operaciones sea fácil y cómoda para el usuario final. Ventana de la aplicación Aproximación de Ecuaciones Diferenciales. Figura 11 Software para la resolución de EDO 97 11.1. Métodos lineales Método del disparo lineal. En esta ventana se encuentran diferentes casillas de texto donde se introducen los parámetros necesarios para la ejecución de este método. La ecuación debe de ser introducida en la forma y≥ = pHxL y£ + qHxL y + rHxL, que se indica en la parte superior derecha de la ventana. Existe también otra casilla de texto donde se puede introducir de manera opcional la ecuación real para hacer una comparativa a posteriori del error cometido por el método. A continuación existen cuatro casillas de texto donde se introducen el intervalo y los valores de frontera correspondientes a dicho intervalo. Por último el tamaño del paso por el que será dividido el intervalo. En la parte inferior de la ventana se encuentran los botones “Método” y “Salir”. Al hacer clic sobre “Método” se inicia el proceso del cálculo de la aproximación, el cual una vez concluido, mostrará los resultados en la parte izquierda de la ventana, mediante una gráfica donde se representa la solución real y la obtenida y debajo de ésta, en rojo, los puntos de la aproximación. Al hacer clic en “Salir” se cierra la ventana y se vuelve a la ventana principal. A continuación se muestra la ventana y la ejecución en un ejercicio. Proyecto Fin de Carrera 98 ô En el ejemplo se han tomado los siguientes datos: y≥ = y£ + 2 y + cosHxL donde pHxL = 1, qHxL = 2 y rHxL = cosHxL, definida en el intervalo A0, p E 2 con unos valores de frontera f HaL = -0.3 y f HbL = -0.1 y un tamaño de paso de p8 . La solución exacta a la ecuación diferencia es y = 1 10 HsenHxL + 3 cosHxLL, la cual se puede ver representada en la gráfica en la parte izquierda de la ventana en azul junto a la representación de la aproximación obtenida en color rojo. Ventana : M étodo del disparo lineal. Figura 12 Se obtiene, también, en un fichero aparte los resultados de la ejecución del método. Software para la resolución de EDO 99 Método del disparo lineal para el problema con valor de frontera: y≥ = 1.y£ + 2.y + cosHxL x œ @0., 1.5708D, yH0.L = -0.3, i xi 0 1 2 3 4 0.0000000000 0.3926990817 0.7853981634 1.1780972451 1.5707963268 u1,i -0.3000000000 -0.2650158208 -0.1383948423 0.1321628120 0.6588350398 yH1.5708L = -0.1 v1,i h = 0.392699 w1,i 0.0000000000 0.5050394157 1.4473056289 3.4005282847 7.6041297787 w2,i -0.3000000000 -0.3154149613 -0.2828250738 -0.2071843706 -0.1000000000 -0.0997924893 0.0225360287 0.1414535329 0.2388551820 0.2999187862 Tabla de errores xi w1,i yHxi L »w1,i - yHxi L» 0.0000000000 -0.3000000000 -0.3000000000 0.3926990817 -0.3154149613 -0.3154322030 0.0000000000 0.0000172417 0.7853981634 -0.2828250738 -0.2828427125 0.0000176386 1.1780972451 -0.2071843706 -0.2071929830 1.5707963268 -0.1000000000 -0.1000000000 8.6123787982µ 10-6 0.0000000000 Método de las diferencias finitas. El diseño de esta ventana es muy similar a la del método del disparo lineal. En ella se encuentran también diferentes casillas de texto donde se introducen los parámetros necesarios para la ejecución de este método. La ecuación debe de ser introducida en la forma y≥ = pHxL y£ + qHxL y + rHxL, que se indica en la parte superior derecha de la ventana. Existe también otra casilla de texto donde se puede introducir de manera opcional la ecuación real para hacer una comparativa a posteriori del error cometido por el método. A continuación existen cuatro casillas de texto donde se introducen el intervalo y Proyecto Fin de Carrera 100 los valores de frontera correspondientes a dicho intervalo. Por último el tamaño del paso por el que será dividido el intervalo. En la parte inferior de la ventana se encuentran los botones “Método” y “Salir”. Al hacer clic sobre “Método” se inicia el proceso del cálculo de la aproximación, el cual una vez concluido, mostrará los resultados en la parte izquierda de la ventana, mediante una gráfica donde se representa la solución real y la obtenida y debajo de ésta, en rojo, los puntos de la aproximación. Al hacer clic en “Salir” se cierra la ventana y se vuelve a la ventana principal. A continuación se muestra la ventana y la ejecución en un ejercicio. ô En el ejemplo se toman los siguientes datos: y≥ = 2 y£ - y + x e x - x donde pHxL = 2, qHxL = -1 y rHxL = x e x - x definida en el intervalo @0, 2D con unos valores de frontera f HaL = 0 y f HbL = -4 y un tamaño de paso de 0.2. La ecuación solución exacta es y = 1 6 x3 e x - 5 3 x e x + 2 e x - x - 2, la cual se puede ver representada en la gráfica en la parte izquierda de la ventana en azul junto a la representación de la aproximación obtenida en color rojo. Software para la resolución de EDO Ventana : M étodo de las diferencia finitas. Figura 13 Se obtiene, también, en un fichero aparte los resultados de la ejecución del método. Método de las diferencias finitas para el problema con valor de frontera: y≥ = 2.y£ + -1.y + ‰x x - x x œ @0., 2.D, yH0.L = 0., yH2.L = -4. h = 0.2 i 0 1 2 3 xi 0.0000000000 0.2000000000 0.4000000000 0.6000000000 wi 0.0000000000 -0.1603338739 -0.3906039636 -0.7066424059 4 0.8000000000 -1.1207043851 5 1.0000000000 -1.6367404975 6 1.2000000000 -2.2430435498 7 1.4000000000 -2.9011389354 8 1.6000000000 -3.5293610693 9 10 1.8000000000 -3.9789836227 2.0000000000 -4.0000000000 101 Proyecto Fin de Carrera 102 Tabla de errores xi 0.0000000000 wi 0.0000000000 yHxi L »wi - yHxi L» 0.0000000000 0. 0.2000000000 -0.1603338739 -0.1627001994 2.3663254409µ 10-3 0.4000000000 -0.3906039636 -0.3949876064 4.3836427792µ 10-3 0.6000000000 -0.7066424059 -0.7122849228 5.6425168725µ 10-3 0.8000000000 -1.1207043851 -1.1263932218 5.6888366605µ 10-3 1.0000000000 -1.6367404975 -1.6408590858 4.1185882674µ 10-3 1.2000000000 -2.2430435498 -2.2438063263 7.6277646196µ 10-4 1.4000000000 -2.9011389354 -2.8971552041 3.9837312552µ 10-3 1.6000000000 -3.5293610693 -3.5207514812 8.6095880741µ 10-3 1.8000000000 -3.9789836227 -3.9693901290 9.5934937405µ 10-3 2.0000000000 -4.0000000000 -4.0000000000 0. Software para la resolución de EDO 103 11.2. Métodos no lineales Método del disparo no lineal. En esta ventana se encuentran diferentes casillas de texto donde se introducen los parámetros necesarios para la ejecución de este método. La ecuación debe de ser introducida en la forma y≥ = f HxL y£ , que se indica en la parte superior derecha de la ventana. Existe también otra casilla de texto donde se puede introducir de manera opcional la ecuación real para hacer una comparativa a posteriori del error cometido por el método. A continuación existen cuatro casillas de texto donde se introducen el intervalo y los valores de frontera correspondientes a dicho intervalo. Por último el tamaño del paso por el que será dividido el intervalo. En la parte inferior de la ventana se encuentran los botones “Método” y “Salir”. Al hacer clic sobre “Método” se inicia el proceso del cálculo de la aproximación, el cual una vez concluido, mostrará los resultados en la parte izquierda de la ventana, mediante una gráfica donde se representa la solución real y la obtenida y debajo de ésta, en rojo, los puntos de la aproximación. Al hacer clic en “Salir” se cierra la ventana y se vuelve a la ventana principal. A continuación se muestra la ventana y la ejecución en un ejercicio. Proyecto Fin de Carrera ô 104 En el ejemplo se toman los siguientes datos: y≥ = 1 8 I32 + 2 x3 - y y£ M donde f HxL = 1 8 I32 + 2 x3 - y y£ M definida en el intervalo @1, 3D con unos valores de frontera f HaL = 17 y f HbL = 43 3 y un tamaño de paso de h = 0.2. La ecuación real dada es y = x2 + 16 , x la cual se puede ver representada en la gráfica en la parte izquierda de la ventana en azul junto a la representación de la aproximación obtenida en color rojo. Ventana : M étodo del disparo no lineal. Figura 14 Software para la resolución de EDO 105 Se obtiene, también, en un fichero aparte los resultados de la ejecución del método. Método del disparo no lineal para el problema con valor de frontera: 1 y≥ = I2 x 3 - y z + 32M 8 x œ @1., 3.D, yH1.L = 17., yH3.L = 14.3333 h = 0.1 i 0 xi w1,i w2,i 1.0000000000 17.0000000000 -14.0001920179 1 1.1000000000 15.7554961488 -11.0233385768 2 1.2000000000 14.7733911653 -8.7112939059 3 1.3000000000 13.9977542927 -6.8676175175 4 1.4000000000 13.3886317842 -5.3634064170 5 1.5000000000 12.9167227086 -4.1112334541 6 1.6000000000 12.5600506102 -3.0501060229 7 1.7000000000 12.3018095681 -2.1364242137 8 1.8000000000 12.1289280960 -1.3383516879 9 1.9000000000 12.0310864790 -0.6322028142 10 2.0000000000 12.0000288758 -0.0000610418 11 2.1000000000 12.0290719448 0.5718286786 12 2.2000000000 12.1127474726 1.0941681346 13 2.3000000000 12.2465382236 1.5753844538 14 2.4000000000 12.4266798245 2.0221865406 15 2.5000000000 12.6500101951 2.4399689503 16 2.6000000000 12.9138537239 2.8331091970 17 2.7000000000 13.2159311827 3.2051894605 18 2.8000000000 13.5542889444 3.5591638905 19 2.9000000000 13.9272428451 3.8974862467 20 3.0000000000 14.3333332740 4.2222082675 Tabla de errores. Proyecto Fin de Carrera xi 106 w1,i yHxi L »w1,i - yHxi L» 1.0000000000 17.0000000000 17.0000000000 0.0000000000 1.1000000000 15.7554961488 15.7554545455 0.0000416033 1.2000000000 14.7733911653 14.7733333333 0.0000578320 1.3000000000 13.9977542927 13.9976923077 0.0000619850 1.4000000000 13.3886317842 13.3885714286 0.0000603556 1.5000000000 12.9167227086 12.9166666667 0.0000560420 1.6000000000 12.5600506102 12.5600000000 0.0000506102 1.7000000000 12.3018095681 12.3017647059 0.0000448622 1.8000000000 12.1289280960 12.1288888889 0.0000392071 1.9000000000 12.0310864790 12.0310526316 0.0000338474 2.0000000000 12.0000288758 12.0000000000 0.0000288758 2.1000000000 12.0290719448 12.0290476190 0.0000243257 2.2000000000 12.1127474726 12.1127272727 0.0000201999 2.3000000000 12.2465382236 12.2465217391 0.0000164844 2.4000000000 12.4266798245 12.4266666667 0.0000131579 2.5000000000 12.6500101951 12.6500000000 0.0000101951 2.6000000000 12.9138537239 12.9138461538 7.5700547360µ 10-6 2.7000000000 13.2159311827 13.2159259259 5.2567860820µ 10-6 2.8000000000 13.5542889444 13.5542857143 3.2300976915µ 10-6 2.9000000000 13.9272428451 13.9272413793 1.4657825673µ 10-6 3.0000000000 14.3333332740 14.3333333333 5.9304811728µ 10-8 Método de las diferencias finitas para problemas no lineales. El diseño de esta ventana es muy similar a la del método del disparo lineal, en ella se encuentran también diferentes casillas de texto donde se introducen los parámetros necesarios para la ejecución de este método. En esta ventana se encuentran diferentes casillas de texto donde se introducen los parámetros necesarios para la ejecución de este método.La ecuación debe de ser introducida en la forma y≥ = f HxL y£ , que se indica en la parte superior derecha de la ventana. Existe también otra casilla de texto donde se puede introducir de manera opcional la ecuación real para hacer una comparativa a posteriori del error cometido por el método.A Software para la resolución de EDO 107 continuación existen cuatro casillas de texto donde se introducen el intervalo y los valores de frontera correspondientes a dicho intervalo. Por último el tamaño del paso por el que será dividido el intervalo. En la parte inferior de la ventana se encuentran los botones “Método” y “Salir”. Al hacer clic sobre “Método” se inicia el proceso del cálculo de la aproximación, el cual una vez concluido, mostrará los resultados en la parte izquierda de la ventana, mediante una gráfica donde se representa la solución real y la obtenida y debajo de ésta, en rojo, los puntos de la aproximación. Al hacer clic en “Salir” se cierra la ventana y se vuelve a la ventana principal. A continuación se muestra la ventana y la ejecución en un ejercicio. ô En el ejemplo se toman los siguientes datos: y≥ = 2 y3 donde f HxL = 2 y3 definida en el intervalo @1, 2D con unos valores de frontera f HaL = 1 4 y f HbL = 1 5 y un tamaño de paso de h = 0.25. La ecuación real dada es y = 1 , x +3 la cual se puede ver representada en la gráfica en la parte izquierda de la ventana en azul junto a la representación de la aproximación obtenida en color rojo. Proyecto Fin de Carrera 108 Ventana : M étodo de las disferencias finitas para problemas no lineales. Figura 15 Se obtiene, también, en un fichero aparte los resultados de la ejecución del método. Método del diferencias finitas para el problema no lineal con valor de frontera. y≥ = 2 y3 x œ @1., 2.D, yH1.L = 0.25, yH2.L = 0.2 i xi wi 0 1.0000000000 0.2500000000 1 1.2500000000 0.2353010811 2 1.5000000000 0.2222306398 3 4 1.7500000000 2.0000000000 0.2105320965 0.2000000000 Tabla de errores. h = 0.25 Software para la resolución de EDO xi wi 109 yHxi L »wi - yHxi L» 1.0000000000 0.2500000000 0.2500000000 0. 1.2500000000 0.2353010811 0.2352941176 6.9634618716µ 10-6 1.5000000000 0.2222306398 0.2222222222 8.4175641572µ 10-6 1.7500000000 2.0000000000 0.2105320965 0.2000000000 0.2105263158 5.78067356µ 10-6 0.2000000000 0. Proyecto Fin de Carrera 110 11.3. Métodos de Rayleigh-Ritz Método lineal segmentario de Rayleigh-Ritz. En esta ventana se encuentran diferentes casillas de texto donde se introducen los parámetros necesarios para la ejecución de este método. La ecuación debe de ser introducida en la forma pHxL y≥ + qHxL y = f HxL, que se indica en la parte superior derecha de la ventana. Existe también otra casilla de texto donde se puede introducir de manera opcional la ecuación real para hacer una comparativa a posteriori del error cometido por el método. A continuación existen cuatro casillas de texto donde se introducen el intervalo, que en este método es siempre @0, 1D. Por último el número de subintervalos que se realizan en el intervalo original dado. En la parte inferior de la ventana se encuentran los botones “Método” y “Salir”. Al hacer clic sobre “Método” se inicia el proceso del cálculo de la aproximación, el cual una vez concluido, mostrará los resultados en la parte izquierda de la ventana, mediante una gráfica donde se representa la solución real y la obtenida y debajo de ésta, en rojo, los puntos de la aproximación. Al hacer clic en “Salir” se cierra la ventana y se vuelve a la ventana principal. A continuación se muestra la ventana y la ejecución en un ejercicio. Software para la resolución de EDO ô 111 Se toman los siguientes datos: y≥ + p2 y = 2 p2 senHp xL donde pHxL = 1, qHxL = p2 y f HxL = 2 p2 senHp xL, definida en el intervalo @0, 1D y un número de subintervalos de 9. La ecuación real dada es y = senHp xL, la cual se puede ver representada en la gráfica en la parte izquierda de la ventana en azul junto a la representación de la aproximación obtenida en color rojo. Ventana : Método lineal segmentario de Rayleigh - Ritz. Figura 16 Proyecto Fin de Carrera 112 Se obtiene, también, en un fichero aparte los resultados de la ejecución del método. Método lineal segmentario de Rayleigh - Ritz para aproximar la solución al problema de valor de frontera. „y „ HpHxL L + qHxL y = f HxL „x „x 2 p y- „2 y „ x2 = 2 p2 sinHp xL pHxL = 1 qHxL = p2 f HxL = 2 p2 sinHp xL x œ @0., 1.D, yH0.L = 0, yH1.L = 0 Puntos. n=9 x0 = 0. x1 h1 x2 h2 x3 h3 x4 h4 Hxi , hi L = x5 h5 x6 h6 x7 h7 x8 h8 x9 h9 0.1 0.2 0.3 0.4 = 0.5 0.6 0.1 0.1 0.1 0.1 0.1 0.1 0.7 0.1 0.8 0.1 0.9 0.1 xn+1 = 1. Integrales a evaluar. Q1, i =H 1 hi L2‡ xi+1 xi Hxi+1 -xLHx-xi LqHxL „x 0.164493406685 0.164493406685 0.164493406685 Q1, i = 0.164493406685 0.164493406685 0.164493406685 0.164493406685 0.164493406685 i = 1, 2,..., n-1. Software para la resolución de EDO Q2, i =H 1 hi-1 L2‡ xi xi-1 113 Hx-xi-1 L2 qHxL „x i = 1, 2,..., n. 0.328986813370 0.328986813370 0.328986813370 0.328986813370 Q2, i = 0.328986813370 0.328986813370 0.328986813370 0.328986813370 0.328986813370 Q3, i =H 1 hi L2‡ xi+1 xi Hxi+1 -xL2 qHxL „x i = 1, 2,..., n. 0.328986813370 0.328986813370 0.328986813370 0.328986813370 Q3, i = 0.328986813370 0.328986813370 0.328986813370 0.328986813370 0.328986813370 Q4, i =H Q4, i 1 hi-1 L2‡ xi pHxL„x i = 1, 2,..., n+1. xi-1 10.0000000000 10.0000000000 10.000000000 10.0000000000 10.0000000000 = 10.000000000 10.0000000000 10.0000000000 10.0000000000 10.0000000000 Q5, i = 1 hi-1 ‡ xi xi-1 Hx-xi-1 Lf HxL „x i = 1, 2,..., n. Proyecto Fin de Carrera 114 0.204675558016 0.492161466035 0.731471180669 0.899179399679 Q5, i = 0.978869674097 0.962741364629 0.852373222577 0.658568850666 0.400299171133 Q6, i = 1 hi ‡ xi+1 xi Hxi+1 -xLf HxL „x i = 1, 2,..., n. 0.400299171133 0.658568850666 0.852373222577 0.962741364629 Q6, i = 0.978869674097 0.899179399679 0.731471180669 0.492161466035 0.204675558016 Sistema tridiagonal simétrico: A.x = b. A= 20.658 -9.83551 0 0 0 0 0 0 0 -9.83551 20.658 -9.83551 0 0 0 0 0 0 0 -9.83551 20.658 -9.83551 0 0 0 0 0 0.604975 1.15073 1.58384 1.86192 b = 1.95774 1.86192 1.58384 1.15073 0.604975 0 0 -9.83551 20.658 -9.83551 0 0 0 0 0 0 0 -9.83551 20.658 -9.83551 0 0 0 0 0 0 0 -9.83551 20.658 -9.83551 0 0 0 0 0 0 0 -9.83551 20.658 -9.83551 0 0 0 0 0 0 0 -9.83551 20.658 -9.83551 0 0 0 0 0 0 0 -9.83551 20.658 Software para la resolución de EDO 115 Solución al sistema lineal tridiagonal simétrico. c1 c2 c3 c4 c = c5 c6 c7 c8 c9 0.310286675614 0.590200329525 0.812341063015 0.954964193344 = 1.00410877480 0.954964193344 0.812341063015 0.590200329525 0.310286675614 Tabla de errores en la aproximación. i xi fi Hxi L = ci yHxi L »fHxi L - yHxi L» 1 0.1000000000 0.3102866756 0.3090169944 1.2696812395µ 10-3 2 0.2000000000 0.5902003295 0.5877852523 2.4150772329µ 10-3 3 0.3000000000 0.8123410630 0.8090169944 3.32406864µ 10-3 4 0.4000000000 0.9549641933 0.9510565163 3.9076770484µ 10-3 5 0.5000000000 1.0041087748 1.0000000000 4.1087748009µ 10-3 6 0.6000000000 0.9549641933 0.9510565163 3.9076770483µ 10-3 7 0.7000000000 0.8123410630 0.8090169944 3.32406864µ 10-3 8 0.8000000000 0.5902003295 0.5877852523 2.4150772329µ 10-3 9 0.9000000000 0.3102866756 0.3090169944 1.2696812395µ 10-3 Método de los trazadores cúbicos de Rayleigh - Ritz. En esta ventana se encuentran diferentes casillas de texto donde se introducen los parámetros necesarios para la ejecución de este método. La ecuación debe de ser introducida en la forma pHxL y≥ + qHxL y = f HxL, que se indica en la parte superior derecha de la ventana. Existe también otra casilla de texto donde se puede introducir de manera opcional la ecuación real para hacer una comparativa a posteriori del error cometido por el método. A continuación existen cuatro casillas de texto donde se introducen el intervalo, que Proyecto Fin de Carrera 116 en este método es siempre @0, 1D. Por último el número de subintervalos que se realizan en el intervalo original dado. En la parte inferior de la ventana se encuentran los botones “Método” y “Salir”. Al hacer clic sobre “Método” se inicia el proceso del cálculo de la aproximación, el cual una vez concluido, mostrará los resultados en la parte izquierda de la ventana, mediante una gráfica donde se representa la solución real y la obtenida y debajo de ésta, en rojo, los puntos de la aproximación. Al hacer clic en “Salir” se cierra la ventana y se vuelve a la ventana principal. A continuación se muestra la ventana y la ejecución en un ejercicio. ô Se toman los siguientes datos: -x2 y≥ - 2 x y£ + 2 y = -4 x2 donde pHxL = x2 , qHxL = 2 y f HxL = -4 x2 , definida en el intervalo @0, 1D y un número de subintervalos de 9. La ecuación real dada es y = x2 - x, la cual se puede ver representada en la gráfica en la parte izquierda de la ventana en azul junto a la representación de la aproximación obtenida en color rojo. Software para la resolución de EDO 117 Ventana : Método de los trazadores cúbicos segmentario de Rayleigh - Ritz. Figura 17 Se obtiene, también, en un fichero aparte los resultados de la ejecución del método. Método de trazadores cúbicos de Rayleigh - Ritz para aproximar la solución al problema de valor de frontera. „y „ HpHxL L + qHxL y = f HxL „x „x - „2 y „x 2 x2 - 2 „y „x x + 2 y = -4 x 2 pHxL = x 2 qHxL = 2 f HxL = -4 x 2 x œ @0., 1.D, yH0.L = 0, yH1.L = 0 Proyecto Fin de Carrera 118 Puntos. n=9 x0 = 0. 0 x0 0.1 x1 0.2 x2 0.3 x3 0.4 x4 Hxi L = x5 = 0.5 x6 0.6 x7 0.7 x8 0.8 x9 0.9 x10 1. Tabla de datos para el cálculo de aHi, jL. i j L U k k+h SHai L, SHbi L fi Hx L SHa j L, SHb j L 0 0 0 0.2 0 0.1 1. 1 IH2 - 10. xL3 - 4 H1 - 10. xL3 M - H2 - 10. Hx + 0.1LL3 2. 4 1. 2. 0 0 0 0.2 0.1 0.2 2. 3. H2 - 10. xL3 2. 3. 1 4 0 1 0 0.2 0 0.1 1. 1 IH2 - 10. xL3 - 4 H1 - 10. xL3 M - H2 - 10. Hx + 0.1LL3 2. 4 0 1 0 0.2 0.1 0.2 2. 3. H2 - 10. xL3 1. 3. 0 2 0 0.2 0.1 1. 1 IH2 - 10. xL3 - 4 H1 - 10. xL3 M - H2 - 10. Hx + 0.1LL3 2. 4 -1. 0 0.2 2. 3. 1 H2 - 10. xL3 0. 0 0.2 2. 3. 1 H2 - 10. xL3 -1. 0 0 2 0 0 0.2 0.1 0 3 0.1 0.2 0.1 ai, j = ‡ L U 1 4 4 4 a H0,1L = 0.0861607 a H0,2L = -0.0367857 a H0,3L = -0.00419643 Tabla de datos para el cálculo de bHiL. 4 IH2 - 10. xL3 - 4 H1 - 10. xL3 M - H2 - 10. Hx + 0.1LL3 1 4 H2 - 10. xL3 1 0. 1 IH10. Hx - 0.1L + 2L3 - 4 H10. Hx - 0.1L + 1L3 M - H2 - 10. Hx + 0.1LL3 2. 4 4 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H0,0L = 0.0785714 f j HxL 1 1 4 IH2 - 10. Hx - 0.1LL3 - 4 H1 - 10. Hx - 0.1LL3 M 1 4 1 4 H10. Hx - 0.2L + 2L3 IH10. Hx - 0.2L + 2L3 - 4 H10. Hx - 0.2L + 1L3 M 1 4 H10. Hx - 0.3L + 2L3 Software para la resolución de EDO k k+h SHai L, SHbi L 1. 0 0 0.2 0 0.1 2. 2. 0 0 0.2 0.1 0.2 3. i L 119 fi HxL U bi = ‡ U L 1 4 IH2 - 10. xL3 - 4 H1 - 10. xL3 M - H2 - 10. Hx + 0.1LL3 1 4 H2 - 10. xL3 Hf HxL fi HxLL„x b H0L = -0.000933333 Tabla de datos para el cálculo de aHi, jL. U k k+h SHai L, SHbi L i j L 1 1 0 0.3 1 1 0 0.3 0.1 0.2 0 0.1 1 1 0 0.3 0.2 0.3 1 2 0 0.3 1 2 0 0.3 0.1 0.2 1 2 0 0.3 0.2 0.3 0 0.1 1 3 0.1 0.3 0.1 0.2 1 3 0.1 0.3 0.2 0.3 1 4 0.2 0.3 0.2 0.3 fi HxL SHa j L, SHb j L 1 0. 1 JH10. Hx - 0.1L + 2L3 - 4 H10. Hx - 0.1L + 1L3 N - H2 - 10. Hx + 0.1LL3 2. 4 4 1 1. 3 JH2 - 10. Hx - 0.1LL - 4 H1 - 10. Hx - 0.1LL3 N 3. 4 1 2. H2 - 10. Hx - 0.1LL3 4. 4 1 0. 1 JH10. Hx - 0.1L + 2L3 - 4 H10. Hx - 0.1L + 1L3 N - H2 - 10. Hx + 0.1LL3 2. 4 4 1 1. JH2 - 10. Hx - 0.1LL3 - 4 H1 - 10. Hx - 0.1LL3 N 3. 4 1 2. H2 - 10. Hx - 0.1LL3 4. 4 1 1. JH2 - 10. Hx - 0.1LL3 - 4 H1 - 10. Hx - 0.1LL3 N 3. 4 1 2. H2 - 10. Hx - 0.1LL3 4. 4 1 2. H2 - 10. Hx - 0.1LL3 4. 4 ai, j = ‡ L U f j HxL 1 0. 1 JH10. Hx - 0.1L + 2L3 - 4 H10. Hx - 0.1L + 1L3 N - H2 - 10. Hx + 0.1LL3 2. 4 4 1 1. 3 JH2 - 10. Hx - 0.1LL - 4 H1 - 10. Hx - 0.1LL3 N 3. 4 1 2. H2 - 10. Hx - 0.1LL3 4. 4 1 -1. H10. Hx - 0.2L + 2L3 0 4 1 0. JH10. Hx - 0.2L + 2L3 - 4 H10. Hx - 0.2L + 1L3 N 0 4 1 1. JH2 - 10. Hx - 0.2LL3 - 4 H1 - 10. Hx - 0.2LL3 N 0 4 1 -1. H10. Hx - 0.3L + 2L3 0 4 1 0. JH10. Hx - 0.3L + 2L3 - 4 H10. Hx - 0.3L + 1L3 N 0 4 1 -1. H10. Hx - 0.4L + 2L3 0 4 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H1,1L = 0.445 a H1,2L = 0.06125 a H1,3L = -0.173571 a H1,4L = -0.0116964 Tabla de datos para el cálculo de bHiL. k k+h SHai L, SHbi L 0. 0 0.1 2. 1. 1 0 0.3 0.1 0.2 3. 2. 1 0 0.3 0.2 0.3 4. i L fi HxL U 1 0 0.3 1 4 IH10. Hx - 0.1L + 2L - 4 H10. Hx - 0.1L + 1L M 3 3 1 4 1 4 H2 - 10. Hx + 0.1LL 3 IH2 - 10. Hx - 0.1LL - 4 H1 - 10. Hx - 0.1LL M 3 3 1 4 H2 - 10. Hx - 0.1LL 3 Proyecto Fin de Carrera bi = ‡ U L 120 Hf HxL fi HxLL„x b H1L = -0.00796667 Tabla de datos para el cálculo de aHi, jL. i j L U k k+h SHai L, SHbi L fi Hx L SHa j L, SHb j L -1. 0 1 H10. Hx - 0.2L + 2L3 -1. 0 f j HxL 1 H10. Hx - 0.2L + 2L3 2 2 0 0.4 0 0.1 2 2 0 0.4 0.1 0.2 0. 1 IH10. Hx - 0.2L + 2L3 - 4 H10. Hx - 0.2L + 1L3 M 0 4 0. 1 IH10. Hx - 0.2L + 2L3 - 4 H10. Hx - 0.2L + 1L3 M 0 4 2 2 0 0.4 0.2 0.3 1. 1 IH2 - 10. Hx - 0.2LL3 - 4 H1 - 10. Hx - 0.2LL3 M 0 4 1. 1 IH2 - 10. Hx - 0.2LL3 - 4 H1 - 10. Hx - 0.2LL3 M 0 4 2 2 0 0.4 0.3 0.4 2. 0 H2 - 10. Hx - 0.2LL3 2. 0 1 0.2 0. 1 IH10. Hx - 0.2L + 2L3 - 4 H10. Hx - 0.2L + 1L3 M 0 4 -1. 0 1 2 3 0.1 0.4 0.2 0.3 1. 1 IH2 - 10. Hx - 0.2LL3 - 4 H1 - 10. Hx - 0.2LL3 M 0 4 0. 1 IH10. Hx - 0.3L + 2L3 - 4 H10. Hx - 0.3L + 1L3 M 0 4 2 3 0.1 0.4 0.3 0.4 2. 0 H2 - 10. Hx - 0.2LL3 1. 1 IH2 - 10. Hx - 0.3LL3 - 4 H1 - 10. Hx - 0.3LL3 M 0 4 2 4 0.2 0.4 0.2 0.3 1. 1 IH2 - 10. Hx - 0.2LL3 - 4 H1 - 10. Hx - 0.2LL3 M 0 4 0.4 2. 0 1 0.4 2. 0 1 2 3 0.1 0.4 0.1 2 4 0.2 0.4 0.3 2 5 0.3 0.4 0.3 ai, j = ‡ L U 4 1 4 1 4 4 4 H2 - 10. Hx - 0.2LL3 H2 - 10. Hx - 0.2LL3 -1. 0 4 4 4 1 4 H2 - 10. Hx - 0.2LL3 H10. Hx - 0.3L + 2L3 H10. Hx - 0.4L + 2L3 0. 1 IH10. Hx - 0.4L + 2L3 - 4 H10. Hx - 0.4L + 1L3 M 0 4 -1. 0 1 4 H10. Hx - 0.5L + 2L3 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H2,2L = 0.901429 a H2,3L = -0.0516964 a H2,4L = -0.398571 a H2,5L = -0.0229464 Tabla de datos para el cálculo de bHiL. i L U 2 0 0.4 2 0 0.4 2 0 0.4 2 0 0.4 k k+h SHai L, SHbi L -1. 0 0.1 0 0. 0.1 0.2 0 1. 0.2 0.3 0 2. 0.3 0.4 0 fi HxL 1 4 H10. Hx - 0.2L + 2L3 1 4 IH10. Hx - 0.2L + 2L3 - 4 H10. Hx - 0.2L + 1L3 M 1 4 IH2 - 10. Hx - 0.2LL3 - 4 H1 - 10. Hx - 0.2LL3 M 1 4 H2 - 10. Hx - 0.2LL3 Software para la resolución de EDO bi = ‡ U L 121 Hf HxL fi HxLL„x b H2L = -0.026 Tabla de datos para el cálculo de aHi, jL. i j L U k k+h SHai L, SHbi L fi Hx L SHa j L, SHb j L -1. 0 1 H10. Hx - 0.3L + 2L3 -1. 0 f j HxL 1 H10. Hx - 0.3L + 2L3 3 3 0.1 0.5 0.1 0.2 3 3 0.1 0.5 0.2 0.3 0. 1 IH10. Hx - 0.3L + 2L3 - 4 H10. Hx - 0.3L + 1L3 M 0 4 0. 1 IH10. Hx - 0.3L + 2L3 - 4 H10. Hx - 0.3L + 1L3 M 0 4 3 3 0.1 0.5 0.3 0.4 1. 1 IH2 - 10. Hx - 0.3LL3 - 4 H1 - 10. Hx - 0.3LL3 M 0 4 1. 1 IH2 - 10. Hx - 0.3LL3 - 4 H1 - 10. Hx - 0.3LL3 M 0 4 3 3 0.1 0.5 0.4 0.5 2. 0 H2 - 10. Hx - 0.3LL3 2. 0 1 0.3 0. 1 IH10. Hx - 0.3L + 2L3 - 4 H10. Hx - 0.3L + 1L3 M 0 4 -1. 0 1 3 4 0.2 0.5 0.3 0.4 1. 1 IH2 - 10. Hx - 0.3LL3 - 4 H1 - 10. Hx - 0.3LL3 M 0 4 0. 1 IH10. Hx - 0.4L + 2L3 - 4 H10. Hx - 0.4L + 1L3 M 0 4 3 4 0.2 0.5 0.4 0.5 2. 0 H2 - 10. Hx - 0.3LL3 1. 1 IH2 - 10. Hx - 0.4LL3 - 4 H1 - 10. Hx - 0.4LL3 M 0 4 3 5 0.3 0.5 0.3 0.4 1. 1 IH2 - 10. Hx - 0.3LL3 - 4 H1 - 10. Hx - 0.3LL3 M 0 4 0.5 2. 0 1 0.5 2. 0 1 3 4 0.2 0.5 0.2 3 5 0.3 0.5 0.4 3 6 0.4 0.5 0.4 ai, j = ‡ L U 4 1 4 1 4 4 4 H2 - 10. Hx - 0.3LL3 H2 - 10. Hx - 0.3LL3 -1. 0 4 4 4 1 4 H2 - 10. Hx - 0.3LL3 H10. Hx - 0.4L + 2L3 H10. Hx - 0.5L + 2L3 0. 1 IH10. Hx - 0.5L + 2L3 - 4 H10. Hx - 0.5L + 1L3 M 0 4 -1. 0 1 4 H10. Hx - 0.6L + 2L3 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H3,3L = 1.65143 a H3,4L = -0.220446 a H3,5L = -0.713571 a H3,6L = -0.0379464 Tabla de datos para el cálculo de bHiL. i L U 3 0.1 0.5 3 0.1 0.5 3 0.1 0.5 3 0.1 0.5 k k+h SHai L, SHbi L -1. 0.1 0.2 0 0. 0.2 0.3 0 1. 0.3 0.4 0 2. 0.4 0.5 0 fi HxL 1 4 H10. Hx - 0.3L + 2L3 1 4 IH10. Hx - 0.3L + 2L3 - 4 H10. Hx - 0.3L + 1L3 M 1 4 IH2 - 10. Hx - 0.3LL3 - 4 H1 - 10. Hx - 0.3LL3 M 1 4 H2 - 10. Hx - 0.3LL3 Proyecto Fin de Carrera bi = ‡ U L 122 Hf HxL fi HxLL„x b H3L = -0.056 Tabla de datos para el cálculo de aHi, jL. i j L U k k+h SHai L, SHbi L -1. 0 1 fi Hx L SHa j L, SHb j L H10. Hx - 0.4L + 2L3 -1. 0 f j HxL 1 H10. Hx - 0.4L + 2L3 4 4 0.2 0.6 0.2 0.3 4 4 0.2 0.6 0.3 0.4 0. 1 IH10. Hx - 0.4L + 2L3 - 4 H10. Hx - 0.4L + 1L3 M 0 4 0. 1 IH10. Hx - 0.4L + 2L3 - 4 H10. Hx - 0.4L + 1L3 M 0 4 4 4 0.2 0.6 0.4 0.5 1. 1 IH2 - 10. Hx - 0.4LL3 - 4 H1 - 10. Hx - 0.4LL3 M 0 4 1. 1 IH2 - 10. Hx - 0.4LL3 - 4 H1 - 10. Hx - 0.4LL3 M 0 4 4 4 0.2 0.6 0.5 0.6 2. 0 H2 - 10. Hx - 0.4LL3 2. 0 1 0.4 0. 1 IH10. Hx - 0.4L + 2L3 - 4 H10. Hx - 0.4L + 1L3 M 0 4 -1. 0 1 4 5 0.3 0.6 0.4 0.5 1. 1 IH2 - 10. Hx - 0.4LL3 - 4 H1 - 10. Hx - 0.4LL3 M 0 4 0. 1 IH10. Hx - 0.5L + 2L3 - 4 H10. Hx - 0.5L + 1L3 M 0 4 4 5 0.3 0.6 0.5 0.6 2. 0 H2 - 10. Hx - 0.4LL3 1. 1 IH2 - 10. Hx - 0.5LL3 - 4 H1 - 10. Hx - 0.5LL3 M 0 4 4 6 0.4 0.6 0.4 0.5 1. 1 IH2 - 10. Hx - 0.4LL3 - 4 H1 - 10. Hx - 0.4LL3 M 0 4 0.6 2. 0 1 0.6 2. 0 1 4 5 0.3 0.6 0.3 4 6 0.4 0.6 0.5 4 7 0.5 0.6 0.5 ai, j = ‡ L U 4 1 4 1 4 4 4 4 4 4 -1. 0 1 4 -15 1 3 -1.11022 µ 10 H2 - 10. Hx - 0.4LL H2 - 10. Hx - 0.4LL3 0 4 H2 - 10. Hx - 0.4LL3 H10. Hx - 0.5L + 2L3 H10. Hx - 0.6L + 2L3 IH10. Hx - 0.6L + 2L3 - 4 H10. Hx - 0.6L + 1L3 M -1. 0 1 4 H10. Hx - 0.7L + 2L3 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H4,4L = 2.70143 a H4,5L = -0.445446 a H4,6L = -1.11857 a H4,7L = -0.0566964 Tabla de datos para el cálculo de bHiL. i L U 4 0.2 0.6 4 0.2 0.6 4 0.2 0.6 4 0.2 0.6 k k+h SHai L, SHbi L -1. 0.2 0.3 0 0. 0.3 0.4 0 1. 0.4 0.5 0 2. 0.5 0.6 0 fi HxL 1 4 H10. Hx - 0.4L + 2L3 1 4 IH10. Hx - 0.4L + 2L3 - 4 H10. Hx - 0.4L + 1L3 M 1 4 IH2 - 10. Hx - 0.4LL3 - 4 H1 - 10. Hx - 0.4LL3 M 1 4 H2 - 10. Hx - 0.4LL3 Software para la resolución de EDO bi = ‡ U L 123 Hf HxL fi HxLL„x b H4L = -0.098 Tabla de datos para el cálculo de aHi, jL. i j L U k k+h SHai L, SHbi L -1. 0 1 fi Hx L SHa j L, SHb j L H10. Hx - 0.5L + 2L3 -1. 0 f j HxL 1 H10. Hx - 0.5L + 2L3 5 5 0.3 0.7 0.3 0.4 5 5 0.3 0.7 0.4 0.5 0. 1 IH10. Hx - 0.5L + 2L3 - 4 H10. Hx - 0.5L + 1L3 M 0 4 0. 1 IH10. Hx - 0.5L + 2L3 - 4 H10. Hx - 0.5L + 1L3 M 0 4 5 5 0.3 0.7 0.5 0.6 1. 1 IH2 - 10. Hx - 0.5LL3 - 4 H1 - 10. Hx - 0.5LL3 M 0 4 1. 1 IH2 - 10. Hx - 0.5LL3 - 4 H1 - 10. Hx - 0.5LL3 M 0 4 5 5 0.3 0.7 0.6 0.7 2. 0 H2 - 10. Hx - 0.5LL3 2. 0 1 0.5 0. 1 IH10. Hx - 0.5L + 2L3 - 4 H10. Hx - 0.5L + 1L3 M 0 4 -1. 0 1 5 6 0.4 0.7 0.5 0.6 1. 1 -1.11022 µ 10-15 1 IH2 - 10. Hx - 0.5LL3 - 4 H1 - 10. Hx - 0.5LL3 M IH10. Hx - 0.6L + 2L3 - 4 H10. Hx - 0.6L + 1L3 M 0 4 0 4 5 6 0.4 0.7 0.6 0.7 2. 0 5 7 0.5 0.7 0.5 0.6 1. 1 IH2 - 10. Hx - 0.5LL3 - 4 H1 - 10. Hx - 0.5LL3 M 0 4 5 6 0.4 0.7 0.4 4 1 4 1 4 5 7 0.5 0.7 0.6 0.7 2. 0 1 5 8 0.6 0.7 0.6 0.7 2. 0 1 ai, j = ‡ L U 4 4 H2 - 10. Hx - 0.5LL3 4 4 4 H2 - 10. Hx - 0.5LL3 H10. Hx - 0.6L + 2L3 1. 1 IH2 - 10. Hx - 0.6LL3 - 4 H1 - 10. Hx - 0.6LL3 M 0 4 -1. 0 1 4 -15 1 3 -1.11022 µ 10 H2 - 10. Hx - 0.5LL H2 - 10. Hx - 0.5LL3 0 4 H10. Hx - 0.7L + 2L3 IH10. Hx - 0.7L + 2L3 - 4 H10. Hx - 0.7L + 1L3 M -1. 0 1 4 H10. Hx - 0.8L + 2L3 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H5,5L = 4.05143 a H5,6L = -0.726696 a H5,7L = -1.61357 a H5,8L = -0.0791964 Tabla de datos para el cálculo de bHiL. i L U 5 0.3 0.7 5 0.3 0.7 5 0.3 0.7 5 0.3 0.7 k k+h SHai L, SHbi L -1. 0.3 0.4 0 0. 0.4 0.5 0 1. 0.5 0.6 0 2. 0.6 0.7 0 fi HxL 1 4 H10. Hx - 0.5L + 2L 3 1 4 IH10. Hx - 0.5L + 2L - 4 H10. Hx - 0.5L + 1L M 1 4 IH2 - 10. Hx - 0.5LL - 4 H1 - 10. Hx - 0.5LL M 3 3 3 3 1 4 H2 - 10. Hx - 0.5LL 3 Proyecto Fin de Carrera bi = ‡ U L 124 Hf HxL fi HxLL„x b H5L = -0.152 Tabla de datos para el cálculo de aHi, jL. i j L U SHai L, SHbi L k k+h 6 6 0.4 0.8 0.4 0.5 6 6 0.4 0.8 0.5 0.6 6 6 0.4 0.8 0.6 0.7 6 6 0.4 0.8 0.7 0.8 6 7 0.5 0.8 0.5 0.6 -1. 0 1 4 fi HxL SHa j L, SHb j L H10. Hx - 0.6L + 2L3 -1. 0 1. 1 IH2 - 10. Hx - 0.6LL3 - 4 H1 - 10. Hx - 0.6LL3 M 0 4 0 2. 0 1 IH10. Hx - 0.6L + 2L3 - 4 H10. Hx - 0.6L + 1L3 M -1. 0 1 1 4 4 4 4 -15 1 3 -1.11022 µ 10 1. 1 IH2 - 10. Hx - 0.6LL3 - 4 H1 - 10. Hx - 0.6LL M 0 4 0 6 7 0.5 0.8 0.7 0.8 2. 0 0.7 1. 1 IH2 - 10. Hx - 0.6LL3 - 4 H1 - 10. Hx - 0.6LL3 M 0 4 0.8 2. 0 1 0.8 2. 0 1 6 9 0.7 0.8 0.7 1. 1 IH2 - 10. Hx - 0.6LL3 - 4 H1 - 10. Hx - 0.6LL3 M 0 4 H2 - 10. Hx - 0.6LL3 2. 0 -1.11022 µ 10-15 1 0.7 6 8 0.6 0.8 0.7 4 H10. Hx - 0.6L + 2L3 -1.11022 µ 10-15 1 -1.11022 µ 10-15 1 IH10. Hx - 0.6L + 2L3 - 4 H10. Hx - 0.6L + 1L3 M IH10. Hx - 0.6L + 2L3 - 4 H10. Hx - 0.6L + 1L3 M 0 0 4 4 6 7 0.5 0.8 0.6 6 8 0.6 0.8 0.6 f j HxL 1 ai, j = ‡ L U 1 4 4 4 H2 - 10. Hx - 0.6LL3 H2 - 10. Hx - 0.6LL 3 H2 - 10. Hx - 0.6LL3 4 H2 - 10. Hx - 0.6LL3 H10. Hx - 0.7L + 2L3 IH10. Hx - 0.7L + 2L3 - 4 H10. Hx - 0.7L + 1L3 M 1. 1 IH2 - 10. Hx - 0.7LL3 - 4 H1 - 10. Hx - 0.7LL3 M 0 4 -1. 0 1 4 H10. Hx - 0.8L + 2L3 0. 1 IH10. Hx - 0.8L + 2L3 - 4 H10. Hx - 0.8L + 1L3 M 0 4 -1. -3. 1 4 H10. Hx - 0.9L + 2L3 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H6,6L = 5.70143 a H6,7L = -1.0642 a H6,8L = -2.19857 a H6,9L = -0.105446 Tabla de datos para el cálculo de bHiL. i L U k k+h SHai L, SHbi L -1. 0 6 0.4 0.8 0.4 0.5 6 0.4 0.8 0.5 0.6 -1.11022 µ 10 0 6 0.4 0.8 0.6 0.7 6 0.4 0.8 0.7 0.8 -15 1. 0 2. 0 fi HxL 1 4 H10. Hx - 0.6L + 2L 3 1 4 JH10. Hx - 0.6L + 2L - 4 H10. Hx - 0.6L + 1L N 1 4 JH2 - 10. Hx - 0.6LL - 4 H1 - 10. Hx - 0.6LL N 3 3 3 3 1 4 H2 - 10. Hx - 0.6LL 3 Software para la resolución de EDO bi = ‡ U L 125 Hf HxL fi HxLL„x b H6L = -0.218 Tabla de datos para el cálculo de aHi, jL. i j L U SHai L, SHbi L k k+h -1. 0 1 fi HxL SHa j L, SHb j L H10. Hx - 0.7L + 2L3 -1. 0 f j HxL 1 H10. Hx - 0.7L + 2L3 7 7 0.5 0.9 0.5 0.6 7 7 0.5 0.9 0.6 0.7 7 7 0.5 0.9 0.7 0.8 1. 1 IH2 - 10. Hx - 0.7LL3 - 4 H1 - 10. Hx - 0.7LL3 M 0 4 7 7 0.5 0.9 0.8 0.9 2. 0 H2 - 10. Hx - 0.7LL3 2. 0 1 7 8 0.6 0.9 0.6 0.7 0. 1 IH10. Hx - 0.7L + 2L3 - 4 H10. Hx - 0.7L + 1L3 M 0 4 -1. 0 1 0. 1 IH10. Hx - 0.8L + 2L3 - 4 H10. Hx - 0.8L + 1L3 M 0 4 H2 - 10. Hx - 0.7LL3 1. 1 IH2 - 10. Hx - 0.8LL3 - 4 H1 - 10. Hx - 0.8LL3 M 0 4 4 1 4 7 8 0.6 0.9 0.7 0.8 1. 1 IH2 - 10. Hx - 0.7LL3 - 4 H1 - 10. Hx - 0.7LL3 M 0 4 7 8 0.6 0.9 0.8 0.9 2. 0 7 9 0.7 0.9 0.7 0.8 1. 1 IH2 - 10. Hx - 0.7LL3 - 4 H1 - 10. Hx - 0.7LL3 M 0 4 7 9 0.7 0.9 0.8 0.9 2. 0 1 0.9 2. 0 1 7 10 0.8 0.9 0.8 4 -1.11022 µ 10-15 1 -1.11022 µ 10-15 1 IH10. Hx - 0.7L + 2L3 - 4 H10. Hx - 0.7L + 1L3 M IH10. Hx - 0.7L + 2L3 - 4 H10. Hx - 0.7L + 1L3 M 0 0 4 4 ai, j = ‡ L U 1 4 4 4 1. 1 IH2 - 10. Hx - 0.7LL3 - 4 H1 - 10. Hx - 0.7LL3 M 0 4 4 4 -1. -3. 1 4 H2 - 10. Hx - 0.7LL3 H10. Hx - 0.8L + 2L3 H10. Hx - 0.9L + 2L3 H2 - 10. Hx - 0.7LL3 0. 1 IH10. Hx - 0.9L + 2L3 - 4 H10. Hx - 0.9L + 1L3 M -2. 4 H2 - 10. Hx - 0.7LL3 -1. -2. 1 4 H10. Hx - 1.L + 2L3 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H7,7L = 7.65143 a H7,8L = -1.45795 a H7,9L = -2.87357 a H7,10L = -0.135446 Tabla de datos para el cálculo de bHiL. i L U k k+h SHai L, SHbi L -1. 0 7 0.5 0.9 0.5 0.6 7 0.5 0.9 0.6 0.7 -1.11022 µ 10 0 7 0.5 0.9 0.7 0.8 7 0.5 0.9 0.8 0.9 -15 1. 0 2. 0 fi HxL 1 4 H10. Hx - 0.7L + 2L 3 1 4 JH10. Hx - 0.7L + 2L - 4 H10. Hx - 0.7L + 1L N 1 4 JH2 - 10. Hx - 0.7LL - 4 H1 - 10. Hx - 0.7LL N 3 3 3 3 1 4 H2 - 10. Hx - 0.7LL 3 Proyecto Fin de Carrera U bi = ‡ L 126 Hf HxL fi HxLL„x b H7L = -0.296 Tabla de datos para el cálculo de aHi, jL. i j L U k k+h SHai L, SHbi L f j HxL -1. 0 0.8 0. 1 IH10. Hx - 0.8L + 2L3 - 4 H10. Hx - 0.8L + 1L3 M 0 4 0. 0 1 8 0.6 1. 0.8 0.9 1. 1 IH2 - 10. Hx - 0.8LL3 - 4 H1 - 10. Hx - 0.8LL3 M 0 4 1. 0 1 8 0.6 1. 0.9 1. 8 0.6 1. 0.6 0.7 8 8 0.6 1. 0.7 8 8 8 fi Hx L SHa j L, SHb j L H10. Hx - 0.8L + 2L3 8 9 0.7 1. 0.7 -1. 0 1 4 1 4 4 4 IH10. Hx - 0.8L + 2L3 - 4 H10. Hx - 0.8L + 1L3 M IH2 - 10. Hx - 0.8LL3 - 4 H1 - 10. Hx - 0.8LL3 M H2 - 10. Hx - 0.8LL3 2. 0 1 0.8 0. 1 IH10. Hx - 0.8L + 2L3 - 4 H10. Hx - 0.8L + 1L3 M 0 4 -1. -3. 1 1. 1 IH2 - 10. Hx - 0.8LL3 - 4 H1 - 10. Hx - 0.8LL3 M 0 4 0. -2. 8 9 0.7 1. 0.8 0.9 8 9 0.7 1. 0.9 1. 8 10 0.8 1. 0.8 0.9 8 10 0.8 1. 0.9 2. 0 1 4 2. 0 1 4 -1. -2. H2 - 10. Hx - 0.8LL3 0. -1. ai, j = ‡ L U 1 4 4 4 H2 - 10. Hx - 0.8LL3 H10. Hx - 0.9L + 2L3 IH10. Hx - 0.9L + 2L - 4 H10. Hx - 0.9L + 1L3 M 3 1 1. 1 IH2 - 10. Hx - 0.9LL3 - 4 H1 - 10. Hx - 0.9LL3 M - H10. Hx - 1.1L + 2L3 -1. 4 4 1. 1 IH2 - 10. Hx - 0.8LL3 - 4 H1 - 10. Hx - 0.8LL3 M 0 4 2. 0 1. H2 - 10. Hx - 0.8LL3 4 1 H10. Hx - 0.8L + 2L3 1 4 1 4 H10. Hx - 1.L + 2L3 IH10. Hx - 1.L + 2L3 - 4 H10. Hx - 1.L + 1L3 M - H10. Hx - 1.1L + 2L3 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H8,8L = 9.90143 a H8,9L = -1.73875 a H8,10L = -2.96179 Tabla de datos para el cálculo de bHiL. i L U 8 0.6 1. 8 0.6 1. 8 0.6 1. 8 0.6 1. k k+h SHai L, SHbi L -1. 0.6 0.7 0 0. 0.7 0.8 0 1. 0.8 0.9 0 2. 0.9 1. 0 bi = ‡ L U Hf HxL fi HxLL„x fi HxL 1 4 H10. Hx - 0.8L + 2L3 1 4 IH10. Hx - 0.8L + 2L3 - 4 H10. Hx - 0.8L + 1L3 M 1 4 IH2 - 10. Hx - 0.8LL3 - 4 H1 - 10. Hx - 0.8LL3 M 1 4 H2 - 10. Hx - 0.8LL3 Software para la resolución de EDO 127 b H8L = -0.386 Tabla de datos para el cálculo de aHi, jL. j 9 0.7 1 0.7 0.8 -1. -3. 9 9 0.7 1 0.8 0.9 0. -2. 9 L U k k+h SHai L, SHbi L i 9 9 0.7 1 0.9 H10. Hx - 0.9L + 2L3 -1. -3. JH10. Hx - 0.9L + 2L3 - 4 H10. Hx - 0.9L + 1L3 N 0. -2. 4 1 4 1 1 1. JH2 - 10. Hx - 0.9LL3 - 4 H1 - 10. Hx - 0.9LL3 N - H10. Hx - 1.1L + 2L3 -1. 4 4 1 0. JH10. Hx - 0.9L + 2L3 - 4 H10. Hx - 0.9L + 1L3 N -2. 4 1 1 1. JH2 - 10. Hx - 0.9LL3 - 4 H1 - 10. Hx - 0.9LL3 N - H10. Hx - 1.1L + 2L3 -1. 4 4 1. 9 10 0.8 1 0.8 0.9 9 10 0.8 1 0.9 fi HxL SHa j L, SHb j L 1 1. U ai, j = ‡ L f j HxL 1 4 1 4 H10. Hx - 0.9L + 2L3 JH10. Hx - 0.9L + 2L3 - 4 H10. Hx - 0.9L + 1L3 N 1 1 1. JH2 - 10. Hx - 0.9LL3 - 4 H1 - 10. Hx - 0.9LL3 N - H10. Hx - 1.1L + 2L3 -1. 4 4 1 -1. H10. Hx - 1.L + 2L3 -2. 4 1 0. JH10. Hx - 1.L + 2L3 - 4 H10. Hx - 1.L + 1L3 N - H10. Hx - 1.1L + 2L3 -1. 4 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x a H9,9L = 16.645 a H9,10L = 7.82991 Tabla de datos para el cálculo de bHiL. k k+h SHai L, SHbi L -1. 9 0.7 1 0.7 0.8 -3. 0. 9 0.7 1 0.8 0.9 -2. 1. 9 0.7 1 0.9 1. -1. i fi HxL L U bi = ‡ U L 1 4 1 4 1 4 H10. Hx - 0.9L + 2L 3 IH10. Hx - 0.9L + 2L - 4 H10. Hx - 0.9L + 1L M 3 IH2 - 10. Hx - 0.9LL - 4 H1 - 10. Hx - 0.9LL M 3 3 3 1 4 H10. Hx - 1.1L + 2L 3 Hf HxL fi HxLL„x b H9L = -0.437967 Tabla de datos para el cálculo de aHi, jL. i j L U k k+h SHai L, SHbi L 10 10 0.8 1 0.8 0.9 10 10 0.8 1 0.9 1. -1. -2. fi HxL SHa j L, SHb j L 1 4 H10. Hx - 1.L + 2L3 0. 1 IH10. Hx - 1.L + 2L3 - 4 H10. Hx - 1.L + 1L3 M - H10. Hx - 1.1L + 2L3 -1. 4 ai, j = ‡ L U -1. -2. f j HxL 1 4 H10. Hx - 1.L + 2L3 0. 1 IH10. Hx - 1.L + 2L3 - 4 H10. Hx - 1.L + 1L3 M - H10. Hx - 1.1L + 2L3 -1. 4 HpHxL fi £ HxL f j £ HxL+qHxL fi HxL f j HxLL„x Proyecto Fin de Carrera 128 a H10,10L = 14.1786 Tabla de datos para el cálculo de bHiL. k k+h SHai L, SHbi L -1. 10 0.8 1 0.8 0.9 -2. 0. 10 0.8 1 0.9 1. -1. i fi HxL L U bi = ‡ U L 1 4 1 4 H10. Hx - 1.L + 2L 3 IH10. Hx - 1.L + 2L - 4 H10. Hx - 1.L + 1L M - H10. Hx - 1.1L + 2L 3 3 3 Hf HxL fi HxLL„x b H10L = -0.176933 Sistema con una matriz simétrica en banda: A.x = b. A= 0.0785714 0.0861607 -0.0367857 -0.00419643 0 0 0 0 0 0 0.0861607 0.445 0.06125 -0.173571 -0.0116964 0 0 0 0 0 0 -0.0367857 0.06125 0.901429 -0.0516964 -0.398571 -0.0229464 0 0 0 0 0 -0.00419643 -0.173571 -0.0516964 1.65143 0 -0.0116964 -0.398571 -0.220446 0 0 -0.0229464 -0.713571 0 0 0 -0.0379464 0 -0.220446 -0.713571 -0.0379464 0 0 0 0 2.70143 -0.445446 -1.11857 -0.0566964 0 0 0 -0.445446 4.05143 -0.726696 -1.61357 -0.0791964 0 0 -1.11857 -0.726696 5.70143 -1.0642 -2.19857 -1.0642 7.65143 -1.45795 -2.87357 -0.135446 -1.45795 9.90143 -1.73875 -2.96179 0 0 0 0 -0.0566964 -1.61357 0 0 0 0 0 -0.0791964 -2.19857 -0.105446 0 0 0 0 0 0 0 -0.105446 -2.87357 -1.73875 16.645 7.82991 0 0 0 0 0 0 0 -0.135446 -2.96179 7.82991 14.1786 -0.000933333 -0.00796667 -0.026 -0.056 -0.098 b = -0.152 -0.218 -0.296 -0.386 -0.437967 -0.176933 Solución al sistema lineal simétrico. Se aplica el método de Cholesky. La matriz A es definida positiva. Software para la resolución de EDO c0 c1 c2 c3 c4 c = c5 c6 c7 c8 c9 c10 -0.00222222222147 -0.0622222222237 -0.108888888890 -0.142222222226 -0.162222222225 = -0.168888888894 -0.162222222225 -0.142222222224 -0.108888888891 -0.0622222222165 -0.00222222223236 0 -0.0933333333355 -0.163333333335 -0.213333333339 -0.243333333338 f Hxi L = -0.253333333341 -0.243333333337 -0.213333333336 -0.163333333336 -0.0933333333247 -7.77156120782µ 10-18 129 Proyecto Fin de Carrera 130 n+1 f HxL = ‚ ci HxL fi HxL = i=0 -0.00222222 4 H10. Hx - 1.1L + 1L3 - H10. Hx - 1.1L + 2L3 + 1 4 1 4 1 4 1 4 1 4 1 4 1 4 1 4 1 4 1 4 IH2 - 10. Hx - 1.LL3 - 4 H1 - 10. Hx - 1.LL3 M + -0.0622222 IH2 - 10. Hx - 0.9LL3 - 4 H1 - 10. Hx - 0.9LL3 M - 1 4 H10. Hx - 1.1L + 2L3 + -0.108889 IH2 - 10. Hx - 0.8LL3 - 4 H1 - 10. Hx - 0.8LL3 M + -0.142222 IH2 - 10. Hx - 0.7LL - 4 H1 - 10. Hx - 0.7LL M + 3 3 -0.162222 IH2 - 10. Hx - 0.6LL3 - 4 H1 - 10. Hx - 0.6LL3 M + -0.168889 IH2 - 10. Hx - 0.5LL - 4 H1 - 10. Hx - 0.5LL M + 3 3 -0.162222 IH2 - 10. Hx - 0.4LL3 - 4 H1 - 10. Hx - 0.4LL3 M + -0.142222 IH2 - 10. Hx - 0.3LL3 - 4 H1 - 10. Hx - 0.3LL3 M + -0.108889 IH2 - 10. Hx - 0.2LL3 - 4 H1 - 10. Hx - 0.2LL3 M + -0.0622222 IH2 - 10. Hx - 0.1LL3 - 4 H1 - 10. Hx - 0.1LL3 M + -0.00222222 1 4 IH2 - 10. xL3 - 4 H1 - 10. xL3 M - H2 - 10. Hx + 0.1LL3 Tabla de errores en la aproximación con el método. i 0 1 2 3 4 5 6 7 8 9 10 xi ci 0 -0.0022222222 0.1 -0.0622222222 0.2 -0.1088888889 0.3 -0.1422222222 0.4 -0.1622222222 0.5 -0.1688888889 0.6 -0.1622222222 0.7 -0.1422222222 0.8 -0.1088888889 0.9 -0.0622222222 1. -0.0022222222 fHxi L 0.0000000000 -0.0900000000 -0.1600000000 -0.2100000000 -0.2400000000 -0.2500000000 -0.2400000000 -0.2100000000 -0.1600000000 -0.0900000000 0.0000000000 yHxi L 0.0000000000 -0.0900000000 -0.1600000000 -0.2100000000 -0.2400000000 -0.2500000000 -0.2400000000 -0.2100000000 -0.1600000000 -0.0900000000 0.0000000000 »fHxi L - yHxi L» 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. Software para la resolución de EDO 131 11.4. Menú Ayuda Ayuda al usuario. Al ejecutar esta opción del menú se abre un fichero de Mathematica con una descripción de cada uno de los métodos implementados en la aplicación que sirve de ayuda a la ejecución de los mismos. El usuario puede ir desplegando cada uno de los métodos donde, aparte de una descripción, encontrará el pseudocódigo de dicho método. Ventana : Ayuda al usuario. Figura 18 Proyecto Fin de Carrera 132 Acerca de la aplicación. Al ejecutar esta opción aparece esta ventana con toda la información relevante del programa. Ventana : Acerca de la aplicación Figura 19 Software para la resolución de EDO 133 12. Valoración económica y planificación 12.1. Valoración económica del proyecto En este apartado se detalla la valoración económica de cada una de las actividades que comprenden la realización y puesta en funcionamiento del presente proyecto. Las diferentes partidas o ítems que componen el proyecto y que se han incluido en este análisis de costes se detallan a continuación. 1. Especificaciones y Desarrollo Software Esta partida o ítem se ha dividido en dos grandes fases debido a su gran alcance e importancia. En primer lugar, aparece la fase de requisitos. Esta fase incluye las fases de especificación de requisitos, del análisis funcional y del plan de pruebas. Y en segundo lugar, se indica la fase de desarrollo del software. Esta fase es sin duda la que ha supuesto más coste, en términos de tiempo, y la que distingue el presupuesto del de otro proyecto que comprenda el mismo ámbito o sea del mismo tipo. En esta fase se indican los diferentes métodos de aproximacion programados y probados. Para cada una de las fases anteriores se reseñan los costes directos, expresados en meses/hombre (meses completos dedicados para cada actividad), necesarios para acometer Proyecto Fin de Carrera 134 cada una de ellas, indicándose la categoría del realizador: Jefe de Proyecto o Analista/Programador. La actividad del Jefe de Proyecto se ha estimado en un 14% respecto de la actividad del Analista/Programador. Por último, cabe destacar que no debe haber confusión con el significado de los costes unitarios aquí expresados. Estos costes representan la valoración económica real que determinaría la empresa por la realización completa de todas las actividades reseñadas y poner a cargo de este proyecto a dicho Jefe de Proyecto o Analistas en su caso. 2. Instalación, Pruebas e Integración del Software En este apartado se recogen los costes directos de las actividades de integración y de pruebas del software en el entorno de desarrollo y en el de explotación, incluidos los gastos adicionales, tales como los desplazamientos y las dietas. Estos costes han sido calculados del mismo modo que en el apartado anterior. 3. Equipamiento y Licencias Software Costes de todo el equipamiento e infraestructura (PCs, impresoras, RAL, comunicaciones), si fuera necesario. Así mismo, se han de especificar en este apartado las licencias necesarias para el entorno de explotación. Para la implementación de este software sólo es necesario una licencia del lenguaje numérico y simbólico de Mathematica®, en concreto de la versión 6.0 aquí utilizada, y disponer de un PC. Como la venta de este software será con toda seguridad a una persona Software para la resolución de EDO 135 jurídica no se contempla en este presupuesto la adquisición de dicha plataforma hardware, debido a que en los tiempos presentes cualquier empresa o persona jurídica dispone de un PC, haciéndose sólo referencia a la licencia del Mathematica®. 4. Apoyo logístico (Formación) En este concepto se ampara la formación a impartir a los posibles operadores y administradores del sistema a implantar. Se incluye en la formación la entrega de toda la documentación necesaria para el curso de formación. 5. Incrementos e IVA Se parte de la suma de las partidas (1), (2), (3), y (4) formando el Coste Directo del Proyecto. A este Coste Directo se le aplican los Gastos Generales H13 %L y el Beneficio Industrial H6 %L. La suma de los conceptos de Coste Directo, Gastos Generales y Beneficio Industrial constituyen el Total Importe sin IVA. A este importe se le sumarán los impuestos correspondientes como IVA H16 %L, para la Península y Baleares, IGIC H5 %L para las islas Canarias o IPSI para Ceuta H3 %L y Melilla H4 %L. Total Proyecto La suma del Total Importe sin IVA más la partida de Incrementos e IVA determinan el importe total del desarrollo, implantación y puesta en servicio del proyecto. Proyecto Fin de Carrera 136 En función de lo explicado anteriormente se puede proceder a calcular los costes estimados del presente proyecto. El importe total del proyecto asciende a 24.176, 04 € (VEINTICUATRO MIL CIENTO SETENTA Y SEIS EUROS CON CUATRO CÉNTIMOS), impuestos incluidos. Software para la resolución de EDO El detalle de cada una de las partidas reseñadas se expresa en la tabla siguente: 137 Proyecto Fin de Carrera 138 12.2. Planificación temporal del proyecto En el diagrama de Gantt de actividades siguiente se reflejan las tareas e hitos más importantes para el desarrollo y ejecución de este Proyecto Fin de Carrera, así como la planificación temporal final dedicada a cada uno de ellas. Planificación temporal del Proyecto. Figura 20 Software para la resolución de EDO 139 13. Conclusiones Una vez realizado el presente proyecto fin de carrera sobre el estudio, programación y aplicación de diferentes métodos numéricos para la resolución de ecuaciones diferenciales ordinarias de segundo orden con valor en frontera se pueden expresar las siguientes conclusiones al mismo. 1.- La aproximación a la solución mediante el método del disparo lineal que utiliza el método de Runge-Kutta de cuarto orden, ofrece una precisión o exactitud OIh4 M. Tiene el inconveniente de que utiliza una técnica por error en el redondeo que puede, en algún caso, presentar algún problema oculto, pudiendo ofrecer una pérdida de los dígitos significativos debido al proceso de cancelación en el algoritmo empleado, es decir, pérdida de significación al restar dos cantidades próximas entre sí. Tiene la ventaja de que ha sido un método relativamente fácil de implementar en el lenguaje de programación Mathematica. 2.- El método del disparo no lineal, también emplea el método Runge-Kutta de cuarto orden para aproximar la solución pero ha exigido el empleo del método de Newton para la resolución de una ecuación no lineal. La aplicación de estos métodos implica que el problema de valor inicial se resuelva de una manera aproximada y no exacta. También se podría haber utilizado en este algoritmo el método de la Secante para la resolución de la ecuación no lineal que aparece, si bien el método empleado, el de Newton, ofrece una mayor rapidez de convergencia. Reseñar que el método del disparo para problemas no lineales es vulnerable a los errores de redondeo, singularmente si las soluciones y HxL y z Hx, tL fueran funciones que crecieran muy rápidamente en el intervalo Proyecto Fin de Carrera 140 @a, bD. 3.- Los métodos de diferencias finitas, para problemas lineales y no lineales, presentan mejores características de estabilidad, a costa de realizar más cómputo para obtener la solución con la misma precisión. Estos métodos de diferencias finitas reemplazan las derivadas en la ecuación diferencial por un cociente de diferencias centradas, lo que obliga a escoger un parámetro h, tamaño del subintervalo, no demasiado pequeño. En particular, el método de las diferencias finitas para problemas lineales emplea la resolución de un sistema lineal tridiagonal, cuya solución única requiere que cumpla el teorema ya explicitado en el método. Este método presenta un error del orden OIh2 M frente al error de truncamiento OIh4 M que incluía el método de Runge-Kutta. 4.- En el método de las diferencias finitas para problemas no lineales aparece un sistema de ecuaciones no lineal, lo que ha exigido un método numérico iterativo: el método de Newton para sistemas de ecuaciones no lineales. Esto implica que en cada paso de la iteración se tiene que resolver de N µ N y se tiene que emplear el concepto de la matriz Jacobiana. Este método es del orden de convergencia OIh2 M. 5.- Se ha abordado el problema con valor en frontera para la resolución de ecuaciones diferenciales en el método de Rayleigh-Ritz, primero, reformulando el problema seleccionando del conjunto de todas las funciones suficientemente derivables aquellas que reducen al mínimo una determinada integral. Y en segundo lugar, se reduce el tamaño de funciones candidatas para dar una aproximación al problema. El método emplea un pequeño conjunto de funciones que son combinaciones lineales de ciertas funciones básicas, ello da origen a la resolución de un sistema lineal formado por una matriz Software para la resolución de EDO 141 simétrica, en el que cada elemento se obtiene mediante la integración en el intervalo @0, 1D de una combinación de las funciones que intervienen en la ecuación diferencial y las funciones básicas y sus derivadas. Una elección de las funciones básicas es la selección de polinomios lineales definidos por tramos (método lineal segmentario de Rayleigh-Ritz). Y otra elección la utilización de funciones básicas formadas por trazadores cúbicos definidos por intervalos linealmente independientes (método de los trazadores cúbicos de Rayleigh-Ritz). La dificultad práctica de este método es la evaluación de las integrales, que se pueden hacer mediante fórmulas de cuadratura o mediante su evaluación directa. En el presente proyecto se ha utilizado la técnica de evaluación directa con Mathematica. En el método lineal segmentario se ha resuelto el sistema tridiagonal simétrico mediante el método de eliminación de Gauss, mientras que en el método de los trazadores cúbicos, al aparecer una matriz simétrica definida positiva se ha empleado el método de Cholesky. La evaluación de las integrales en el método de los trazadores cúbicos, se ha realizado mediante la evaluación directa con las funciones de Mathematica, lo que ha producido una mayor aproximación de las integrales. Este método es especialmente recomendable cuando el problema con valor de frontera se define en el intervalo [0, 1]. 6.- Habiendo estudiado e implementado los métodos reseñados anteriormente se establece como líneas futuras de trabajo o mejoras a incluir en este proyecto fin de carrera Proyecto Fin de Carrera 142 las que a continuación se indican: a) En el método de las diferencias para problemas lineales se podría mejorar la precisión empleando la serie de Taylor de quinto orden para aproximar y≥ Hxi L e y£ Hxi L, pero el sistema lineal resultante no sería tridiagonal, lo que requeriría un mayor esfuerzo computacional para su resolución. También se podría utilizar para mejorar la precisión el método de extrapolación de Richardson para los dos métodos de las diferencias finitas. b) En el método de Rayleigh-Ritz, los trazadores cúbicos (trazadores B) se podrían definir con una base formada por polinomios cúbicos definidos por intervalos de Hermite. c) Otra técnica que podría complementar los anteriores métodos sería el método de colocación: este procedimiento selecciona un conjunto de funciones básicas, 8f1 , ..., fn < y un conjunto de puntos 8x1 , …, xn < definidos en el intervalo @0, 1D tomando estos puntos como los nodos de las raíces de polinomios ortogonales. Software para la resolución de EDO 143 Anexo I. Manual de Instalación y de Usuario Manual de Instalación Para poder instalar el software Mathematica es necesario disponer de entre 900 y 1.200 MB libres de disco duro, 1 GB de memoria RAM y una unidad de CD-ROM. La versión de Mathematica que se va a instalar es la version 6.0. Para instalarla simplemente hay que ejecutar el fichero setup.exe que se encuentra en el CD. Para la correcta visión y ejecución del proyecto es necesario instalar unas plantillas. Las plantillas de Mathematica se copian en el directorio donde se haya instalado el Software de Resolución de Problemas con valor en frontera para la Resolución de Ecuuaciones Diferenciales Ordinarias en el mismo directorio. D:\Software EDO\ Las plantillas básicas a emplear en el PFC son cuatro: a) Proyecto_Fin_de_Carrera.nb: plantilla a emplear con el fichero PFC. b) Proyecto_Fin_de_Carrera(Resumen).nb: plantilla que se usará con el fichero PFC (Nombre y Apellidos) (Resumen, Abstact, Índice).nb. c) Proyecto_Fin_de_Carrera (Sin código).nb. Se empleará con el fichero PFC cuando tenga los problemas incluidos. d) Código_Métodos_Numéricos_12.nb (Ficheros de Problemas y de los Proyecto Fin de Carrera 144 Algoritmos Numéricos). También es necesario instalar un paquete especial para poder visualizar y utilizar la interfaz de usuario. El paquete de Mathematica The Super Widget Package (SWP) se ha diseñado para crear interfaces de usuario (GUI) con Mathematica. Se necesita el fichero superwidgetpackage.zip V. 4.52 compatible con Mathematica 5.2 o versiones superiores. La instalación de Super Widget Package (Versión 4.52 libre) se realiza del modo siguiente: 1. Se copia el fichero superwidgetpackage.zip en el directorio indicado en el directorio $BaseDirectory, ejecutado en Mathematica. Ejemplo: 2. "C:\ProgramData\\Mathematica" Se debe preservar la estructura de ficheros contenida en el fichero ZIP. Se descomprime el fichero pero preservando la estructura de ficheros. 3. Se inicia Mathematica, y en menú Help se selecciona Rebuild Help index. Para integrar la documentación de SWP con el resto de Mathematica. 4. La ayuda de este paquete, Super Widget Package (SWP), se encuentra en Help Browser y en la solapa Add-ons & Links. Software para la resolución de EDO 145 Manual de Usuario Para utilizar la aplicación es necesario tener instalado el software Mathematica 6.0, el paquete The Super Widget y las plantillas suministradas en el CD. a) Se debe abrir y ejecutar todo el fichero "Código (Problemas de Contorno con Ecuaciones Diferenciales Ordinarias).nb". Para ejecutar todo el fichero se debe seleccionar en la barra de herramientas de Mathematica "Kernel", "Evaluation" y "Evaluate Notebook". Así serán reconocidos todos los algoritmos desarrollados. b) Se ejecuta el archivo denominado "Interfaz.nb". Para resolver problemas con esta interfaz se siguen los siguientes pasos: 1. Seleccionar el método del menú principal. 2. Introducir los datos necesarios para la resolución del problema como se indica en la ventana del método. 3. Pulsar el botón "Método". Una vez que se han obtenido los resultados si que quiere volver a resolver un problema con el mismo método volver a introducir los datos en la misma ventana y pulsar el botón "Método". Si se quiere resolver un problema con otro método o salir de la aplicación se debe cerrar la ventana del método y se vuelve a la ventana principal de la aplicación desde la que se puede cerrar la aplicación o ejecutar problemas con cualquier método siguiendo los pasos anteriores. Proyecto Fin de Carrera 146 Bibliografía [BURD98] Burden, Richard. L.; Faires, J. Douglas. Análisis Numérico. 6º Edición. International Thomson Editores, México, 1998. [CARN79] Carnahan, Brice; Luther, H. A.; Wilkes, James O. Cálculo Numérico. Métodos, Aplicaciones. Editorial Rueda, Madrid, 1979. [CHAP87] Chapra, Steven C.; Canale, Raymond P. Métodos Numéricos para Ingenieros con aplicaciones en Computadora. McGraw-Hill. México, 1987. [FINS96] Finschi, Lucas. An Implementation of the Levenberg-Marquardt. Algorithm. Zürich, 1996. [GERA00] Gerald, F. ; Wheatley, Patrick O. Análisis Numérico con Aplicaciones. Pearson Educación, México, 2000. Software para la resolución de EDO [LAMP96] 147 Lampton, Michael. Damping–undamping strategies for the Levenberg–Marquardt. University of California, Berkeley, California. Octubre 1996. [MATH00] Mathews, John H.; Fink, Kurtis D. Métodos Numéricos con MATLAB. 3ª edición. Prentice Hall, Madrid, 2000. [MORE99] Moreno González, Carlos. Cálculo Numérico II. 1ª Edición. Ed. UNED. Madrid, 1999. [RINC01] Rincón, F. Análisis Matemático y Métodos Numéricos para Informática Ed. Dpto. Publicaciones de la E.U.I. Madrid, 2001. [RODR03] Rodríguez Gómez, Fco. Javier Cálculo y Métodos Numéricos. Teoría, Algoritmos y Problemas Resueltos UPCO. Madrid, 2003. [ZILL06] Zill, Dennis G.; Cullen, Michael R. Ecuaciones diferenciales con problemas de valores en la frontera. 6ª Edición. Proyecto Fin de Carrera International Thomson Editores, México, 2006. URL’s [1] http://sai.azc.uam.mx/apoyodidactico/ Métodos Numéricos. [2] http://www.library.cornell.edu/nr/ Libro Numerical Recipes in C. 148