Teoría Electromagnética, R.S. Murphy. Capítulo 3, ejercicio 3.2

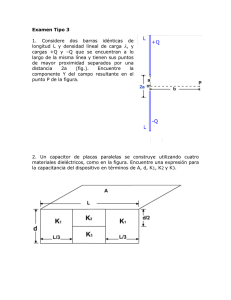
Teoría Electromagnética, R.S. Murphy. Capítulo 3, ejercicio 3.2, página 117.
Una esfera conductora de radio a se rodea con un cascarón concéntrico de
radio b, y el sistema se mantiene a una diferencia de potencial constante igual
a V = V0 . Con la ecuación de Laplace:
a) Encuentra el potencial para la región entre la esfera y el cascarón
b) Calcula el campo eléctrico en todo punto
c) Determina las densidades de carga, asi como la carga total, en la esfera y
en el cascarón.
Solución:
La solución general de la ecuación de Laplace en coordenadas esféricas para
problemas con simetría azimutal (es decir, que no dependan del ángulo '), es
1
X
Bn
V (r; ) =
An rn + n+1 Pn (cos )
r
n=0
Primero debemos de imponer la condición que
V (r = a; ) = Va
donde Va es el potencial al cual se coloca la esfera interior.
La condición queda
1
X
Bn
V (r = a; ) =
An an + n+1 Pn (cos ) = Va
a
n=0
de donde es claro que
B0
A0 +
= Va
a
o bien
B0 = a (Va A0 )
y además
An = 0
Bn = 0
para toda n > 0:
Por lo tanto, la solución la tenemos por ahora como
a
V (r; ) = A0 + (Va A0 )
r
Imponemos ahora la la condición de que el potencial de la segunda esfera,
la exterior, sea constante, digamos Vb ;
a
V (r = b) = A0 + (Va A0 ) = Vb
b
de donde es evidente que
aVa bVb
A0 =
a b
Sustituyendo en la expresión que ya teníamos para el potencial
aVa bVb
aVa bVb a
aVa bVb
Va V b 1
V (r; ) =
+ Va
=
ab
a b
a b
r
a b
a b r
Finalmente
ab
1
aVa bVb
(Va Vb )
V (r; ) =
a b
a b
r
Para comprobación podemos evaluar sobre cada una de las super…cies
aVa bVb
ab
1
V (r = a; ) =
(Va Vb ) = Va
a b
a b
a
1
aVa bVb
ab
1
(Va Vb ) = Vb
a b
a b
b
y ver que da lo que se exige en el problema.
Es muy fácil, además, veri…car que de verdad es una solución de la ecuación
de Laplace
!
aVa bVb
ab
1
2
=0
r
(Va Vb ) p
a b
a b
x2 + y 2 + z 2
Dado que la solución a la ecuación de Laplace, con condiciones a la frontera
…jas, es única, pues ésta es.
V (r = b; ) =
2