n - Unet

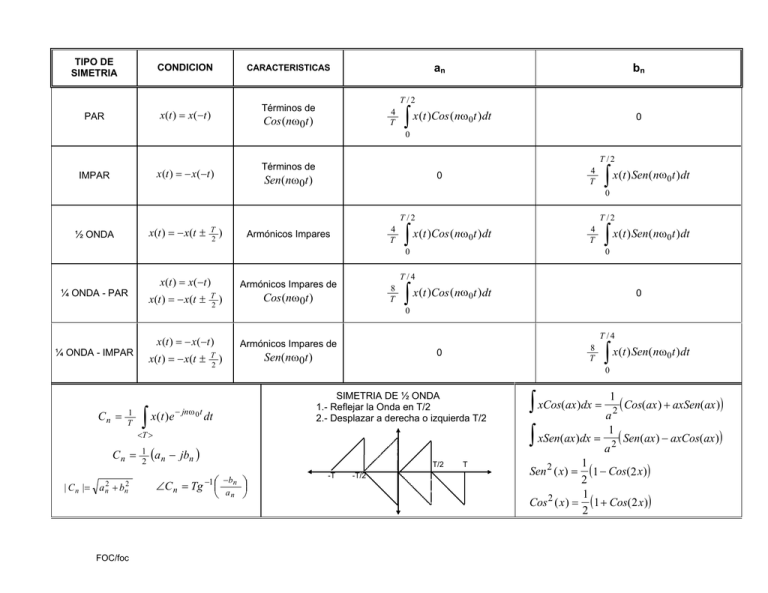
TIPO DE
SIMETRIA
PAR
CONDICION
CARACTERISTICAS
x ( t ) = x ( −t )
Términos de
an
bn
T /2
4
T
Cos (nω0t )
∫ x(t )Cos (nω t )dt
0
0
0
x (t ) = − x(−t )
IMPAR
T /2
Términos de
4
T
0
Sen(nω0t )
∫ x(t ) Sen(nω t )dt
0
0
T /2
x (t ) = − x (t ±
½ ONDA
T
2
)
4
T
Armónicos Impares
T /2
∫ x(t )Cos (nω t )dt
4
T
0
0
x ( t ) = x ( −t )
¼ ONDA - PAR
x (t ) = − x (t ±
T
2
Cn =
1
T
x (t ) = − x (t ±
∫ x (t )e
− jnω 0 t
T
2
8
T
Cos (nω0t )
∫ x(t )Cos (nω t )dt
| C n |= a n2 + bn2
FOC/foc
1
2
0
0
T /4
Armónicos Impares de
0
Sen(nω0t )
)
8
T
SIMETRIA DE ½ ONDA
1.- Reflejar la Onda en T/2
2.- Desplazar a derecha o izquierda T/2
dt
(a n − jbn )
∠C n = Tg −1 

∫ x(t ) Sen(nω t )dt
0
0
<T >
Cn =
0
0
x (t ) = − x(−t )
¼ ONDA - IMPAR
0
T /4
Armónicos Impares de
)
∫ x(t ) Sen(nω t )dt
T/2
−bn
an


-T
-T/2
T
∫ xCos(ax)dx = a12 ( Cos(ax) + axSen(ax))
∫ xSen(ax)dx = a12 ( Sen(ax) − axCos(ax))
1
( 1 − Cos(2 x))
2
1
Cos 2 ( x ) = ( 1 + Cos(2 x ))
2
Sen 2 ( x ) =
Tabla 1.- PROPIEDADES DE LA SERIE CONTINUA DE FOURIER.
Propiedad
Señal Periódica
Coeficientes de la Serie de
Fourier
x(t )  Periódicas con período T y

2π
y (t ) frecuencia fundamental ω0 = T
Cx k
Linealidad
Ax(t) + By(t)
ACx k + BCy k
Desplazamiento en
tiempo
x(t – t0)
Cx k e
Desplazamiento en
frecuencia
e
Conjugación
x*(t)
Cx *− k
Inversión en tiempo
x(-t)
Cx − k
Escalamiento en tiempo
X(at), a>0 (periódica con período T/a)
Cx k
Convolución periódica
∫T x(τ) y(t − τ)dτ
TCx k Cy k
Multiplicación
x(t)y(t)
jMω0t
x(t ) = e
jM 2 π t
T x (t )
Cy k
− jkω0t0
= Cx k e
− jk 2π t0
T
Cx k − M
∞
∑ Cxl Cy k −l
l = −∞
Diferenciación
dx(t )
dt
t
Integración
∫ x(t )dt
−∞
(de valor finito y periódica
solo si a0 = 0)
jkω0 Cx k = jk
2 π Cx
k
T
Cx k =
Cx k
1
jkω0
1
jk 2π
T
Simetría conjugada
para señales reales
x(t) real
Cx = Cx *
−k
 k

Re Cx k = Re Cx − k

Im Cx k = − Im Cx − k

 Cx = Cx
−k
 k

∠Cx k = −∠Cx −k
Señal real y par
x(t) real y par
Cxk real y par
Señal real e impar
x(t) real e impar
Cxk solo imaginario e impar
Descomposición par e
impar de señales reales
x(t)=xp(t) + xi(t) [x(t) real]
xp(t)= Componente par de x(t)
xi(t)= Componente impar de x(t)
Re|Cxk|
jIm|Cxk|
Relación de Parseval para señales periódicas
∫
1
|
T T
x(t ) | 2 dt =
∞
∑ | Cxk |2
k = −∞
Tabla 2.- PROPIEDADES DE LA TRANSFORMADA DE FOURIER.
Propiedad
Señal Aperiódica
Transformada de Fourier
x (t )
X (ω)
y (t )
Y (ω)
Linealidad
ax(t) + by(t)
aX (ω) + bY (ω)
Desplazamiento en
tiempo
x(t – t0)
e
Desplazamiento en
frecuencia
e
Conjugación
x*(t)
X * (−ω)
Inversión en tiempo
x(-t)
X (− ω)
Escalamiento en tiempo
x(at)
1
a
Convolución
x(t ) * y( t)
X (ω) ⋅ Y (ω)
Multiplicación
x(t)y(t)
1
2π
Diferenciación
dx(t )
dt
− jωt0
X (ω − ω 0 )
jω0t
x (t )
∫ x(t )dt
1
jω
−∞
Diferenciación en
frecuencia
X ( ωa )
X (ω) ∗ Y (ω)
jωX (ω)
t
Integración
X (ω)
X (ω) + πX (0)δ(ω)
t x(t)
j ddω X (ω)
Simetría conjugada
para señales reales
x(t) real
 X (ω) = X ∗ (−ω)

Re X (ω) = Re X (−ω)


Im X (ω) = − Im X (−ω)

 X (ω) = X (−ω)

∠ X (ω) = −∠ X (−ω)

Señal real y par
x(t) real y par
X (ω) real y par
Señal real e impar
x(t) real e impar
X (ω) solo imaginario e
impar
Descomposición par e
impar de señales reales
x(t)=xp(t) + xi(t) [x(t) real]
xp(t)= Componente par de x(t)
xi(t)= Componente impar de x(t)
Re| X (ω) |
jIm| X (ω) |
Relación de Parseval para señales aperiódicas
∞
∫ | x(t ) |
−∞
2
dt =
∞
1
2π
∫ | X (ω) |
−∞
2
dω
Tabla 3.- PARES BÁSICOS DE LA TRANSFORMADA DE FOURIER.
Señal
∞
∑ Ck e
jk ω0t
Transformada
e
∞
∑ C k δ (ω − kω0 )
2π
k =−∞
k =−∞
Ck
C1 = 1
2πδ (ω − ω0 )
jω0t
Coeficientes de la Serie de Fourier
(si es periódica)
Ck = 0 ; k ≠ 1
cos (ω 0t )
π [δ (ω − ω 0 ) + δ (ω + ω 0 )]
sen (ω0 t )
π [δ (ω − ω ) − δ (ω + ω )]
0
0
j
C1 = C −1 =
1
2
C k = 0 ; otro valor de k
C1 = −C −1 =
1
2j
C k = 0 ; otro valor de k
C0 = 1
2πδ (ω)
x(t) = 1
Ck = 0 ; k ≠ 0
(para cualquier T > 0)
Onda cuadrada periódica
| t |< T1
1
x (t ) = 
T1 <| t |≤ T2
0
y
∞
2 sen ( kω0T1 )
δ (ω − kω 0 )
k
k =−∞
∑
ω0T1
π
sinc

kω0T1 
π 

=
sen ( kω0T1)
kπ
x(t + T )= x(t)
∞
∑ δ (t − nT )
2π
T
n = −∞
1
x (t ) = 
0
| t |< T1
| t |> T1
∞
∑ δ (ω − 2Tπk )
k = −∞
2 sen ( ωT1 )
ω
sen (W t )
πt
1
X (ω) = 
0
δ (t )
1
u (t )
Ck =
| ω |< W
| ω |> W
-
1
jω
+ πδ (ω)
-
δ (t − t 0 )
e
e − at u (t ) ; Re(a) > 0
1
a + jω
-
te − at u (t ) ; Re(a) > 0
1
( a + jω) 2
-
t n−1 e −at u (t ) ; Re(a) > 0
( n−1)!
1
( a + jω) n
-
− jωt0
-
1
T
para todo k