Exámenes de Ingeniería Técnica Industrial. Mecánica VII
Anuncio

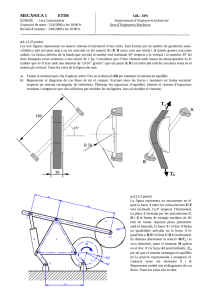
MECÀNICA 1 ETIM UdG - EPS Departament d’Enginyeria Mecànica i Construcció Industrial Àrea d’Enginyeria Mecànica. 01/06/2001 1era Convocatòria Exposició de notes : 07/06/2001 a les 18:00 h. Revisió d’examen : 11/06/2001 a les 10:00 h. a.1. (2 punts) La figura mostra la comporta d’un dipòsit i el seu sistema d’accionament. La comporta està formada per una planxa rectangular inclinada 45º i tres nervis. La comporta té una amplada total de 800 mm. Els nervis són triangles rectangles on cada catet té una longitud de 240 mm. La separació entre cada nervi és de 150 mm i el nervi central coincideix amb la secció central de la comporta. Els nervis estan units fermament a l’eix articulat en els coixinets A i B. La transmissió entre l’eix de la comporta i l’eix paral·lel (articulat en C i D) es fa mitjançant un parell de rodes dentades, 1 i 2. 1 2 B D A C Mides i Distàncies: Longitud total de l’eix AB 750 mm Longitud total de l’eix CD 350 mm ∅ primitiu roda 1 400 mm ∅ primitiu roda 2 200 mm Angle de pressió 20º Distància entre A i B 200 mm Distància entre C i D 200 mm Distància de B a la roda 150 mm Distància de D a la roda 150 mm Determinar: a) La posició del centre de gravetat de la comporta respecte el seu eix de gir. Considerar que està formada per una peça rectangular i tres triangles rectangles. La densitat superficial d’aquestes peces és de 40·10-3 gr/mm2. b) Moment que s’ha d’aplicar al voltant de l’eix C-D per aconseguir que el sistema estigui en equilibri. Les úniques forces que s’han de tenir en compte són el pes de la pròpia comporta i les resultants de la pressió del fluid contra la comporta (el pes específic del fluid és 1·103 kp/m3). c) Reaccions en els coixinets C i D quan el sistema està en equilibri. F a.2. (1,5 punts) En el mecanisme de la figura el pes del cilindre homogeni de radi 20 mm és P = 75 N. La longitud L és de 50 mm i la força F sempre és en la direcció de la barra BC. La longitud natural del ressort correspon a la posició en que θ = 60º i la seva constant elàstica és K = 5 N/mm. P L L C L L A Es demana calcular pel mètode del treball virtual el valor de la força F corresponent a la posició d’equilibri en que θ = 45º. θ B MECÀNICA 1 ETIM UdG - EPS Departament d’Enginyeria Mecànica i Construcció Industrial Àrea d’Enginyeria Mecànica. 01/06/2001 1era Convocatòria Exposició de notes : 07/06/2001 a les 18:00 h. Revisió d’examen : 11/06/2001 a les 10:00 h. b.1. (2 punts) La figura representa un sistema d'elevació de petits paquets on l’única massa a considerar és la del paquet homogeni, W, de 25 kp. Els braços CE i GH romanen sempre paral·lels, fent que la plataforma de càrrega, FG, sempre es trobi en posició horitzontal. Sobre el braç EC s’hi ha practicat una guia, horitzontal, en la posició representada, per on llisca el pern D on s’articulen el cilindre hidràulic AD i la barra BD. Es demana determinar la força feta pel cilindre hidràulic per mantenir l’equilibri del sistema en la posició representada, les reaccions en el pern D i forces sobre la plataforma FG. W G F H D E A C B b.2. (2 punts) Sobre una superfície horitzontal hi ha el cilindre 1, de pes menystenible, format per dos tambors solidaris de radis R2 = 240 mm i R1 = 160 mm, i el bloc 2, de pes 500 N, on L = 120 mm. Entorn del tambor de radi R1 passa una cinta en un extrem de la qual penja el pes W = 100 N i de l’altre s’estira amb la força horitzontal F. Només es considera fregament en les superfícies cilindre-terra, tambor-cinta i bloc-terra, on el coeficient de fricció és 0.2 en tots els casos. Es demana calcular la màxima força F que garanteix l’equilibri del sistema. F 1 2 W MECÀNICA 1 ETIM UdG - EPS Departament d’Enginyeria Mecànica i Construcció Industrial Àrea d’Enginyeria Mecànica. 01/06/2001 1era Convocatòria Exposició de notes : 07/06/2001 a les 18:00 h. Revisió d’examen : 11/06/2001 a les 10:00 h. b.3. (1,5 punts) En el muntatge de la figura la cinta està subjectada en un dels seus extrems a l’estructura de barres articulades mitjançant un dinamòmetre i en l’altre se li aplica un pes P. Aquesta cinta passa entorn del tambor 1, de radi r1 = 30 cm, fixat a la bancada i de la politja 2, de radi r2 = 10 cm, que pot girar lliurement a través de l’articulació A, situada a una distància R = 45 cm del centre del tambor. La barra G disposa d’un sistema per mesurar la deformació unitària que indica ε = -14µε, mentre el dinamòmetre marca el valor de tracció F. Es demana: a) La força que pateix la barra G tenint en compte que totes les barres són d’alumini (E = 71000 MPa) de secció 10·10·2 mm. Indicar si la barra està sotmesa a tracció o a compressió. b) Calcular, segons el mètode dels nusos, la força que mesura el dinamòmetre (la longitud de totes les barres horitzontals i verticals és L). c) Pes P que cal aplicar perquè la politja 2 rodi en sentit antihorari si el coeficient de fregament entre tambor i cinta val µ = 0.24. F 5 1 L L 3 4 A G l 2 L L L 2 P R