Exámenes de Ingeniería Técnica Industrial. Mecánica VIII
Anuncio

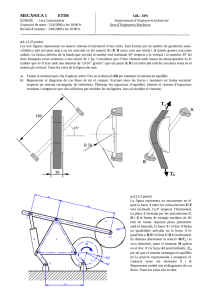
MECÀNICA 1 ETIM UdG - EPS Departament d’Enginyeria Mecànica i Construcció Industrial Àrea d’Enginyeria Mecànica. 26/06/2001 2ona Convocatòria Exposició de notes: 02/07/2001 a les 18:00 h. Revisió d’examen: 04/07/2001 a les 15:00 h. a.1. (2,5 punts) La figura mostra una locomotora de ferrocarril. La parella de rodes davanteres rep un moment motriu produït per la caldera de vapor. Aquesta parella de rodes està connectada a les rodes posteriors mitjançant una biela sempre paral·lela a la via (mostrada a la figura), això permet que les rodes posteriors també actuïn com a rodes motrius. La locomotora té una massa de 5 tones i el coeficient de frec entre les rodes i els rails és 0.3. a) Determinar la màxima força, paral·lela a la via, aplicada en el punt d’ancoratge dels vagons abans de que comencin a lliscar les rodes si la pendent és nul·la (α = 0). Calcular les reaccions de cada parell de rodes amb la via. b) Calcular, pel cas anterior, el moment motriu i força sobre la biela (quan la biela està en la seva posició més baixa, tal com mostra la figura) c) Si no hi han vagons enganxats, quina és el màxim pendent (α màxim) que pot ascendir la locomotora abans de que comencin a lliscar les rodes o a bolcar la locomotora? punt d’ancoratge dels vagons α biela 2 E B K 3 1 4 θ A a.2. (2 punts) La figura representa un mecanisme en el qual els elements 1 i 2, units a través de la barra 3 de longitud 4R, estan formats per un tambor de radi R = 25 mm solidari a un engranatge de radi 2R. La barra 4, entre les articulacions A i B, també de longitud 4R, està inclinada un angle θ respecte la vertical. El ressort elàstic, de constant K = 5 N/mm, s’enrotlla entorn dels tambors de 1 i 2 de manera que la seva longitud natural coincideix amb la posició determinada per θ = 0º. C D Si les úniques forces exteriors a considerar són els pesos dels elements 1 i 2, de 1600 N cadascun, es demana calcular el valor de l’angle θ que determina la posició d’equilibri. MECÀNICA 1 ETIM 26/06/2001 2ona Convocatòria Exposició de notes: 02/07/2001 a les 18:00 h. Revisió d’examen: 04/07/2001 a les 15:00 h. UdG - EPS Departament d’Enginyeria Mecànica i Construcció Industrial Àrea d’Enginyeria Mecànica. b.1. (2 punts) El mecanisme de la figura representa un sistema mecànic sense fregaments. Està format bàsicament per tres cossos. La politja 1 de radi 180 mm que està articulada respecte el seu centre. La politja 2, també de radi 180 mm, es pot desplaçar verticalment. El seguidor 3 només es pot moure horitzontalment. Els vuit passadors representats a la figura fan de sistema de guiatge d’aquests moviments. El seguidor en un extrem està en contacte amb la politja 2, l’angle d’inclinació del pla de contacte respecte la vertical és de 15º. En l’altre extrem està en contacte amb una molla de constant de rigidesa k = 12 N/mm. En la posició que mostra la figura la molla està distesa. F 2 3 a) Determinar el valor de T per aconseguir que la politja 2 s’elevi 90 mm, sabent que la força F val 100 N. 1 b) Trobar en aquest cas quant valen les reaccions en els passadors que guien el moviment de la lleva 2 i del seguidor 3. T b.2. (2 punts) Tenim un element resistent d’una estructura de secció transversal tal i com mostra la figura (a), formada per dos quarts de cercle de radi R = 4 cm. Es vol reduir el seu pes fent dos orificis a l’element de manera que la secció quedarà travessada per dos forats amb forma de cercle de radi r = 1 cm (veure figura b). a) Determinar en quina posició d on han de quedar els dos forats si volem que la nova secció redueixi la seva inèrcia centroidal respecte l’eix horitzontal un 25% b) Determinar la posició i orientació dels eixos centroidals principals de la secció (figura b) si d valgués 2 cm. figura (a) figura (b) MECÀNICA 1 ETIM 26/06/2001 2ona Convocatòria Exposició de notes: 02/07/2001 a les 18:00 h. Revisió d’examen: 04/07/2001 a les 15:00 h. UdG - EPS Departament d’Enginyeria Mecànica i Construcció Industrial Àrea d’Enginyeria Mecànica. b.3. (1,5 punts) El mecanisme de la figura representa una balança. Els punts D i E són articulacions fixes dels dos sectors mostrats. Els sectors estan en contacte de manera que no existeix lliscament relatiu entre ells. Es parteix de la posició indicada i es penja un pes de 7 kg de massa al punt C de l’estructura de barres biarticulades, fent girar el sistema un angle α. Si el contrapès té una massa P = 3 kg , l’angle β = 75º i la barra AC = 120 mm, es demana calcular: a) Forces que actuen sobre els passadors A i B. b) L’angle α girat per l’agulla c) La deformació unitària de la barra BC si les barres són d’alumini (E = 71000 MPa) i de secció A = 64 mm2. Les unitats de la figura són en mm. E D β A B C