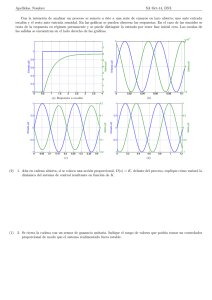
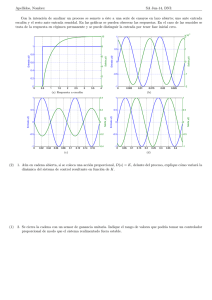
Diseño de Sistema de Control para UAV * Curso: Sistemas de Control Automático, Universidad de Costa Rica 1st Luis Sergio Yannicelli Vargas, A87086 2nd José López Picado, B43869 3rd Rodrigo Villalta Chaves, B57859 Universidad de Costa Rica Estudiante de Fı́sica e Ingenierı́a Eléctrica San José, Costa Rica lsyannicelli@gmail.com Universidad de Costa Rica Estudiante de Ingenierı́a Eléctrica San José, Costa Rica joselp1695@gmaill.com Resumen—En este artı́culo se identifica un modelo de altura para un UAV a partir de la curva de reacción del proceso ante una entrada escalón, cuya entrada es el ángulo del elevador. A patir del modelo obtenido se sintonizan varios controladores de la familia PID para lograr una efectiva acción de control tanto en servo control como en control regulatorio. Index Terms—UAV, PID, MATLAB. Luego de obtener de ecuaciones de movimiento y asumiendo que la masa y el momento de inercia del UAV es constante se obtiene el siguiente modelo: P (s) = I-A. I. I NTRODUCCI ÓN En la actualidad, ha aumentado el desarrollo de los vehı́culos aéreos no tripulados (UAV, de sus siglas en inglés). Especı́ficamente en el área militar, debido a los riesgos que conlleva involucrar vidas humanas en misiones de alto riesgo. Además, todo los inconvenientes que pueden traer el desempeño de un mal piloto, clima, lugar, entre otros. Debido a los avances tecnológicos se pueden recrear simulaciones bastantes precisas del modelo, ayudando a los costos del proyecto. La implementación de un controlador que lleve a cabo esta tarea debe ser un proceso minucioso y detallado [1]. Por lo que se procede a generar una serie de ecuaciones a partir de la siguiente imagen. Universidad de Costa Rica Estudiante de Ingenierı́a Eléctrica San José, Costa Rica rodrigovch5@gmail.com −57,3(s − 24,6) s3 + 1,82s2 + 0,8281s (2) Normalización de señales Para efectos de este documento se toma como altura máxima de vuelo 20m, la altura estándar máxima para UAV’s de baja altitud [1]. Por otro lado la señal de control pude variar ±0,07145rad o en grados ±10o [1]. La señal de control, realimentada y referencia estarán normalizadas con respecto a estos valores tope. El punto de operación del UAV es de 10m, altura para la que obtenido el modelo lineal de la ecuación 2, según el articulo suministrado como ayuda [1]. II. I DENTIFICACI ÓN DEL MODELO Para poder implementar un proceso de diseño del controlador se asume el modelo como una caja negra. En esta consideración lo que se toma en cuenta es únicamente la información de la entrada y salida del proceso. Por lo que se debe realizar una identificación del mejor modelo que describa el proceso para el sistema de control realimentado y luego proceder a diseñar el controlador. Al excitar el proceso con un escalón unitario de magnitud unitaria se obtiene la curva de reacción de la figura 2. Como se observa en dicha figura, la planta tiene un comportamiento integrante de orden dos o más, sin aparente respuesta inversa y con una ganancia elevada. Figura 1. Designación de los parámetros del UAV [1]. Las variables de interés son la altura en metros y el ángulo de inclinación de la proa del UAV en radianes. De forma que se tiene: H(s) P (s) = Θ(s) (1) Para la identificación se utiliza dos aproximaciones, una integrante de orden uno mas tiempo muerto (MIPOMT) y otra integrante de segundo orden mas tiempo muerto (MISOMT), esto debido a que como limitante el controlador tiene que ser de la familia PID y un orden mayor en la planta dificultarı́a en proceso de sintonización. Para la identificación del modelo se utilizó un script en MatLab que realiza una aproximación por ası́ntotas. Con este resultado se obtuvieron aproximaciones iniciales de los esto se puede solucionar garantizando al menos un mı́nimo de robustez. Por todo lo anterior el modelo escogido para la sintonización es el MISOMT, ya que de los modelos de segundo orden es el que mejor se ajusta. Curva de reacción de la planta ante un escalón de magnitud unitaria 3500 3000 2500 y [m] 2000 1500 1000 Respuesta de la planta y los modelos al escalón unitario 1400 500 1200 0 1000 -500 0 2 4 6 8 10 12 14 16 18 20 800 Figura 2. Curva de reacción de la planta ante un escalón de magnitud unitaria. y [m] tiempo [s] 600 Planta MIPOMT MISOMT MISO 400 200 parámetros de los 3 modelos obtenidos, luego se procedio a variarlos hasta obtener un mejor ajuste en cada modelo. 0 -200 0 1 2 3 4 5 6 7 8 9 10 tiempo [s] II-A. MIPOMT Figura 3. Respuesta de la planta y los modelos al escalón unitario. −LS P (s) = Parámetro K L Ke s (3) Modelo 1708,05e−2,27s s 1708,05e−0,59s s(1,69s+1) 1708,05 s(2,29s+1) Valor 1708.05 2.24 IAE ITAE ISE 2336.61 7916.15 1260075.73 252.72 1361.58 1885.44 7920.95 Cuadro I 7030.16 498163.59 I NDICADORES OBTENIDOS PARA LOS MODELOS IDENTIFICADOS . II-B. MISOMT P (s) = Ke−LS s(T s + 1) Parámetro K L T II-C. III. S INTONIZACI ÓN DEL CONTROLADOR Valor 1708.05 0.69 1.69 MISO P (s) = K s(T s + 1) Parámetro K T II-D. (4) (5) Valor 1708.05 2.29 Comparación de los modelos obtenidos Al someter los modelos a una entrada escalón unitario, se obtiene el comportamiento dinámico de la figura 3. Tal y como se esperaba, los modelos de segundo orden captura mejor la dinámica del proceso real, ya que contiene más información del mismo. Por otro lado, al analizar los ı́ndices de error de la tabla I el resultado es el mismo, los modelos de segundo orden resulta mejor para modelar la dinámica del UVA. Aún ası́ debido a la alta ganancia de la planta y a la naturaleza integrante y a la complejidad que podrı́a acarrear un modelo más exacto, no se logra disminuir más los ı́ndices de error. Sin embargo Figura 4. Esquema de control. El esquema de control general para controlar la altura del UAV se presenta en la figura 4. En este caso la perturbación no afecta a la planta alterando la posición angular del elevador, si no más bien se manifiesta alterando directamente la altura del vehı́culo no tripulado, debido a un descenso en la presión o al efecto del viento. Por otro lado para efectos de este documento el controlador C(s) es un controlador PID de uno o dos GdL, según corresponda. Realizando la sustitución del controlador por una de dos GdL, se puede llegar a la siguiente función de transferencia: y(s) = Cr (s)P (s) 1 r(s) + d(s) 1 + Cy (s)P (s) 1 + Cy (s)P (s) (6) Para el caso de un controlador de un gdl se cumple que: Cr (s) = Cy (s) (7) Por otro lado P(s) es el modelo MISOMT obtenido de la identificación. En este caso el LGR del mismo se muestra en la figura 5. En donde se observa con claridad un polo en aproximadamente s = −0,581 y otro en el origen lo que le da la caracterı́stica integrante. LGR planta identificada con Tune 0.4 0.3 Imaginary Axis (seconds -1 ) 0.2 0.1 0 Tiempo de asentamiento al dos por ciento menor a 10 segundos. Error permanente cero. Y para servo control: Sobrepaso máximo cercano a cero. Error permanente cero. Es posible descartar controladores tipo P y PD, debido a que ante entradas en perturbación de tipo rampa el error permanente no es igual a cero. Además se desea cancelar el polo de la planta, por lo que el algoritmo de control que mejor se adapta es el PID. -0.1 -0.2 III-B. -0.3 -0.4 -0.6 -0.5 -0.4 -0.3 Real Axis (seconds -0.2 -1 -0.1 0 0.1 ) Figura 5. LGR del modelo de la planta. En cuanto a la acción del controlador, para esta planta será inversa, porque si el ángulo de la proa del avión sube, la altura aumenta; si el ángulo proa baja la altura baja. Por lo tanto : accion = +1 III-A. (8) Especificaciones del lazo de control Los UAV, como todo vehı́culo aéreo, están expuestos a la imprevisibilidad de la atmósfera terrestre. De hecho los aviones comerciales poseen sistemas de control que ayudan a mitigar los efectos que tienen los cambios en velocidad, dirección y la densidad del aire. Cabe destacar, que los cambios de velocidad del aire pueden ser lineales, es decir, en una misma dirección, por lo que pueden ser modelados como una rampa. Además, aparecen ”bolsas de aire”que son espacios donde no hay aire, entonces el avión experimenta una pequeña caı́da debido a que pierde fuerza de sustentación debido a la ausencia de fluido; esto se puede modelar como un escalón. También se debe considerar la turbulencia, que consiste en la formación de vórtices de aire, que tiene un movimiento rotacional y estocástico. Este tipo de perturbación no la hemos tomado en cuenta en las simulaciones, debido a su complejidad en su modelado. Por esta razón se desea una rápida acción de control ante cambios en las perturbaciones. Además se desea que esta respuesta sea suave, del tipo crı́ticamente amortiguada, ya que oscilaciones en la respuesta pueden ocasionar que el UAV se desplome. Además recordando del proceso de modelado las discrepancias entre el modelo y la planta, es necesario garantizar un mı́nimo de robustez, por lo cual el M s debe ser de al menos 2. En resumen, para control regulatorio se desea: Sobrepaso máximo cercano a cero. Diseño I Se ha utilizado la herramienta Tune de Simulink de Matlab para poder sintonizar de forma automática el modelo obtenido anteriormente durante la identificación. Para esto, se ha construido el diagrama de bloques clásico realimentado de lazo cerrado. Para el controlador se utiliza el bloque PID, en el cual se ha utilizado el PID clásico de un grado de libertad. Con la herramienta tune se logra encontrar los parámetros del sistema. Esta herramienta despliega una respuesta estimada, donde se pueden modificar manualmente los parámetros de la curva. Ası́ se manipularon los parámetros hasta conseguir una respuesta suave y subamortiguada. Luego, se verifica este resultado con la salida del lazo cerrado y después de unas cuantas iteraciones se encontró la siguiente respuesta en la figura 6: Los parámetros hallados son los siguientes (tabla III-B): Parámetros diseño 1 Kp 0.0004581 Ti 0.0573040 s Td 1.2826271 s N 10 Cuadro II PAR ÁMETROS OBTENIDOS PARA DISE ÑO 1 CON HERRAMIENTA T UNE DE M ATLAB La herramienta tune, según MathWorks [2], realiza una aproximación rápida de los parámetros del controlador para que sea robusto y con un tiempo de respuesta deseado. Este tiempo es posible realizarlo de forma manual. Primero, la herramienta identifica la planta y la linealiza inyectando unos valores de prueba, recogiendo valores de entrada y salida para distintas frecuencias, estimando ası́ una ganancia DC, proponiendo un controlador inicial. Después realiza la estabilización del sistema con múltiples iteraciones y permite al usuario hacer el ajuste lineal. Con esto es posible exportar los datos al entorno. En la imagen 6 se puede observar como el el sistema se estabiliza rápidamente. Se obtuvo una respuesta subamortiguada. Tarda aproximadamente unos 30 s. Posteriormente, se aplica una perturbación en 70 s en forma de escalón, como se mencionó en la primera sección, 85 2 r(t):escalón d(t):escalón d(t):rampa 80 0 70 -1 e [m] 60 -2 55 -3 50 -4 45 -5 40 -6 60 70 80 90 100 110 120 tiempo [s] -7 50 60 70 80 90 100 110 120 tiempo [s] Figura 6. Respuesta de la señal realimentada con perturbación y ante cambios a la entrada. es cuando el UAV se encuentra con una bolsa de aire y en el caso de la rampa, es un cambio en la velocidad del viento. Ante estas perturbaciones tarda aproximadamente unos 25 s en estabilizarse. Además, se hace un cambio en la referencia y de igual forma, controlador es capaz de estabilizar la señal rápidamente. Con respecto a la acción de control se obtuvo el siguiente resultado: Figura 8. Señal de error ante perturbación de rampa, escalón y cambio de referencia. 1 Fragilidad para planta sintonizada con Tune L(j ) M S=1.2 0.5 M S=2.0 -1 0 L(j ) L(j ) y% 65 35 50 r(t):escalón d(t):escalón d(t):rampa 1 75 -0.5 -1 -1.5 -2 -1.5 -1 -0.5 0 0.5 L(j ) Figura 9. Diagrama de Nyquist para verificar fragilidad para diseño 1. r(t):escalón d(t):escalón d(t):rampa 5 0 una salida que se regula rápidamente y suavemente y es no frágil. Es capaz de resistir cambios en los parámetros de su controlador. u% -5 -10 -15 Para su desempeño se han medido los siguientes parámetros a partir de la curva: -20 50 60 70 80 90 100 110 120 tiempo [s] Figura 7. Esfuerzo de control ante perturbación de rampa, escalón y cambio de referencia. En la figura 7, se puede observar como el esfuerzo de control apenas llega a un 5 % para el escalón y a un 20 % para la rampa. Con respecto a la señal de error (en la figura 8), se puede observar que para el escalón se tiene una variación del 2 % y para la rampa de un 6 % y reacciona rápidamente. Ahora, se realiza con la función de fragility rings un diagrama de Nyquist para verificar la sensibilidad en la figura 9: Este resultado fue muy satisfactorio, porque muestra que el controlador es robusto, está dentro de los dos anillos de fragilidad y se encuentra lejos del anillo interior. Esto se debe a que durante la sintonización fue necesario bajar la velocidad de la respuesta para darle estabilidad. Y como resultado dio Desempeño Cambios en: Mp referencia 2.5 % escalón 3.5 % rampa 6.2 % Cuadro III ta2 % 5.19 s 5.88 s 8.11 s TABLA RESUMEN PARA PAR ÁMETROS DE DESEMPE ÑO PARA DISE ÑO 1. En la tabla III-B se puede observar como los tiempos de asentamiento son bastante pequeños y además el sobrepaso es bastante pequeño, para la rampa aparece un 6.2 % que es el más alto. Servo Control Control Regulatorio Mp % ta2 % [s] escalón 2.5 5.19 escalón rampa 3 6.2 5.88 8.11 Otro aspecto importante de destacar, es que se probó que el controlador funciona tanto para la planta real como para el modelo obtenido de manera muy similar. respectivamente, ante los cambios mencionados anteriormente. Diseño II Para este diseño se utilizó un controlador PID estándar de 2 GdL. Se utilizó una metodologı́a heurı́stica para hallar los parámetros adecuados del controlador y obtener las caracterı́sticas deseadas para el lazo cerrado. La metodologı́a consistió el fijar algunos de los parámetros del controlador y variar los demás hasta lograr la respuesta deseada. El primer parámetro fijado fue Td , el cual se utilizó para cancelar el polo del modelo MISOMT, luego se colocó Ti alejado diez veces de Td , se fijó gamma en cero para que la parte derivativa solo se aplique a la señal realimentada. Los parámetros libre, Kp y β se emplearon para ajustar la respuesta variado poco a poco sus valores hasta dar con una respuesta satisfactoria. III-C1. Parámetros del controlador: Como resultado del diseño se obtuvieron los parámetros de la tabla IV Kp Ti Td 0.005 β 17.24 [s] γ 1.69 [s] N Cuadro IV Respecto a la señal realimentada, se nota un comportamiento suave y con apenas oscilaciones en la respuesta, ante perturbaciones de tipo rampa o escalón, mientras que la respuesta en servo control ante escalones, no posee oscilación alguna. 65 60 55 y% III-C. 50 45 0.81 0 10 r(t):escalón d(t):escalón d(t):rampa 40 35 30 35 40 45 50 55 60 65 70 tiempo [s] PAR ÁMETROS DEL CONTROLADOR DEL DISE ÑO II Figura 11. Respuesta de la señal realimentada a cambios en las entradas. III-C2. Robustez y desempeño: En cuanto al las caracterı́sticas de desempeño como lo muestra la tabla III-C2 se obtiene valores de sobrepaso máximo y tiempo de asentamiento muy buenos, que cumplen con las especificaciones de diseño. Mp % 0 2.8 2.6 r(t)= u(t) d(t) = u(t) d(t) = rampa ta2 s 4.64 6 3.28 Por otro lado, la señal de control es suave ante cambios en la referencia o ante una entrada rampa en la perturbación, pero ante entrada escalón en la perturbación se obtiene un pico, lo cual no es deseable en esta señal, ya que puede causar un daño en el actuador. Sin embargo en la vida real un cambio escalón en la altura del UAV no es posible y las bolsas de aire no se deben consideran como escalones, sino como rampas de elevada pendiente. Por otro lado, la robustez se garantiza como se observa en la figura 10, por lo que la inexactitud del modelo de la planta se compensa, asegurando la estabilidad en la planta real. 10 r(t):escalón d(t):escalón d(t):rampa 8 1 Fragilidad para planta sintonizada con LGR 6 L(j ) u% M S=1.2 0.5 4 M S=2.0 2 -1 0 L(j ) L(j ) 0 -0.5 -2 35 40 45 50 55 60 tiempo [s] -1 -1.5 -2 -1.5 -1 -0.5 0 0.5 Figura 12. Respuesta de la señal de control a cambios en las entradas. L(j ) Figura 10. Diagrama polar del lazo de control del diseño II. III-C3. Simulaciones: Se probó el lazo de control ante cambios en el 10 % de la señal de referencia, para examinar servo control. En cuanto a la perturbación, esta se varió 10 % para simular el efecto de una bolsa de aire y también se aplicó una rampa para simular el efecto del viento. En las figura 11, 12 y 13, se pueden observar los cambios en la señal realimentada, de control y de error Finalmente como se observa en la figura 13, la señal de error tanto en servo control como en control regulatorio tiende a cero, cumpliéndose por lo tanto todos los criterios de diseños impuestos para asegurar una adecuada labor de control. este modelo por ser mucho más sencillo que el de la planta, ha permitido realizar todos los cálculos necesarios de una forma más simple que si se hubiera utilizado la planta real. 2.5 r(t):escalón d(t):escalón d(t):rampa 2 1.5 VI. e [m] 1 Se ha logrado identifica y modelar exitosamente la planta con un modelo de segundo orden, con un polo en el orı́gen y retardo para el control de altura de un UAV con un ı́ndice de error muy bajo. 0.5 0 -0.5 -1 30 40 50 60 70 80 90 100 tiempo [s] Figura 13. Respuesta de la señal de error a cambios en las entradas. IV. V. M ODELO CONTRA PLANTA Para poder comprobar que el modelo se aproxima lo suficiente a la planta real, se han calculado los ı́ndice de error entre las señales, los cuales se muestran en la figura 14 y en la tabla V: 75 planta modelo 70 65 y% 60 55 50 45 40 40 Se logró desarrollar dos controladores distintos para control regulatorio que son capaces de reaccionar rápidamente ante las perturbaciones y además no son frágiles. Para lazo cerrado, se tiene un tiempo de asentamiento y un sobrepaso muy pequeños, es decir, poseen un buen desempeño. D ISE ÑO Ó PTIMO De los controladores encontrados, el diseño II ha sido el que mejor se adapta a la necesidad de este proyecto. La razón principal por la que se ha elegido es porque es capaz de reaccionar más rápido ante perturbaciones, su señal de control es más suave. 35 30 C ONCLUSIONES 50 60 70 80 90 tiempo [s] Figura 14. Respuesta del modelo y la planta ante cambios en referencia y perturbación. IAE 2.414 ITAE 73.23 ISE 0.3814 Cuadro V I NDICES DE ERROR ENTRE LAS SE ÑALES REALIMENTADAS DE LA PLANTA Y EL MODELO . Estos ı́ndices de error son sumamente pequeños, esto quiere decir que este modelo se asemeja mucho a la realidad, por esta razón, el controlador ha funcionado correctamente con la planta real y la del modelo de forma muy similar, además Se realizaron distintas simulaciones para poder comprobar todos los datos anteriores con la herramienta Matlab y Simulink y se calcularon los ı́ndices de error para los casos en los que era pertinente. R EFERENCIAS [1] Mohammad Fiuzy, Javad Haddadnia, and Seyed Kamaleddin Mousavi Mashhadi. Designing an optimal pid controller for control the plans height, based on control of autopilot by using evolutionary algorithms. Journal of Mathematics and Computer Science, 06:260–271, 05 2013. [2] Mathworks. Pid controller tuning in simulink. https://la.mathworks.com/ help/slcontrol/gs/automated-tuning-of-simulink-pid-controller-block. html.