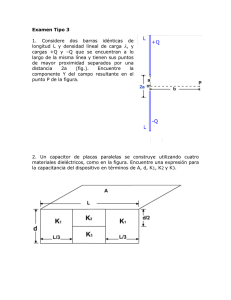
FACULTAD REGIONAL ROSARIO UDB BASICAS- Física Física II GUÍA DE PROBLEMAS 2: Electrostática 2da parte TEMAS: Potencial eléctrico Capacitancia Recopilación, revisión y edición: Ing. J. Santa Cruz, Ing. I. Arraña Coordinación: Ing. J. Farina Año 2018 1 Potencial eléctrico. 1) Dos cargas puntuales q1 = 40·10-9 C y q2 = - 30·10-9 C se encuentran ubicadas como indica la Figura 1. a) Determine el potencial en el punto A. b) Determine el potencial en el punto B. c) Determine el trabajo necesario para transportar una carga de 25·10-9 C desde el punto B hasta el A. Figura 1 Rta: a) VA=1800 V; b)VB= 0 V; c) WBA=4,5x10-5J 2) A cierta distancia de una carga puntual, el potencial y la magnitud del campo eléctrico debido a esa carga son 4,98 V y 12 V/m, respectivamente. (Considerar el potencial igual a 0 en el infinito) a) ¿Cuál es la distancia a la carga puntual? b) ¿Cuál es la magnitud de la carga? c) ¿EI campo eléctrico está dirigido hacia la carga puntual o se aleja de esta? Rta: a) 0,415 m; b) Q=2,30x10-10C; c) se aleja de la carga puntual. 3) Determine el trabajo que realiza el campo eléctrico para traer una carga positiva de 1·10-9 C desde el infinito a cada uno de los puntos A; B y C de la Figura 2. q1= 12x10-9C y q2= -12x10-9C. Analice el signo del trabajo. Rta.: WA= 9x10-7 J; WB= -1,93 x10-6 J; WC= 0 J Figura 2 4) Se colocan tres cargas puntuales iguales de 1,20 μC en las esquinas de un triángulo equilátero cuyos lados miden 0,5 m de longitud. ¿Cuál es la energía potencial del sistema? (Considere la energía potencial de las tres cargas igual a cero cuando se encuentren separadas por una distancia infinita). Rta.: 0,078 J 2 5) Una partícula con carga de +4,20 nC está en un campo eléctrico uniforme E dirigido hacia la izquierda. Se libera desde el reposo y se mueve a la izquierda. Después de que se ha desplazado 6 cm, su energía cinética es de +1,50 x 10-6 J. a) ¿Que trabajo realizó la fuerza eléctrica? b) ¿Cuál es el potencial del punto de inicio con respecto al punto final? c) ¿Cuál es la magnitud de E? Rta.: a) 1,50x10-6J; b)357 V; c)5952 N/C 6) Los dos electrodos planos, paralelos y horizontales de una válvula de vacío distan 2 cm y están conectados a 120 V. a) Determine la intensidad del campo eléctrico en el espacio comprendido entre las dos placas. b) Determine la fuerza eléctrica que actúa sobre un electrón ubicado entre los electrodos. Compare esta fuerza con la fuerza gravitatoria que actúa sobre el electrón. c) Determine la energía adquirida por un electrón que sale del cátodo y se dirige al ánodo a 2 cm de aquél. Rta.: a) E= 6000 V/m; b) Felec= 9,6x10-16 N y Fgrav=8,9x10-30N; c) ΔK=1,92x10-17 J 7) Dos esferas metálicas conductoras A y B, de 10 cm de radio cada una, están colocados de modo que sus centros distan 1 m. Si se da a la esfera A una carga de +30 nC y a la B de -60 nC. Calcular el potencial de cada una. Rta.:VA=2160 V y VB= -5130 V 8) El campo eléctrico en la superficie de una esfera de cobre con carga, sólida y con radio de 0,2 m es de 3800 N/C, dirigido hacia el centro de la esfera. ¿Cuál es el potencial en el centro de la esfera si se considera un potencial igual a cero a una distancia infinitamente grande con respecto a la esfera? Rta.:V= -760,5 V 9) Una esfera metálica con radio ra = 1,20 cm esta sostenida por un soporte aislante en el centro de una coraza esférica, hueca, metálica y con radio rb = 9,60 cm. En la esfera interior se coloca una carga +Q y en la exterior otra -Q. Se elige que la magnitud de Q sea tal que haga que la diferencia de potencial entre las esferas sea de 500 V, con la esfera interior a un potencial más elevado, a) Calcular la carga Q. 3 b) Elabore un diagrama de las superficies equipotenciales que correspondan a 500, 400, 300, 200, 100 y 0 V. c) En el diagrama indique las líneas de campo eléctrico. Rta.: a) 7,62x10-10 C; b) 400 V a un r= 4,45 cm, 300 V a un r= 2,53 cm, 200 V a un r= 4 cm y 0 V a un r= 9,6 cm 10) Calcular el campo eléctrico y el potencial de una distribución superficial de carga esférica de radio R (cáscara o esfera maciza conductora) de carga + Q. Dibujar la gráfica de E. Capacitancia 11) Dos placas de un capacitor plano están separadas 1 mm y tienen 1m2 de área. Las placas se encuentran en el vacío. Se aplica al capacitor una diferencia de potencial de 12000 V. Calcular: a) La capacidad. b) La carga de cada placa. c) La intensidad del campo eléctrico. Rta: a) C=8,85x10-9 F; b) Q= 106x10-6 C; c) 1,2x107 V/m 12) Un capacitor de 6 μF se conecta en serie con otro de 4 μF y entre ellos se aplica a diferencia de potencial de 200 V. a) ¿Cuál es la carga sobre cada capacitor? b) ¿Cuál es la diferencia de potencial entre cada capacitor? Rta.: a) 4,8x10-4 C; b) V1= 80V y V2=120 V 13) Un capacitor está formado por dos placas paralelas, planas y circulares, de 10 cm2 cada una, la cuales están separadas por un dieléctrico que llena totalmente el espacio entre las placas. El grosor del dieléctrico es 1 mm y su constante dieléctrica es 2,5. Si las láminas del capacitor se conectan a una batería de 100 V: a) La intensidad del campo eléctrico en el interior del capacitor. b) La capacidad del capacitor c) La carga de cada lámina 4 c) La energía eléctrica almacenada en el capacitor. Rta: a) E=100x103 V/m; b) C=2,21x10-11 F; c) 2,21x10-9C; d) U=1,105x10-7 J. 14) Un capacitor plano tiene placas cuadradas de 10 cm de lado y una separación de 4 mm. Un dieléctrico de constante k=2 tiene dimensiones de 10cm x 10cm x 4mm. a) Calcular la capacidad con el dieléctrico entre las placas. b) ¿Cuál sería la capacidad si el dieléctrico tuviera solo 3 mm de espesor? c) Si la rigidez dieléctrica del aislante es 50 V / mm, cuál debe ser el área mínima para mantener C. d) Calcular densidad de carga libre e inducida Rta.: a) 44,2 pF; b) 35,4 pF 15) En la configuración de la Figura 3, la carga sobre el capacitor C3 (5 μF) es 120 μC a) Determina la capacidad equivalente entre x e y. b) Determina la diferencia de potencial entre x y z. Rta.: a) Ceq= 5 µF; b) 64 V Figura 3 16) Un capacitor de 20 μF está cargado a una diferencia de potencial de 1000 V. Las armaduras de dicho capacitor se conectan en paralelo a uno descargado de 5 μF. a) Determina la carga inicial del sistema. b) Determina la diferencia de potencial final entre las armaduras de cada capacitor. c) Determina la disminución de energía cuando se conectan los capacitores. Rta.: a) Q=20x10-3 C; b)V=800 V; c)ΔU= 2J 17) Un capacitor de 1 μF y otro de 2 μF se conectan en serie a una red de suministro de 1200V. a) Calcular la carga de cada capacitor y su voltaje. b) Los capacitores cargados se desconectan de la red y ellos entre sí, y se vuelven a conectar en paralelo, con las armaduras del mismo signo unidas. Calcular la carga y el voltaje de cada uno. 5 Rta.: a) Q1=Q2= 8x10-4 C, V1= 800 V y V2=400 V; b) V1=V2=533,3 V, Q1= 5,33x10-4 C y Q2= 10,66x10-4 C 18) Un capacitor de 1μF y otro de 2 μF se conectan en paralelo en una línea de 1200V. a) Calcular la carga de cada capacitor y su voltaje. b) Los capacitores cargados se desconectan de la red y ellos entre sí, y se vuelven a conectar en paralelo, con las armaduras de distinto signo juntas. Calcular la carga final de cada uno y su voltaje. Rta.: a) Q1= 1,2x10-3; Q2= 2,4x10-3 C, V1=V2=1200 V; b) V1=V2=400 V, Q1= 0,4x10-3 C y Q2= 0,8x10-3 C 6 Problemas adicionales 1) Un campo eléctrico uniforme tiene una magnitud E y está dirigido en la dirección negativa de x. La diferencia de potencial entre el punto a (en x = 0,60 m) y el punto b (en x = 0,90 m) es 240 V: a) ¿Cuál punto, a o b, tiene el potencial más alto? b) Calcule el valor de E c) Una carga puntual negativa q = -0,2 μC se desplaza de b a a. Calcule el trabajo realizado por el campo eléctrico sobre la carga puntual. Rta.: a) Vb>Va; b)-800 V/m; c) Wba=-4,8x10-5 J 2) Una esfera pequeña con masa de 1,50 g cuelga de una cuerda entre dos placas verticales paralelas separadas por una distancia de 5 cm. Las placas son aislantes y tienen densidades de carga superficial uniformes de +σ y -σ. La carga sobre la esfera es q= -8,90 x 10-6 C. ¿Cuál diferencia de potencial entre las placas ocasionará que la cuerda formara un ángulo de 30° con respecto a la vertical? Rta.: 47,7 V 3) Practicamos en la esfera hueca (B) de radio 10 cm un orificio lo bastante grande para que pueda pasar la esfera (A) de 1 cm de radio y supongamos que la esfera (A) se encuentra en el centro de la esfera (B), como se muestra en la Figura 4. qA y qB son las cargas iniciales de las esferas. Figura 4 a) Calcular la diferencia de potencial VAB· b) ¿Qué ocurre si las esferas se ponen en contacto? Rta.: a) VAB=k·90·qA ; b) Se transfiere la carga de la esfera A a la B hasta que VAB=0. 4) En la Figura 5 se representan tres esferas conductoras concéntricas A, B y C. La esfera interior es maciza, de 10 cm de radio y tiene una carga eléctrica total nula; la esfera B es hueca, sus radios interior y exterior son 15 y 20 cm respectivamente y tiene una carga eléctrica total de -16 nC; la esfera C es hueca, sus radios interior y exterior son 25 cm y 30 Figura 5 7 cm, respectivamente y tiene una carga eléctrica total nula. a) Representar las líneas de campo eléctrico b) Diga cuál de las 3 esferas se encuentra a un mayor potencial eléctrico. Justificar la respuesta. Rta.: La esfera A se encuentra a mayor potencial. 5) Analice la Figura 6. 1- Al cerrar el interruptor 1, manteniéndose abierto el interruptor 2, se carga el capacitor C1 hasta alcanzar la diferencia de potencial de la fuente. 2- Después de cargado C1, se abre el interruptor 1 y se cierra el interruptor 2. Hecho esto, se mide la diferencia de potencial entre las placas del capacitor C2 y se observa un valor de 8,0 V. 3- A continuación, manteniendo cerrado el interruptor 2, se introduce entre las placas del capacitor C2 un dieléctrico D, cuya constante dieléctrica es K = 2,0, el cual llena totalmente el espacio entre las placas. Figura 6 a) Determine la energía entregada por la fuente al capacitor C1. b) Determine la energía que tiene el sistema de los dos capacitores cargados (sin dieléctrico). c) Determine la carga eléctrica que hay en las placas del capacitor C1 después de introducirse el dieléctrico entre las placas del capacitor C2. Rta.: a) U=3,4x10-9 J; b)U=0,38x10-9 J; c) Q1=5,76x10-11 C 4.- Determinar el campo eléctrico y el potencial en un punto cualquiera del espacio de una distribución lineal rectilínea de carga, de longitud infinita y densidad constante λ C/m. Bibliografía Sears – Zemansky – Young- Freedman . Física Universitaria con física moderna. 13 edición , Editorial: ADDISON WESLEY, 2014 Resnick –Halliday-Krane. Física Vol II. 5ta edición, Editorial: CECSA,2002 8 Serway-Jewett. Física para ciencias e ingeniería con física moderna. Vol 2. 7ma edición. Editorial: Cengage Learning Editores. 2009 http://fisicautn.wixsite.com/moliveros/guias-de-ejercicios 9