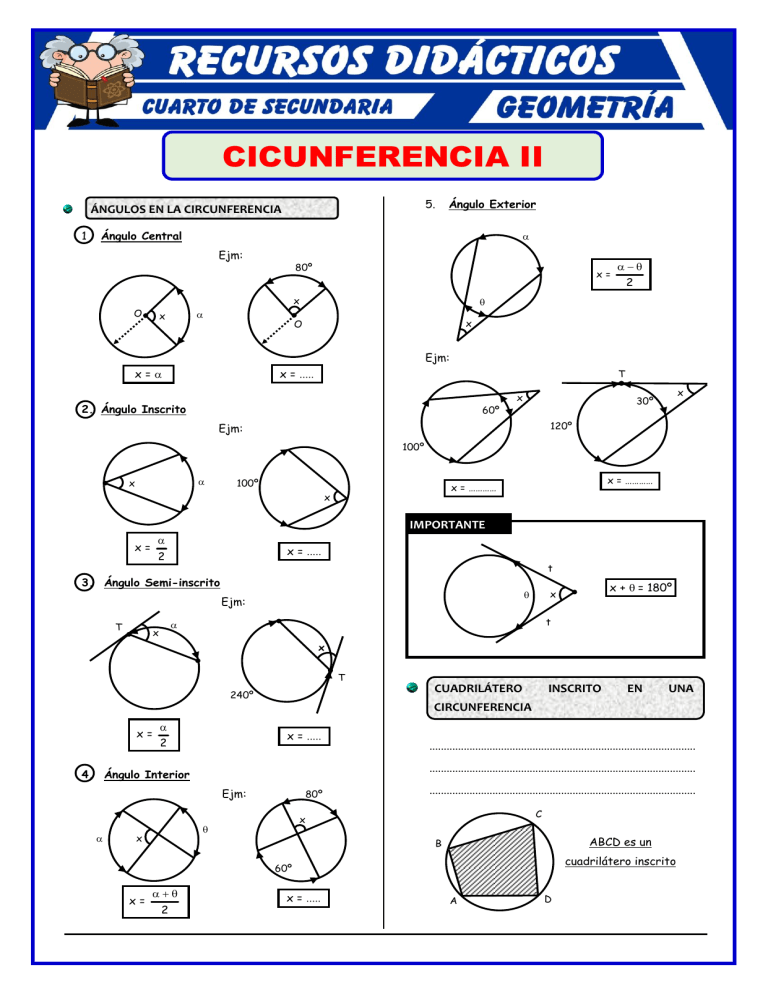
www.RecursosDidacticos.org CICUNFERENCIA II 5. ÁNGULOS EN LA CIRCUNFERENCIA 1 Ángulo Exterior Ángulo Central Ejm: 80º x= x O x 2 x O Ejm: x = x= T 2. Ángulo Inscrito 60º x x 30º 120º Ejm: 100º x 100º x = ………… x = ………… x IMPORTANTE x= x = 2 t 3. Ángulo Semi-inscrito T t x x + = 180º x Ejm: x T CUADRILÁTERO 240º INSCRITO EN UNA CIRCUNFERENCIA x= x = 2 ............................................................................................. 4. Ángulo Interior Ejm: 80º ............................................................................................. C x x ............................................................................................. ABCD es un B cuadrilátero inscrito 60º x= 2 x = A D www.RecursosDidacticos.org 1. .................................................................................. 2. .................................................................................. Calcular “x”, si “O” es centro a) 80º .................................................................................. b) 130º .................................................................................. c) 100º 50º d) 120º B = 180º 3. Calcular “” siendo A y B puntos de tangencia. A a) 40º D b) 30º c) 60º .................................................................................. d) 20º .................................................................................. e) 90º .................................................................................. B 4. C B Calcular “” 3 b) 22º c) 25º 5 d) 27º30’ D A a) 22º30’ 3. x e) 90º C A 2. o e) 18º30’ .................................................................................. 5. .................................................................................. Calcular “x”. Si mBC = 100º y A es punto de tangencia. A a) 65º .................................................................................. b) 50º B A x y x c) 75º C 25º d) 80º e) 25º x=y C NIVEL II D 6. Hallar la mAC = si mBD = 150º a) 80º EJERCICIOS DE APLICACIÓN D b) 60º 110º c) 75º d) 55º NIVEL I 1. a) 15º c) 35º 7. A P x d) 30º e) 60º B A e) 70º Calcular x, si mAPB = 300º b) 20º B B C Calcular “x”, si “O” es el centro. a) 35º b) 55º 30º c) 60º O 25º d) 50º e) 65º x www.RecursosDidacticos.org 8. En el gráfico. Calcular “x” 14. De la figura adjunta, mCD = 50º. Calcular “x” a) 36º E a) 25º b) 72º 3x c) 20º x b) 35º 2x c) 50º d) 30º d) 65º e) 53º e) 75º D C A 9. Calcular “x” 15. Se tiene un triángulo ABC, en el cual la circunferencia que pasa por los puntos medios de sus tres lados pasa también por el vértice B. 120º a) 60º b) 80º c) 70º Calcular la m B . x d) 30º a) 60º d) 90º 140º e) 40º 10. En la figura mostrada, hallar los valores de los arcos AF y PQ A a) 80º y 30º b) 100º y 50º b) 15º F c) 20º 80º a) 135º 2. 160º Calcular x, si mAB = mBC = 100º a) 50º d) 145º B x c) 80º x e) 130º A b) 40º B c) 155º d) 75º e) 160º O 12. La circunferencia está inscrita en el ∆PBC. Calcular “” B C 3. Calcular “x”, si AD es diámetro. E a) 56º a) 16º b) 51º 24º b) 32º c) 34º c) 35º d) 40º A P a) 80º A d) 46º 34º x B 4. C Hallar “x” si AB es diámetro y m∢PAC = 50º P a) 50º x b) 40º c) 75º D e) 68º C 13. Del gráfico. Calcular º + º si los polígonos sombreados son regulares. e) 58º O e) 25º A b) 150º d) 90º 4x d) 35º 11. Calcular “x”, si “O” es centro (A y B son puntos de tangencia) c) 74º Calcular “x”, si “O” es centro. a) 10º Q NIVEL III b) 60º c) 80º TAREA DOMICILIARIA 1. 35º d) 110º y 50º e) 100º y 40º b) 70º e) 12º P 75º c) 110º y 40º e) 24º B O d) 80º A B 50º e) 30º C www.RecursosDidacticos.org 5. Hallar “”, si P, Q y R son puntos de 11. Hallar (–), si : BC // AD tangencia; además la mAB = 80º B a) 100º c) 160º T d) 140º e) 200º 6. c) 80º Q 80º A R a) 10º 5 d) 30º e) 15º En la figura mostrada, calcular x donde A y B son puntos de tangencia. 36º 3x d) 54º e) 108º A D b) 80º C 80º 70º c) 135º D d) 150º F A b) 65º a) 100º d) 150º x c) 60º d) 30º e) 53º 10. Desde un punto exterior “P” se trazan dos rectas secantes a una misma circunferencia PAB y PCD. Hallar la m∢BPD, si mBD = 120º y BC b) 55º e) 40º B d) 40º 200º C M. Hallar la m∢AMB 80º a) 45º x A 15. Se tiene un cuadrante de circunferencia AOB, de centro O; sobre el arco AB se toma un punto E Del gráfico, calcular “x” D L c) 50º e) 60º e) 140º C a) 100º B b) 105º a) 65º d) 50º B a) 36º 14. Hallar “x”, si “B” es punto de tangencia B a) 120º c) 60º 13. Si: AB // CD , mBD = 72º y m∢DBC = 3(m∢ACB) Hallar la mAB e) 81º Calcular la m∢AFE AD b) 53º e) 106º d) 54º c) 12º 9. e) 75º c) 72º b) 36º 8. d) 90º b) 27º A a) 72º D A a) 30º d) 90º c) 12º 7. C 12. Calcular la medida del menor arco determinado por una cuerda en una circunferencia cuyo radio 5 es igual a de la longitud de dicha cuerda. 8 Calcular “” en la figura mostrada. b) 8º b) 60º P b) 80º B a) 45º c) 30º b) 120º e) 270º c) 135º