Práctica de las Leyes de Kepler: Campos Gravitatorios y Períodos Orbitales
Anuncio

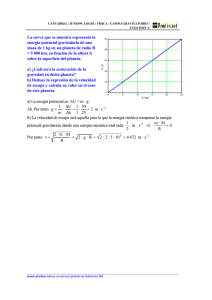
UNIVERSIDAD NACIONAL DE SAN AGUSTIN FACULTAD DE INGENIERIA GEOLOGICA, GEOFISICA Y MINAS ESCUELA PROFESIONAL DE INGENIERIA GEOLOGICA PROSPECCION GEOFISICA II TEMA: PRACTICA LAS LEYES DE KEPLER. INGENIERO: QUISPE MAMANI, RENZO DENNIS ALUMNO: PACOMPIA MAMANI, RICHARD AREQUIPA-PERU 2021 EJERCICIOS PROPUESTOS Ejercicio 1) Calcula el módulo del campo gravitatorio terrestre a una distancia de 500 km sobre la superficie de la Tierra. Datos: MT = 5,98 x 10²⁴kg, RT = 6370 km. 𝑔= 𝑔= 𝐺. 𝑀𝑇 𝐺. 𝑀𝑇 = 2 𝑀 (𝑅𝑇 + ℎ)2 6.67. 1011 ∗ 5.98. 1024 = 3.92 𝑁/𝐾𝑔 (6.37. 106 +505 )2 Ejercicio 2) Una partícula de masa m1 = 2 kg está situada en el origen de un sistema de referencia y otra partícula de masa m2 = 4 kg está colocada en el punto A (10,0). Calcula el campo gravitatorio en los puntos de coordenadas B (3,0) y C (5,3) y la fuerza que actúa sobre una partícula de 3 kg de masa situada en el punto C. 11 10 9 8 7 6 5 4 3 2 1 0 M=2Kg G2 G1 Ur1 A0 (0,0) 1 2 3 B (3,0) Ur2 A (10,0) 4 5 6 7 8 9 a) Campo gravitatorio en el punto B (3,0). 𝑚1 2 2 2 𝑢𝑟1 = −𝐺 32 𝑖 = −𝐺 9 𝑖 𝑟1 𝑚2 4 4 𝑔2 = −𝐺 2 𝑢𝑟2 = −𝐺 2 (−𝑖) = 𝐺 𝑖 3 9 𝑟2 𝑔1 = −𝐺 2 4 2 𝑔𝐵 = 𝑔1 + 𝑔2 = −𝐺 𝑖 + 𝐺 𝑖 = 𝐺 𝑖 = 1.48.10−11 𝑖 𝑁/𝐾𝑔 9 9 9 10 11 M=4Kg b) Campo gravitatorio en el punto C (5,3). El punto C está situado a la misma distancia de cada una de las partículas, aplicando el teorema de Pitágoras: d = 4 m. Los módulos de los campos creados por cada una de las partículas son: 𝑚1 2 2 𝑔1 = 𝐺 2 = −𝐺 2 𝑖 = −𝐺 34 𝑟1 √34 𝑚2 4 4 2 =𝐺 2 = 𝐺 34 𝑟2 √34 𝑔2 = 𝐺 Teniendo en cuenta la figura para determinar las relaciones trigonométricas de los respectivos ´ángulos y aplicando el principio de superposición, se tiene: 𝑔1𝑥 = 𝑔1 + 𝑠𝑒𝑛𝜑1 . (−𝑖) = −𝐺 𝑔2𝑥 = 𝑔2 + 𝑠𝑒𝑛𝜑2 . 𝑖 = 𝐺 𝑔𝑥 = 𝐺 2 3 6 𝑖 = −𝐺 𝑖 34 √34 34√34 4 5 20 𝑖=𝐺 𝑖 34 √34 34√34 14 34√34 𝑖 11 10 9 8 7 6 5 4 (5,3) 3 𝝋𝟏 2 √𝟑𝟒 1 0 𝝋𝟐 √𝟏𝟑 3 4 5 √𝟑𝟒 5 5 0 1 2 3 6 𝑔1𝑦 = 𝑔1 + 𝑐𝑜𝑠𝜑1 . (−𝑗) = −𝐺 𝑔2𝑦 = 𝑔2 + 𝑐𝑜𝑠𝜑2 . −𝑗) = 𝐺 𝑔𝑦 = 𝐺 7 8 9 2 √13 26 𝑖 = −𝐺 𝑖 16 √34 544 4 √13 52 𝑖=𝐺 𝑖 34 √34 544 26 𝑗 544 10 11 𝑔𝑐 = 𝑔𝑥 + 𝑔𝑦 = 𝐺 14 34√34 𝑔𝑐 = 𝑔𝑥 + 𝑔𝑦 = (4,71.10−12 − 3.19.10−12 )𝑁/𝐾𝑔 𝑔𝑐 = √𝑔𝑥2 + 𝑔𝑦2 = √(4,71.10−12 )2 + (3.19.10−12 )2 =5.68.10−12 c) La fuerza que actúa sobre la partícula colocada en el punto C es: 𝐹 = 𝑚. 𝑔𝑐 = 3(4,71.10−12 𝑖 − 3.19.10−12 𝑗) = (14.13.10−12 𝑖 − 9.57.10−12 𝑗)𝑁/𝐾𝑔 𝐹 = 𝑚. 𝑔𝑐 = 3(5.68 ∗ 10−12 ) = 17.04−12 𝑁 Ejercicio 3) Dos planetas de masas iguales orbitan alrededor de una estrella de masa mucho mayor. El planeta 1 describe una órbita circular de radio r1 = 10⁸ km con un periodo de rotación T1 = 2 años, mientras que el planeta 2 describe una órbita elíptica cuya distancia más próxima es r1 = 10⁸ km y la más alejada es r2 = 1,8 · 10⁸ km tal y como muestra la figura. ¿Cuál es el periodo de rotación del planeta 2? Aplicar la Ley de Kepler 𝑇12 𝑇22 = 𝑟13 𝑟23 1. Calcular la distancia media del planeta 2 a la estrella 𝑟= 𝑟= 𝑟1 + 𝑟2 2 108 + 1.8 ∗ 108 2 𝑟 = 1.4 ∗ 108 2. calcular el periodo de rotación del planeta 2: 22 𝑇22 = (108 )3 (1.4 ∗ 108 )3 22 (1.4 ∗ 108 )3 = 𝑇22 (108 )3 𝑇2 = √ 22 (1.4 ∗ 108 )3 (108 )3 𝑇2 = 3.31 𝑎ñ𝑜𝑠