8-Estadística, combinatoria y probabilidad

MATEMÁTICAS
NOTA
Tema: Estadística, combinatoria, probabilidad
Profesor:
Curso y grupo: 4º ESO
Fecha: 3-6-2014
Nombre:
ESTADÍSTICA
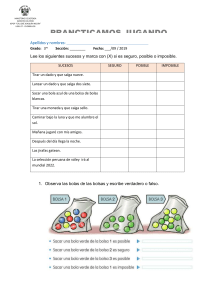
1. (1,5 puntos) Calcula las medidas de centralización de los siguientes datos y represéntalos en un diagrama de sectores:
ORDENADORES
0
1
2
3
HOGARES
18
36
27
9
2. (1,5 puntos) Calcula el coeficiente de variación de la siguiente variable estadística y representa los datos en un histograma:
NOTAS
[1, 3)
[3, 5)
[5, 7)
[7, 9)
ALUMNOS
12
8
14
10
3. (0,5 puntos) En una encuesta sobre el número de horas que se dedican al estudio diariamente, la media ha sido de 2 horas y
la desviación típica de 0,5 horas. En otra encuesta semejante, pero en otro instituto, la media ha sido de 3 horas y la
desviación típica 0,6 horas. ¿En qué instituto es mayor la dispersión de las horas de estudio? Justifica tu respuesta.
COMBINATORIA
4. (1,5 puntos) Con las letras de la palabra MATEMÁTICAS:
a.
b.
c.
¿Cuántas palabras se pueden formar de 4 letras distintas?
¿Y de siete letras distintas?
¿Y de cinco letras admitiendo repeticiones?
5. (1 punto) En una clase de 30 alumnos se quiere elegir delegado y subdelegado. ¿De cuántas maneras distintas se puede
hacer?
6. (1 punto) Calcula el término vigésimo cuarto de la potencia (3𝑥 2 − 𝑥)26 y simplifica el resultado.
PROBABILIDAD
7. (1 punto) En una urna hay diez bolas numeradas del 1 al 10. Se consideran los siguientes sucesos:
A = {sacar un número primo} y B = {sacar un número par}. Dados los siguientes sucesos, di qué sucesos elementales los
componen y calcula sus probabilidades:
a)
A∩B
b) A  B
c) A
d) A  B
8. (1 punto) En un bombo hay 49 bolas numeradas del 1 al 49. Se sacan seis bolas. ¿Qué probabilidad hay de acertar los seis
números?
9. (1 punto) En una urna hay 4 bolas rojas y 6 negras. Se sacan tres bolas de la urna. Calcula las probabilidades de los
siguientes sucesos:
a) Sacar tres bolas rojas sin reemplazamiento.
b) Sacar solo dos bolas rojas con remplazamiento.