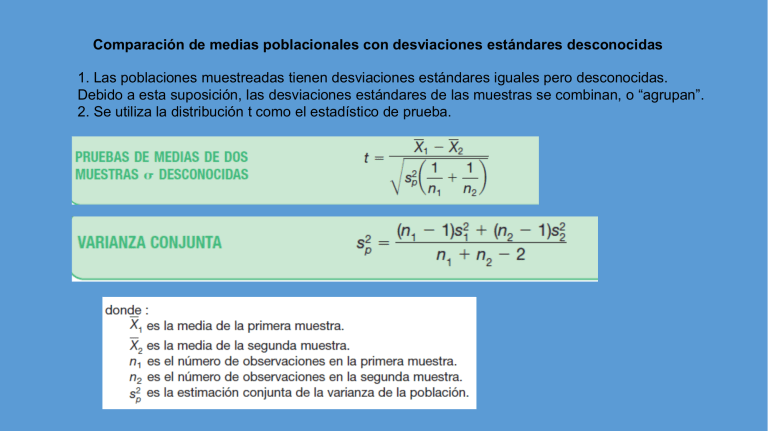
Comparación de medias poblacionales con desviaciones estándares desconocidas 1. Las poblaciones muestreadas tienen desviaciones estándares iguales pero desconocidas. Debido a esta suposición, las desviaciones estándares de las muestras se combinan, o “agrupan”. 2. Se utiliza la distribución t como el estadístico de prueba. El número de grados de libertad de la prueba es el número total de elementos muestreados menos el número total de muestras. Como hay dos muestras, hay n1 + n2 – 2 grados de libertad. En resumen, la prueba respeta tres requisitos o suposiciones. 1. Las poblaciones muestreadas siguen la distribución normal. 2. Las poblaciones muestreadas son independientes. 3. Las desviaciones estándares de las dos poblaciones son iguales. Se presenta en el cuadro siguiente el tiempo en minutos que se tardan en ensamblar un procesador a la placa principal en dos plantas distintas. ¿Existe alguna diferencia en el tiempo medio de montaje de los procesadores a la placa principal?. Para evaluar los dos métodos se realizo un estudio de tiempos y movimientos y se tomo una muestra de 5 empleados en la planta A y seis en la planta B y se midió el tiempo de montaje. Utilice un nivel de significancia de 0.10. A B 2 3 4 7 9 5 3 8 2 4 3 Ho: µ𝟏 = µ𝟐 gl= n1 + n2 – 2 = 5+6-2 = 9 H1: µ𝟏 ≠ µ𝟐 y α = 0.10 y es de dos colas la tabla da que t = ±1.833 A B 2 3 4 7 9 5 3 8 2 4 3 Media 𝑥1 =4 Media 𝑥2 =5 Desv esta=2.9155 Desv esta=2.0976 𝑠𝑃2 𝑛 − 1 𝑠12 + 𝑛 − 1 𝑠22 5 − 1 2.9155 2 + 6 − 1 2.0976 = = 𝑛1 + 𝑛2 − 2 5+6−2 𝑡= 𝑥1 −𝑥2 2 1+1 𝑠𝑃 𝑛1 𝑛2 = 4−5 6.222 1 1 + 5 6 2 = 6.222 = −0.662 La decisión es no rechazar la hipótesis nula, porque 0.662 se encuentra en la región entre 1.833 y 1.833. Se concluye que no existe diferencia entre los tiempos medios necesarios para ensamblar los procesadores El gerente de producción de Kaminar, fabricante de sillas de ruedas, desea comparar el número de sillas de ruedas defectuosas producidas en el turno matutino con el del turno vespertino. Una muestra de la producción de 6 turnos matutinos y 8 vespertinos reveló el número de defectos Siguiente: Matutino Vespertino 5 8 8 10 7 6 7 11 9 7 9 12 14 9 Con un nivel de significancia de 0.05, ¿hay alguna diferencia entre el número medio de defectos por turno? a) Formule las hipótesis nula y alternativa. b) ¿Cuál es la regla de decisión? c) ¿Cuál es el valor del estadístico de prueba? d) ¿Cuál es su decisión respecto de la hipótesis nula? A ) Ho: µ𝒎 = µ𝒗 H 1 : µ𝒎 ≠ µ𝒗 b) gl= n1 + n2 – 2 = 6+8-2 = 12 c) Media = 7 Desv esta=1.4142 𝑠𝑃2 y α = 0.05 y es de dos colas la tabla da que t = ±2.179 Media = 10 Desv esta=2.2678 𝑛 − 1 𝑠12 + 𝑛 − 1 𝑠22 6 − 1 1.4142 2 + 8 − 1 2.2678 = = 𝑛1 + 𝑛2 − 2 6+8−2 𝑡= 𝑥1 −𝑥2 2 1+1 𝑠𝑃 𝑛1 𝑛2 = 7−10 1 1 3.833 6+8 = −2.837 2 = 3.833 d) Se rechaza H0 porque 2.837 es menor que el valor crítico. Una empresa considera comprar baterías de respaldo para sus servidores y evalúa dos marcas, por lo que resume la información de las baterías Marca A: n1 = 10 Media 𝑥1 =32 horas S1= 5 horas Marca B: n2 = 12 Media 𝑥2 = 26 horas S2= 8 horas Con la información anterior, cree usted que es mejor la marca A que la B a un nivel de significación del 5 % Ho: µ𝑨 = µ𝑩 H1: µ𝑨 > µ𝑩 gl= n1 + n2 – 2 = 10+12-2 = 20 𝑠𝑃2 𝑡= y α = 0.05 y es de una cola la tabla da que t = 1.72 𝑛 − 1 𝑠12 + 𝑛 − 1 𝑠22 10 − 1 5 2 + 12 − 1 8 = = 𝑛1 + 𝑛2 − 2 10 + 12 − 2 𝑥1 −𝑥2 2 1+1 𝑠𝑃 𝑛1 𝑛2 = 32−26 46.45 1 1 + 10 12 = 2.056 1.72 2.056 2 = 46.45 Ho se rechaza y se acepta H1 Tienen mayor rendimiento las baterías de la marca B









