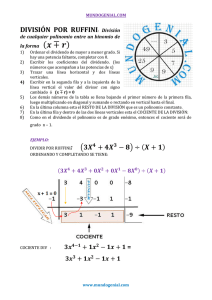
Guía Matemática 3. SESION 2 11-02-2023 III ciclo TEOREMA DEL RESIDUO Y TEOREMA DEL FACTOR MSc. Carlos Enrique Vasquez E. Propiedades de la división: La división o cociente es una operación matemática que consiste en repartir entre partes o grupos iguales y se representa mediante los símbolos "÷", ":" y "/", generalmente. La visión es el contrario de multiplicar. Si conoces un factor de la multiplicación entonces puedes encontrar un factor de la división. Por ejemplo, si 4 x 5 = 20, 20 / 5 = 4 y 20 / 4 = 5. Tipos de división Existen dos tipos de división dependiendo del resultado que obtengamos en el Resto: 1. División exacta: llamamos división exacta a la división cuyo resultado es cero. Dividendo = divisor x cociente 15 = 5 x 3 División entera o inexacta: llamamos división inexacta o entera a la división en la que el dividendo es igual al divisor por el cociente más el resto. Dividendo = divisor x cociente + resto 17 = 5 x 3 + 2 Propiedades de la división o Propiedades no conmutativas: en el caso de las divisiones, no se da la propiedad conmutativa. Al contrario de lo que sucede en la propiedad conmutativa de la multiplicación, si variamos el orden de los números de una división, se alterará el resultado. Por ejemplo: 10 ÷ 2 = 5, pero 2 ÷ 10 = 0, 2. o Propiedad no asociativa: si descomponemos uno o todos los números de una división, o los agrupamos de diferentes maneras, el cociente o el resultado pueden cambiar. Por ejemplo: 200 ÷ 10 ÷ 5 puede dar 4 o 100 según como se asocie. Si realizamos (200 ÷ 10) ÷ 5 = 20 ÷ 5 = 4, pero es diferente a 200 ÷ (10 ÷ 5) = 200 ÷ 2 = 100 o Propiedad distributiva: es válida la propiedad distributiva de la división cuando se descompone el dividendo. Por ejemplo: 400 ÷ 10 = 200 ÷ 10 + 200 ÷ 10 o Cero dividido entre cualquier número da cero: por ejemplo, "0: 7 = 7". o No podemos dividir por cero, ya que no existe ningún cociente que multiplicado por 0 sea igual al dividendo. División sintética o regla de Ruffini: La división sintética se puede decir que es una forma abreviada de dividir un polinomio por otro polinomio de primer grado. El método sintético implica encontrar ceros de los polinomios. Este tipo de división por un denominador lineal se conoce comúnmente como división por La regla de Ruffini Para que el método de división sintética sea posible, se deben cumplir los siguientes requisitos: • El divisor debe ser un factor lineal. Esto significa que el divisor debe ser una expresión de grado 1. • El coeficiente principal del divisor también debe ser 1. Si el coeficiente del divisor es distinto de 1, el proceso de división sintética se estropeará. Por lo tanto, se verá obligado a manipular el divisor para convertir el coeficiente principal a 1. Por ejemplo, 4x - 1 y 4x + 9 serían x - ¼ y x + 9/4 respectivamente. Teorema del Residuo Generalmente cuando un polinomio se divide entre un Binomio hay un residuo. Teorema del Factor Es una aplicación que vincula factores y ceros de un polinomio en específico. Es un caso especial que se utiliza para resolver el teorema del resto, por lo tanto, cuando se mencionan, deben ir juntos. El teorema establece que un polinomio f(x) tiene un factor (x – k) si y solo si f (k) = 0. O lo que también se podría entender que k es una raíz. Las siguientes afirmaciones se aplican a cualquier polinomio f(x): • El resto es cero cuando f(x) se divide exactamente por (x–c) • (x-c) es un factor de f(x) • c es la solución de f(x) • c es un cero de la función f(x), o f(c)=0 Ejemplos: 1.- Dividir x3 + 5x2 -2x - 24 entre x – 2 2.- Dividir x2 + 11x + 30 entre x + 5 3.- 2x3 + 5x2 + 9 entre x + 3 4.- Use la división sintética para dividir 3 x3 + 10x 2-6x −20 por x + 2. 5.- Divida -9x4 + 10x 3 + 7x 2-6 entre x − 1. 6.- f(x)=x 2 - 8 x + 6. Divida el polinomio entre el binomio x - 2. 7.- ¿Cuál es el residuo cuando el polinomio 6x3+4x2+7x+6 es dividido por x+2? 8.- Encuentra el residuo cuando 10x3+4x2−5x+10 es dividido por x+5. 9.- Encuentra el residuo cuando 2x3−5x2+4x+2 es dividido por (2x+1)