
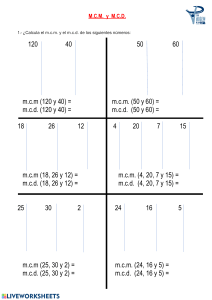
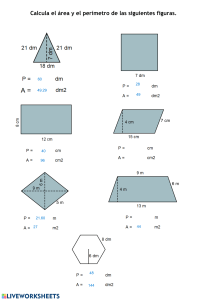
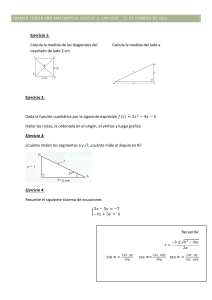
HOJA DE EJERCICIOS REPASO 4º ESO Matemáticas Académicas Tema 7: Trigonometría Curso 2017/18 1. Pasa los ángulos que están en grados a radianes, y viceversa: 2 3 a) 316º b) 10º c) 127º d) 3 rad e) rad f) rad 5 10 2. Calcula las siguientes razones trigonométricas, redondeando a dos decimales: a) sen 135º 34’ 12’’ b) cos rad c) tag 38º 3. Halla , en grados, minutos y segundos, sabiendo que: a) sen = 0,2573 b) cos = 0,7623 4. Resuelve el siguiente triángulo en cada uno de los casos: 5. Un árbol de 50 metros de alto proyecta una sombra de 60 metros de largo. Calcula el ángulo de elevación del sol en ese momento. 6. Un dirigible que está volando a 800 metros de altura, distingue un pueblo con un ángulo de 12º. ¿A qué distancia del pueblo se halla? 7. a) Escribe y demuestra las razones trigonométricas de 30º, 45º y 60º. b) Dibuja una circunferencia goniométrica y calcula las razones trigonométricas de 0º, 90º, 180º y 270º 8. Sin utilizar la calculadora: 2 a) Si sen = , calcula cos y tag . 5 1 b) Si cos = , calcula sen y tag . 3 3 c) Si tag = , calcula sen y cos . 4 9. Indica en que cuadrante estarán los siguientes ángulos. Dibújalos aproximadamente, así como sus razones trigonométricas seno y coseno. 7 a) 192º b) 25º c) 105º d) 312º e) rad f) rad 4 4 RESOLUCIÓN DE TRIÁNGULOS 10. De un triángulo rectángulo ABC conocemos la hipotenusa a=12 cm, y el cateto c=7cm. Halla sus ángulos agudos. 11. De un triángulo ABC conocemos c = 63 m, B̂ = 42º y  = 83º. Calcula el lado a. 12. De un triángulo ABC conocemos a = 4cm, B̂ = 30º y b = 5cm. Calcula el ángulo  . 13. Calcula el área del triángulo ABC: 14. En lo alto de un edificio en construcción hay una grúa de 4 m. Desde un punto del suelo se ve el punto más alto de la grúa bajo un ángulo de 50° con respecto a la horizontal, y el punto más alto del edificio bajo un ángulo de 40° con la horizontal. Calcula la altura del edificio. 15. Dos amigos están en una playa a 150 m de distancia y en el mismo plano vertical que una cometa que se encuentra volando entre ambos. En un momento dado, uno la ve con un ángulo de elevación de 50° y el otro con un ángulo de 38°. ¿Qué distancia hay de cada uno de ellos a la cometa? 16. Calcula el área de un triángulo del que se conocen los tres lados: 10, 8 y 7 metros. 17. En el centro de un lago sale verticalmente un chorro de agua, y queremos medir su altura. Para ello medimos el ángulo de elevación desde la orilla, obteniendo 43º, y alejándonos 100 metros volvemos a medir con el teodolito y obtenemos 35º. Calcula la altura del chorro de agua. SOLUCIONES 1. a) 5,51 rad b) 0,17 rad c) 2,21 rad 2. a) 0,7 c) 0,78 b) -1 3. a) = 14º54’35’’ d) 171º53’14’’ e) 72º f) 54º b) = 40º19’57’’ 4. a) A=90º ; C=48.3º ; b=3’33 m ; c=3’73 m b) A=90º ; C=35.4º ; a=3’68 m ; c=2’13 m c) A=90º ; B=41.8º ; C=48.2º ; c=4’47 m d) A=90º ; B=30.96º ; C=59.03º ; a=5.83 m 5. El ángulo es 39º48’20’’ 6. Está a 3.847 metros 7. Hecho en clase y en el libro. Es para practicar. 21 2 21 ; tag = 5 21 2 2 b) sen = ; tag = 2 2 3 3 4 c) sen = ; cos = 5 5 8. a) cos = 9. a) Tercero 10. b) Primero Cˆ 35º 41'7.2 '' ; Bˆ 54º18'53'' 11. a=76,34 m. 12. c) Segundo  =23º34’41’’ 13. 150,24 cm2 14. 9’5 metros 15. 92,41 m y 114,98 m 16. 27,81 m2 17. 281,07 m. d) Cuarto e) Primero f) Cuarto


![Evaluación%20Grado%20Decimo%20noveno%20y%20undecimo[1].](http://s2.studylib.es/store/data/000860011_1-723727629aa8ab5007657ff23e4e4a09-300x300.png)



