chulpolinomios
Anuncio

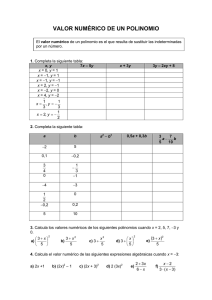
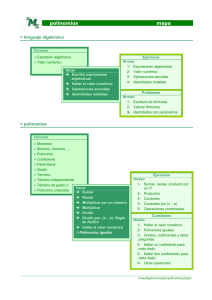
polinomios lenguaje algebraico Expresión algebraica: Combinación de números, letras, signos y operaciones. 2πR 2 3 5a b c Valor numérico: − b ± b 2 − 4ac 2a Es el que se obtiene al cambiar las letras por números y efectuar las operaciones. polinomios n n-1 2 p(x) = an x + an-1 x + ... + a2 x + a1 x + a0 Regla de Ruffini: Para dividir por (x – a) Grado: n El mayor exponente de x n an x Valor numérico: p(a) an Es el que se obtiene al cambiar x por un número Operaciones: Suma p(x) + q(x) Resta p(x) - q(x) Producto por un nº k . p(x) Producto p(x) . q(x) Cociente p(x) : q(x) n-1 + an-1x 2 + ... + a2x an-1 (x – a) a a2 + an * n-1 bn-2 n-2 Cociente: an x + bn-2 x grado n-1 + a1 x a1 + ... * + a0 b1 + ... + b1 x a0 + * b0 + * R + b0 Resto: R factorizar α n β p(x) = an x + ... + a1 x + a0 = an (x-a) (x-b) ... (ax2 +bx+c) Factores primarios: De 1º grado: (x – a) 2 De 2º grado: (ax +bx+c) Teorema del resto: p(a) = resto p(x) x–a Raíces: p(a) = 0 Valores de x que hacen cero el polinomio. Las raíces enteras son siempre divisores del término independiente, a0 consecuencia resto 0 ⇔ p(a) = 0 ⇔ a es raíz ⇔ (x–a) es factor Teorema fundamental del Álgebra: Un polinomio de grado n tiene n raíces pero pueden ser enteras, fraccionarias, reales o complejas y difíciles de calcular fracciones algebraicas p(x) q(x) Fracción algebraica: Fracción con polinomios en el numerador y el denominador. Operaciones: Como las fracciones de números. Valor numérico: El que se obtiene al cambiar las letras por números. nombre curso xms/algebra/chuletas /polinomios