ejersisgau31
Anuncio
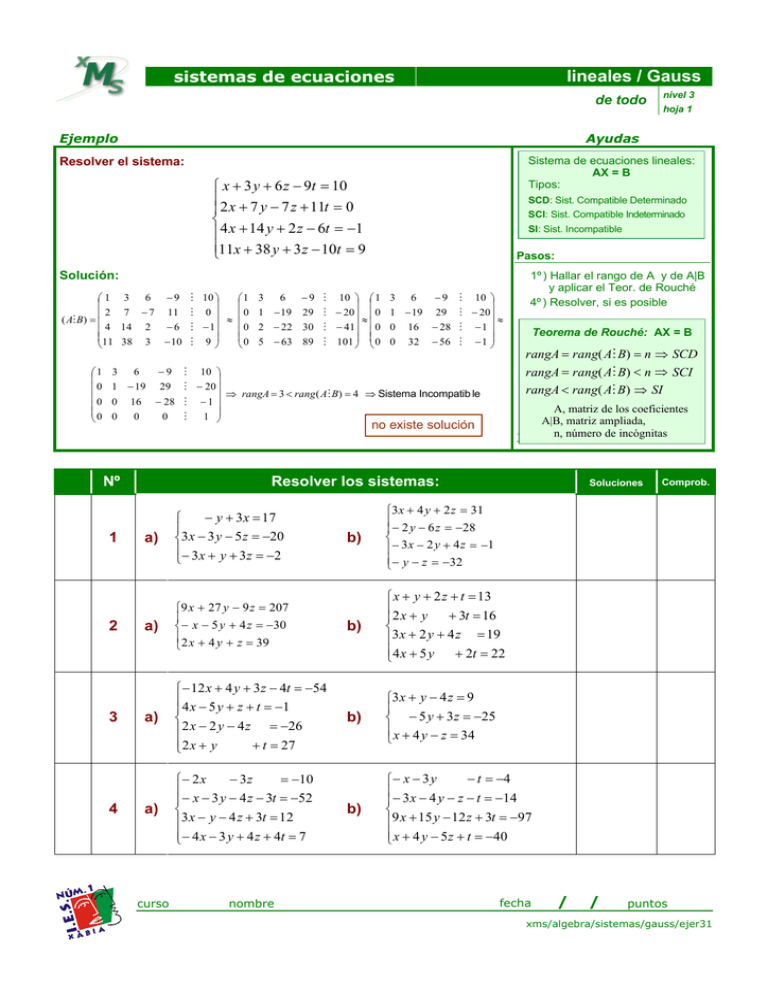
sistemas de ecuaciones lineales / Gauss de todo Ejemplo Sistema de ecuaciones lineales: AX = B Tipos: x + 3 y + 6 z − 9t = 10 2 x + 7 y − 7 z + 11t = 0 4 x + 14 y + 2 z − 6t = −1 11x + 38 y + 3 z − 10t = 9 SCD: Sist. Compatible Determinado SCI: Sist. Compatible Indeterminado SI: Sist. Incompatible Pasos: Solución: 1 0 0 0 3 7 6 −7 14 38 2 3 3 6 1 − 19 0 0 16 0 6 −9 − 9 M 10 1 3 − 11 M 0 0 1 19 29 ≈ 0 2 − 22 30 − 6 M −1 0 5 − 63 89 − 10 M 9 2 3 4 M 10 1 M − 20 0 ≈ M − 41 0 M 101 0 3 6 1 − 19 0 0 16 32 −9 29 M 10 M − 20 ≈ − 28 M − 1 − 56 M − 1 −9 29 M 10 M − 20 ⇒ rangA = 3 < rang ( AM B) = 4 ⇒ Sistema Incompatib le − 28 M − 1 0 M 1 1º ) Hallar el rango de A y de A|B y aplicar el Teor. de Rouché 4º ) Resolver, si es posible Teorema de Rouché: AX = B rangA = rang( AM B) = n ⇒ SCD rangA = rang( AM B) < n ⇒ SCI rangA < rang( AM B) ⇒ SI A, matriz de los coeficientes A|B, matriz ampliada, 3333 n, número de incógnitas no existe solución Nº 1 hoja 1 Ayudas Resolver el sistema: 1 2 ( AMB) = 4 11 nivel 3 Resolver los sistemas: a) − y + 3 x = 17 3 x − 3 y − 5 z = −20 − 3 x + y + 3 z = −2 a) 9 x + 27 y − 9 z = 207 − x − 5 y + 4 z = −30 2 x + 4 y + z = 39 a) − 12 x + 4 y + 3 z − 4t = −54 4 x − 5 y + z + t = −1 2 x − 2 y − 4 z = −26 2 x + y + t = 27 a) − 3z = −10 − 2 x − x − 3 y − 4 z − 3t = −52 3 x − y − 4 z + 3t = 12 − 4 x − 3 y + 4 z + 4t = 7 curso nombre Soluciones b) 3 x + 4 y + 2 z = 31 − 2 y − 6 z = −28 − 3 x − 2 y + 4 z = −1 − y − z = −32 b) x + y + 2 z + t = 13 2 x + y + 3t = 16 3 x + 2 y + 4 z = 19 4 x + 5 y + 2t = 22 b) 3 x + y − 4 z = 9 − 5 y + 3 z = −25 x + 4 y − z = 34 b) − t = −4 − x − 3 y − 3 x − 4 y − z − t = −14 9 x + 15 y − 12 z + 3t = −97 x + 4 y − 5 z + t = −40 fecha / / Comprob. puntos xms/algebra/sistemas/gauss/ejer31