Curso 05/06 (Segundo Parcial)
Anuncio

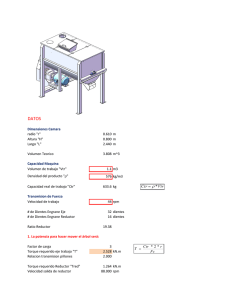
Asignatura: Vibraciones Mecánicas. Curso 2005/06 (2o Parcial) TEORÍCO-PRÁCTICAS (4 puntos cada pregunta) 1. En una instalación industrial se tiene una máquina compuesta por un motor eléctrico, reductor y compresor. Se observa que la máquina tiene un nivel anormalmente alto de vibraciones en reductor por un posible desgaste de los dientes de uno de los ejes. Se decide tomar una medida con un analizador de vibraciones en dirección radial sobre el rodamiento del eje de entrada para analizar el espectro. En función de los datos constructivos, razonar la frecuencia de muestreo y número de líneas se deben escoger en el analizador para poder estudiar este problema. Frecuencia muestreo (Hz) Numero de líneas 16 1 2.5 5 10 25 50 100 250 500 1000 2500 5000 10000 25000 50000 100000 250000 500000 32 64 Datos del motor: Potencia: 10kW Velocidad en medición: 1800 rpm 128 256 512 1024 2048 4096 8192 16384 32768 Datos del reductor: Eje de entrada con rueda 16 dientes Eje intermedio con 24 dientes (entrada) Eje intermedio con 30 dientes (salida) Eje de salida con rueda 45 dientes 2. Se tiene el sistema mecánico de la figura, compuesto por una varilla AD rígida de longitud L=1 m y masa m=30 kg. Está articulada en el L/3 L/3 L/3 F(t) extremo A de la varilla y en el extremo derecho se B C A acopla una masa puntual M igual a 50 kg. En los puntos m M B y C (AB=L/3 y AC=2L/3) se acopla un resorte de D c k rigidez k=2000 N/m y un amortiguador de coeficiente de amortiguamiento c=10 Ns/m, respectivamente. El sistema está inicialmente en reposo en su posición de equilibrio estático. Si se aplica una fuerza F(t) de la F(t) figura, con F0=500 N y a=10 s. Determínese el sistema equivalente para el estudio de las vibraciones F0 torsionales y respuesta θ(t) en cualquier instante. a t Nota: Se puede emplear cualquier método para su resolución y solo se deberá dejar planteada las diferentes ecuaciones para obtener la respuesta (no es necesaria la resolución completa). PROBLEMA nº1 (6 Puntos) Se tienen dos masas m iguales que solamente se puede desplazar verticalmente según se muestra en la figura. Cada una de las masas está acoplada al techo por un resorte de rigidez k y a la otra masa por un resorte de rigidez k. Determínese: k (a) Ecuaciones dinámicas para el estudio del sistema mecánico. x (t) 1 (b) Frecuencias propias de vibración y modos de mm k vibración. (c) Movimiento del sistema si se desplaza la masa 1 una distancia x0 de la posición de equilibrio en k ausencia de excitación exterior, es decir fuerza F(t). (d) Movimiento del sistema si sobre la masa 2 se F(t) mm x2(t) aplica una fuerza armónica F(t)=F0⋅sen(ωt) y el sistema está inicialmente en reposo. PROBLEMA Nº2 (6 Puntos) En un barco se observa un nivel alto de vibraciones con una pérdida de rendimiento. La máquina está compuesta por un volante de inercia, un motor, una caja de engranajes, un eje y por último la hélice de propulsión del barco. Para detectar la causa del problema se efectúa un análisis en frecuencia midiendo la vibración sobre el reductor en dirección vertical. En función de los datos constructivos, razonar justificadamente cuáles son los defectos que sufre la máquina. Características técnicas Datos del reductor: Datos del motor: Velocidad de giro del motor: entre 400 y 900 rpm Velocidad del motor durante la medida=900 rpm Número de palas de la hélice=3 Diámetro de los ejes=70 mm Volante de Inercia Engranajes Eje 1 Medida Helice Motor Eje 2 Eje de entrada (motor) con rueda 26 dientes Eje de salida (hélice) con rueda 15 dientes Rodamientos de la máquina (Tipo 1): Diámetro de bolas: 22.5 mm Número de bolas: 13 Diámetro pista interior: 80 mm Diámetro pista exterior: 110 mm Angulo de contacto: 0º 1.6 1.4 Amplitud (mm/s) 1.2 1.0 0.8 0.6 0.4 0.2 0.0 0 20 40 60 80 100 120 Frecuencia (Hz) 140 160 180 200