El Análisis Factorial de Correspondencias Múltiples es un

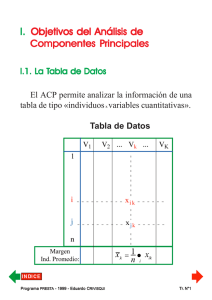
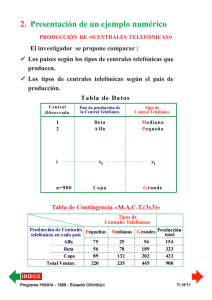
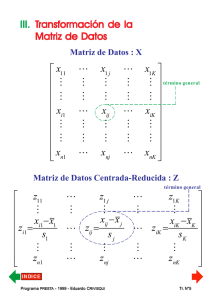
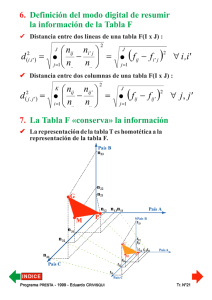
SEGUNDA PARTE
PRESENTACIÓN DEL MÉTODO
ANÁLISIS FACTORIAL
DE CORRESPONDENCIAS
MÚLTIPLES
DE
L. GENERALIZACIÓN DEL A.F.C. :
ANÁLISIS FACTORIAL DE
CORRESPONDENCIAS MÚLTIPLES
1. Introducción
➩ Las «encuestas» se organizan en torno a «unidades temáticas» que resultan del cuadro conceptual del estudio.
➩ Las «unidades temáticas» de una encuesta determinan la
estrategia de observación, pero también la estrategia de
análisis de datos.
➩ Por medio de «encuestas», se elaboran tablas que resumen
las p características observadas sobre n unidades de observación.
➩ La construcción del objeto de estudio se hace mediante el
tratamiento de la información contenida en esas tablas.
➩ El Análisis Factorial de Correspondencias Múltiples es un
instrumento adaptado al tratamiento estadístico de los datos
producidos por vía de «encuestas».
➩ Este método de análisis estadístico responde a una doble
exigencia : objetividad en el proceso de reducción y de
exploración de lo observado ; tratamiento de la información
con el nivel de síntesis adecuado al cuadro conceptual utilizado.
¿Por qué decimos que el AFCM responde a las exigencias
metodológicas de la investigación en ciencias sociales...?
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°99
Algunos errores (muy) comunes...
î
î
ΠPrimer error :
Se ignora el cuadro conceptual con el cual se organizó el
estudio. Se responde a la demanda del investigador
elaborando las p x q tablas de contingencia que cruzan p
características con otras q características observadas...

Segundo error :
Se seleccionan las «tablas interesantes» en función del
grado de significación estadística del test de independencia
hecho automáticamente sobre todas esas Tablas de Contingencia calculadas...
La información que interesa al investigador está dada por
algunas «tipologías» de las n unidades observadas.
î
Ž Tercer error :
Esas tipologías son construidas «subjetivamente»...
El A.F.C.M. de los datos de una encuesta permite la descripción y la exploración de lo observado para forjar descriptores
objetivos con el mismo nivel de síntesis con el que se pensó el
objeto de estudio.
El A.F.C.M. puede ser presentado como una simple
generalización del A.F.C. simples.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°100
2. Tablas estadísticas de resumen
de la observación
El investigador dispone :
F de un protocolo normalizado de encuesta.
F de una lista estándar de características observables
definidas con atributos mutuamente exclusivos.
Observando la j-ésima característica sobre el i-ésimo individuo, se puede afectar —sin ambigüedad alguna— la k-ésima
modalidad de la j-ésima característica al i-ésimo individuo.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°101
3. Tablas de Códigos Condensados
Tabla de Códigos Condensados TCC (n x p)
✘
Cada línea contiene todos los códigos correspondientes a
las modalidades atribuidas a un individuo, para cada una
de las características observadas.
✘
En la intersección de lai-ésima línea y de la j-ésima columna
figura el valor kij : código numérico que fue dado a la
modalidad «atribuida» al i-ésimo individuo para la j-ésima
característica observada.
✘
Tratándose de una tabla de códigos, la tabla TCC (n x p) no
posee propiedades numéricas.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°102
4. Tablas Lógicas
✘ A partir de la Tabla de Códigos Condensados se genera
una tabla numérica que resume la misma información.
Considerando la primera columna de la tabla TCC (n x p)...
En la Tabla TL(n x 3) asociada a la 1° columna de
la TCC(n x p) :
✘
x i1 = 1, si k i1 = 1, si k i1 = 2 o k i1 = 3
⇒
x i1 = 0
x i2 = 1, si k i1 = 2 , si k i1 = 1 o k i1 = 3
⇒
x i2 = 0
x i3 = 1, si k i1 = 3, si k i1 = 1 o k i1 = 2
⇒
x i3 = 0
La Tabla TL(n x 3) contienen las tres «variables indicadoras» de las modalidades de la 1° característica observada
(variables de presencia-ausencia).
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°103
5. Tabla Disyuntiva Completa
✘ Creando las Tablas Lógicas para cada
columna de la
TCC(n x p), podemos asociar a ella una TDC(n x K).
TABLA DISYUNTIVA COMPLETA
CORRESPONDIENTE A LA TABLA TCC(n x p)
-
K : total de modalidades de las p características observ.
Margen en columna de la tabla TDC = p, cte.
-
Margen inferior de la tabla TDC = distribución de frecuencias brutas de las p características observadas.
✘
La TDC(n x K) resume lo observado en los mismos
términos que la TCC(n x K) correspondiente.
✘
La TDC(n x K) presenta propiedades numéricas.
✘
La TDC(n x K) : tabla de correspondencias de tipo
particular.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°104
6. Tabla de Burt
TABLA DE BURT TB (K x K)
✘
La Tabla de Burt TB(K x K) es una tabla simétrica.
✘
La Tabla de Burt TB(K x K) es una tabla de correspondencias de tipo particular.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°105
La Tabla de Burt TB(K x K) presenta :
➧
En la intersección de la j-ésima línea y de la j-ésima
columna, el valor njj : número de individuos que presentaron la j-ésima modalidad de una característica dada,
➧
En la intersección de la j-ésima línea y de la k-ésima
columna, el valornjk= 0 si la j-ésima modalidad y lak-ésima
modalidad pertenecen a una misma característica observada,
➧
En la intersección de la q-ésima línea y de la k-ésima
columna, el valor nqk , es decir el número de individuos que
presentaron, simultáneamente, la q-ésima modalidad de
una característica dada y la k-ésima modalidad de otra
característica observada.
➧
En la diagonal, la distribución de frecuencias brutas de
todas las modalidades de todas las variables cualitativas
consideradas.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°106
M. OBJETIVOS DEL ANÁLISIS FACTORIAL
DE CORRESPONDENCIAS MÚLTIPLES
➊
Facilitar la construcción de tipologías de
individuos, mediante la comparación de todas las unidades de observación a través de
todas las modalidades de las características
observadas.
➋
Estudiar la relación existente entre las
características observadas.
➌
Resumir el conjunto decaracterísticas observadas en un pequeño número de
variables cuantitativas relacionadas con
el conjunto de variables cualitativas
estudiado.
➍
Estudiar la relación existente entre las
modalidades de las características
observadas.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°107
N. ANÁLISIS FACTORIAL DE CORRES_PONDENCIAS DE UNA TDC (n x K)
1. Distancia entre «individuos» (líneas) de
una TDC(n x K)
✔
j-ésima coordenada del i-ésimo individuo :
xij
xij
nj
xij
np
1
fij =
; fi. = ; f. j = ;
=
np
n
np 1 n j
nj
p
n np
np
✔
j-ésima coordenada del i'-ésimo individuo :
xi' j
xi' j
nj
xi' j
np
1
f i' j =
; fi'. = ; f . j = ;
=
np
n
np 1 n j
nj
p
n np
np
✔
Distancia del Chi2 entre los puntos-ind. i e i' :
2
d(2i ,i' )




K
xij
xi' j 

=∑
−
=
nj
nj 
j =1 
p
p

np
np 

2
d
2
( i ,i' )
K
2
np  xij xi' j 
n
1
=∑  −
= ∑ (xij − xi' j )

p 
p j =1 n j
j =1 n j
 p
K
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°108
Distancia del Chi2 entre los puntos-ind. i e i'
d
✔
2
( i ,i' )
K
2
1
n
= ∑ (xij − xi' j )
p j =1 n j
para cada término de esa sumatoria, la expresión (xij - xi'j)2
no puede valer más que 1 o 0.
✔ese factor vale 1 solamente si los dos individuos considerados
no presentan simultánemente la j-ésima modalidad,
✔ese factor vale 0 en el caso contrario (presencia simultánea o
ausencia simultánea de la j-ésima modalidad).
✔La distancia entre los individuos crece a medida que aumentan las diferencias de modalidades presentadas por ellos.
✔Cada modalidad interviene en el cálculo de la distancia entre
dos individuos con el factor n/nk ( inversa del peso de la
modalidad). La distancia entre los individuos será más
grande si presentan el mismo número de divergencias a
propósito de modalidades muy poco frecuentes (de bajo
peso).
➨La distancia del Chi2 entre individuos de una Tabla Lógica
respeta el criterio de comparación de individuos que hemos
adoptado.
Pr
ograma PREST
do CRIVISQ
A - 1999 - Eduar
UI
Programa
Eduardo
PRESTA
RIVISQUI
Tr. N°109