→ B = B = dl
Anuncio

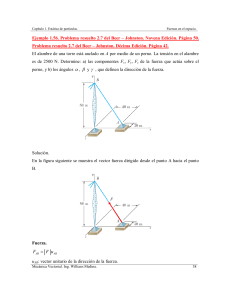
Campo magnético debido a una corriente rectilínea e indefinida ........ → B = I 4 ¶ → d l xr̂ corriente r 2 Cos α = Sen β I El sentido del vector inducción lo da en → cada punto el producto vectorial d l xr̂ (regla del B d l sacacorchos = Maxwell de la mano izqda.) o la regla de Maxwell de la mano dcha. En cualquier punto a distancia d de la corriente el módulo del vector inducción ha de ser el mismo por simetría: dl β r → para un d l mismo l, d, r , α y β. Vistas la dirección y sentido del vector vamos a calcular su módulo: ¶ I dlCos 4 corriente r 2 . Si tenemos en cuenta que Tgα=l/d dl=dTgα; d Derivando l respecto de α d(dl/dα)=d/Cos2αddl = d Cos 2 B= d Cos α= r d2 Cos 2 . Si tenemos en cuenta las dos líneas anteriores: d + 2 I I =+ 2 d Cos 2 .Cos I = 4d Cosd = 4d 2 d2 4 =− 2 −2 d r2 = B= ¶ ¶ Cos 2 B= I 2d α