Hoja de ejercicios 4 Econometría II Curso 2011/2012

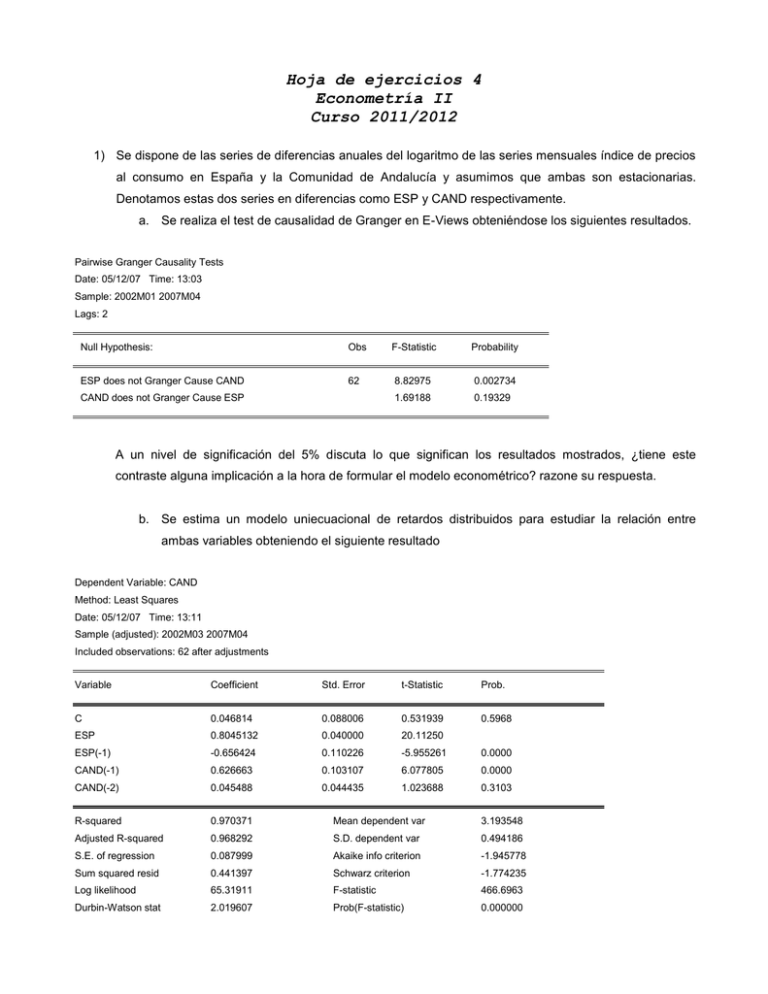
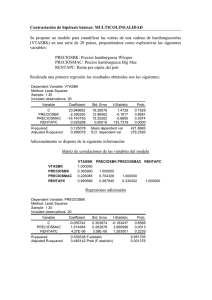
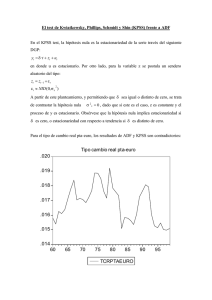
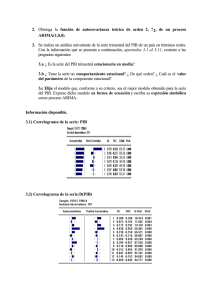
Hoja de ejercicios 4
Econometría II
Curso 2011/2012
1) Se dispone de las series de diferencias anuales del logaritmo de las series mensuales índice de precios
al consumo en España y la Comunidad de Andalucía y asumimos que ambas son estacionarias.
Denotamos estas dos series en diferencias como ESP y CAND respectivamente.
a. Se realiza el test de causalidad de Granger en E-Views obteniéndose los siguientes resultados.
Pairwise Granger Causality Tests
Date: 05/12/07 Time: 13:03
Sample: 2002M01 2007M04
Lags: 2
Null Hypothesis:
Obs
F-Statistic
Probability
ESP does not Granger Cause CAND
62
8.82975
0.002734
1.69188
0.19329
CAND does not Granger Cause ESP
A un nivel de significación del 5% discuta lo que significan los resultados mostrados, ¿tiene este
contraste alguna implicación a la hora de formular el modelo econométrico? razone su respuesta.
b. Se estima un modelo uniecuacional de retardos distribuidos para estudiar la relación entre
ambas variables obteniendo el siguiente resultado
Dependent Variable: CAND
Method: Least Squares
Date: 05/12/07 Time: 13:11
Sample (adjusted): 2002M03 2007M04
Included observations: 62 after adjustments
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
0.046814
0.088006
0.531939
0.5968
ESP
0.8045132
0.040000
20.11250
ESP(-1)
-0.656424
0.110226
-5.955261
0.0000
CAND(-1)
0.626663
0.103107
6.077805
0.0000
CAND(-2)
0.045488
0.044435
1.023688
0.3103
R-squared
0.970371
Mean dependent var
3.193548
Adjusted R-squared
0.968292
S.D. dependent var
0.494186
S.E. of regression
0.087999
Akaike info criterion
-1.945778
Sum squared resid
0.441397
Schwarz criterion
-1.774235
Log likelihood
65.31911
F-statistic
466.6963
Durbin-Watson stat
2.019607
Prob(F-statistic)
0.000000
A raíz de los resultados de esta estimación compute la FRI (función de respuesta a un impulso) de la
inflación en la Comunidad de Andalucía a un incremento de la inflación en España 3 periodos hacia delante.
Compute también la ganancia. ¿Qué podemos decir sobre la relación dinámica entre estas dos variables?
2) Obtenemos de E-views los correlogramas del logaritmo del PIB real chileno en niveles y primeras
diferencias
PIB en niveles
PIB en primeras diferencias
También se realiza un test de raíces unitarias para la serie en niveles y primeras diferencias
obteniéndose los siguientes resultados:
Test de raíces unitarias para serie en niveles
Null Hypothesis: LPIBR has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 8 (Automatic based on SIC, MAXLAG=13)
t-Statistic
Prob.*
Augmented Dickey-Fuller test statistic
-1.764795
0.7169
Test critical values:
1% level
-4.020822
5% level
-3.440263
10% level
-3.144585
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(LPIBR)
Method: Least Squares
Date: 05/12/07 Time: 13:43
Sample (adjusted): 1967Q2 2004Q2
Included observations: 149 after adjustments
Variable
Coefficient
Std. Error
t-Statistic
Prob.
LPIBR(-1)
-0.022815
0.012928
-1.764795
0.0798
D(LPIBR(-1))
0.267903
0.078358
3.418947
0.0008
D(LPIBR(-2))
-0.005408
0.079505
-0.068019
0.9459
D(LPIBR(-3))
0.109125
0.079010
1.381149
0.1695
D(LPIBR(-4))
0.431370
0.070442
6.123770
0.0000
D(LPIBR(-5))
-0.390663
0.070313
-5.556070
0.0000
D(LPIBR(-6))
-0.101403
0.077676
-1.305472
0.1939
D(LPIBR(-7))
-0.189941
0.078146
-2.430609
0.0164
D(LPIBR(-8))
0.362063
0.077182
4.691036
0.0000
C
0.331872
0.187179
1.773018
0.0784
@TREND(1965Q1)
0.000266
0.000131
2.031125
0.0442
R-squared
0.806330
Mean dependent var
0.009757
Adjusted R-squared
0.792296
S.D. dependent var
0.048152
S.E. of regression
0.021945
Akaike info criterion
-4.729598
Sum squared resid
0.066458
Schwarz criterion
-4.507830
Log likelihood
363.3550
F-statistic
57.45532
Durbin-Watson stat
2.078309
Prob(F-statistic)
0.000000
Test de raíces unitarias para serie con una diferencia estacional
Null Hypothesis: LP has a unit root
Exogenous: Constant, Linear Trend
Lag Length: 4 (Automatic based on SIC, MAXLAG=13)
t-Statistic
Augmented Dickey-Fuller test statistic
-2.479263
Test critical values:
1% level
-4.019151
5% level
-3.439461
10% level
-3.144113
Prob.*
0.3380
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(D12LPIBR)
Method: Least Squares
Date: 05/12/07 Time: 13:48
Sample (adjusted): 1966Q2 2004Q2
Included observations: 153 after adjustments
Variable
Coefficient
Std. Error
t-Statistic
D12LPIBR(-1)
-0.006483
0.002615
-2.479263
D(D12LPIBR(-1))
0.554995
0.079008
7.024526
D(D12LPIBR(-2))
0.094506
0.091362
1.034421
D(D12LPIBR(-3))
-0.005664
0.091156
-0.062131
D(D12LPIBR(-4))
0.281881
0.078978
3.569090
C
-0.021235
0.020974
-1.012457
@TREND(1965Q1)
0.000411
0.000259
1.583685
R-squared
0.786305
Mean dependent var
Adjusted R-squared
0.777523
S.D. dependent var
S.E. of regression
0.056212
Akaike info criterion
Sum squared resid
0.461331
Schwarz criterion
Log likelihood
226.9143
F-statistic
Durbin-Watson stat
1.901881
Prob(F-statistic)
Prob.
0.0143
0.0000
0.3026
0.9505
0.0005
0.3130
0.1154
0.079751
0.119175
-2.874697
-2.736050
89.53586
0.000000
Explique e interprete los resultados obtenidos en el test.
¿Son estos resultados consistentes o contradictorios con el análisis de los correlogramas? razone su respuesta.
3) Se define el siguiente proceso VAR(1)
donde
y
son términos de error ruido blanco.
Responder a las siguientes preguntas.
a) Discuta si el sistema (1) es o no estacionario. Escriba a partir de sustituciones recursivas el
modelo (1) como función de los términos de error
en diferentes momentos del tiempo. A
raíz de esa especificación discuta qué implica la condición de estacionariedad a la hora de
explicar el efecto de estos términos de error sobre las variables endógenas del modelo.
b) Discuta de forma razonada si las variables
,
,
e
son endógenas, exógenas o
predeterminadas. ¿Qué consecuencias tiene en la estimación y la especificación del modelo?
c) Explique de que forma el sistema (1) puede recoger relaciones de contemporaneidad entre las
variables
e
.
4) Se propone el siguiente modelo VAR
donde
y
son términos de error ruido blanco.
Responder si las siguientes afirmaciones son verdaderas o falsas. Justificar brevemente.
a) El sistema (1) es estacionario si los autovalores de la matriz
son mayores que la
unidad.
b) El sistema (1) no es estacionario ya que los autovalores de la matriz
son
menores que la unidad.
c) El sistema (1) no es un modelo recursivo en general pero lo sería si la matriz de varianzas y
covarianzas de los términos de error fuera diagonal.
d) Las variables
e
son endógenas mientras la variable
es fuertemente exógena.
e) Que el proceso (1) sea estacionario implica que el efecto de los términos de error
sobre
f)
aumenta conforme i se incrementa.
Si el modelo (1) está bien especificado se debe cumplir que
.
g) Bajo el supuesto de que el modelo es correcto siempre se cumple que
para
ya que los elementos del término de error son ruido blanco por definición.
h) Se puede afirmar que en el modelo (1) no existe relación contemporánea entre sus
variables endógenas.
i)
El sistema (1) no es estacionario si los elementos del vector
son ambos mayores que
la unidad en valor absoluto.
j)
El sistema (1) se puede estimar eficientemente ecuación por ecuación ya que los
regresores son idénticos en ambas ecuaciones.
k) El sistema (1) no se puede estimar de forma consistente ecuación por ecuación ya que las
variables explicativas en las dos ecuaciones son predeterminadas.
l)
Nunca es eficiente estimar el sistema (1) ecuación por ecuación ya que los términos de
error de las dos ecuaciones podrían estar correlacionados.
5) Se ha estimado el siguiente modelo para analizar la relación dinámica entre las variables
donde las variables
y
son estacionarias y
y
:
es un ruido blanco.
a) Obtenga la FRI y la ganancia en la función de transferencia.
b) Responda verdadero a falso a las siguientes proposiciones. Justifique brevemente su respuesta.
-
La variable
responde contemporáneamente a variaciones de la variable
-
La variación de
ante un impulso de la variable
ocurrido en el período t-1 es 0.3.
-
La variación de
ante un impulso de la variable
ocurrido en el período t-1 es 0.5.
-
La variación de
ante un impulso de la variable
ocurrido en el período t-1 es 0.12.
-
La relación dinámica desde la variable
decrecimiento convergente hacia cero.
-
La relación dinámica desde la variable
6) Se ha estimado el siguiente proceso de
donde
hacia
hacia
a) ¿Es estacionario
se caracteriza por tener una fase de
es explosiva.
en función de las variables
es un proceso ruido blanco.
?
b) ¿Es estacionaria la tasa de variación de
?
.
y
:
c) Calcule (muestre) y explique las características de la función de respuesta de
variación impulso de
.
ante una
d) Calcule (muestre) y explique las características de la función de respuesta de
variación impulso de
.
ante una
7) Se dispone del logaritmo de las series del ipc de España (lesp) y del ipc de la Comunidad de Madrid
(lmad) cuyo grafico se muestra a continuación
4.65
4.60
4.55
4.50
4.45
4.40
4.35
4.30
02
03
04
05
06
LESP
07
08
09
10
11
LMAD
Se sabe además que ambas series son integradas de orden 1, es decir son estacionarias tras una
diferencia regular.
a) De acuerdo con la información proporcionada por el grafico, cree que estas dos series podrían estar
cointegradas?
Se realiza una regresión entre las dos series obteniéndose los siguientes resultados
Además se ha realizado el test de raíces unitarias a los residuos de esta última regresión obteniéndose:
b) A la vista de estos resultados, se puede aceptar que estas series están cointegradas a un nivel de
significación del 5%?
c) De acuerdo con esto, estaría justificado especificar y estimar un modelo con mecanismo corrección
del equilibrio?