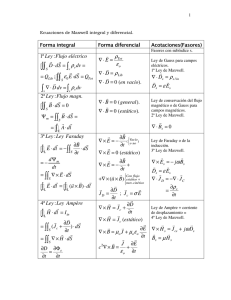
Campo eléctrico

y
La carga Q está distribuida a lo largo de un
cuarto de círculo como en figura. Halle el
campo eléctrico en el origen.
+Q
3π/4
π/4
P
x
Ey
Las contribuciones de las componentes Ex se
cancelan, el campo neto está hacia abajo en
dirección del eje y negativo.
1 λdl
1 λadθ
dq
sin(θ ) =
sin(θ ) =
sin(θ )
dE y = dE sin(θ ) =
2
2
2
4πε 0 a
4πε 0 a
4πε 0 a
1
3π / 4
1 λ
E y = ∫ dE y =
4πε 0 a
π /4
Q
2Q
λ=
=
2πa / 4 πa
3π / 4
1 λ
1 λ
3π / 4
∫π / 4sin(θ )dθ = 4πε 0 a [− cos(θ )]π / 4 = 4πε 0 a (1.414)
1
2(1.414)Q ˆ
Ey =
(− j )
2
4πε 0
πa
22.1 FLUJO ELECTRICO A TRAVES DE UN CUBO
n̂ 3
n̂ 1
n̂ 5
E
n̂ 4
n̂ 2
Se coloca un cubo de lado L en una región de
campo eléctrico uniforme E. Halle el flujo
eléctrico a través de cada cara del cubo y el
flujo total a través del cubo cuando el cubo
está orientado con dos de sus caras
perpendiculares al capo E.
n̂ 6
r
Φ E1 = Enˆ1 A = EL2 cos(180) = − EL2
r
Φ E 2 = Enˆ2 A = EL2 cos(0) = EL2
Φ E 3 = Φ E 4 = Φ E 5 = Φ E 6 = EL2 cos(90) = 0
Φ E = Φ E1 + Φ E 2 + Φ E 3 + Φ E 4 + Φ E 5 + Φ E 6 = − EL2 + EL2 = 0
LEY DE GAUSS
La ley de Gauss establece que el flujo eléctrico total a través
de cualquier superficie cerrada es proporcional a la carga
eléctrica total dentro la superficie
C. F. Gauss
n̂
Consideramos una carga puntual q adentro de una
superficie esférica imaginaria de radio R. La magnitud
del campo eléctrico es:
E=
E
q
1
q
4πε 0 R 2
El flujo eléctrico es:
Φ E = EA =
1
q
q
2
(
4
)
=
R
π
4πε 0 R 2
ε0
El flujo eléctrico no depende del radio R de la esfera, depende
únicamente de la carga q encerrada por la esfera.
Cada línea de campo que atraviesa la
esfera pequeña también atraviesa la
esfera grande, entonces el flujo total a
través de cada esfera tiene que ser lo
mismo.
E
4 dA
q
dA
El área de un elemento de superficie de
la esfera pequeña es dA. Para la esfera
grande el elemento es 4 veces mayor (el
radio es 2 veces mayor). Aunque el área
de la esfera sea mayor, el flujo es lo
mismo porque el campo eléctrico a una
distancia 2R del centro es menor:
R
2R
ΦR =
q
q
2
π
R
(
4
)
=
ε0
4πε 0 R 2
Φ2R =
1
q
q
2
π
R
(
4
(
2
)
)
=
ε0
4πε 0 (2 R) 2
1
Ese resultado es válido para una superficie de cualquier forma o tamaño, con
la sola condición de que se trate de una superficie cerrada que encierra la
carga q:
r r q
Φ E = ∫ E ⋅ dA =
ε0
q
Si la carga está afuera de la superificie
el flujo es cero:
r r
Φ E = ∫ E ⋅ dA = 0
q
Si la superficie encierra varias cargas puntuales:
n
q1
q3
q2
q4
r r
Φ E = ∫ E ⋅ dA =
∑q
i
i =1
ε0
=
Qenc
ε0
Enunciado general de la ley de Gauss
El flujo eléctrico total a través de una superficie cerrada es igual a
la carga eléctrica total presente en el interior de la superficie,
dividida entre ε0.
Qenc es siempre la suma algebraica de todas las cargas positivas y
negativas encerradas por la superficie.
La superficie imaginaria se llaman también “superficie gaussiana”
Halle el flujo eléctrico a través de la
superficie en figura, que encierra dos cargas
iguales y opuestas
-q
r r +q−q
Φ E = ∫ E ⋅ dA =
=0
ε0
+q
+q
Halle el flujo eléctrico a través de la
superficie en figura, que encierra 4 cargas
iguales, 3 positivas y una negativa:
+q
-q
+q
r r + q + q + q − q 2q
Φ E = ∫ E ⋅ dA =
=
ε0
ε0
E
φ=30o
b
σ
a
Una lámina uniformemente cargada
con densidad superficial σ=3 nC/m2
produce
un
campo
eléctrico
uniforme E horizontal. Calcule el
flujo eléctrico a través de una
superficie rectangular (a=0.02 m,
b=0.05 m) cuyo vector normal
forma un ángulo de 30o con el
campo E.
FORMULARIO
ELECTROSTÁTICA
Partículas elementales
qe = -1.6 x 10 – 19 C
me = 9.11x 10 – 31 kg.
qp = 1.6 x 10 – 19 C
mp = 1.67 x 10 – 27 kg.
qn = 0
mn = mp
qd = qp
md = 2 mp
qα = 2 qp
mα = 4 mp
Ley de Coulomb
F=
k=
4πε 0
Flujo eléctrico
F
1 q
E= =
q 4πε 0 r 2
r r
Φ E = ∫ E ⋅ dA
Densidades de carga
dq
dL
dq
σ=
dA
dq
ρ=
dV
λ=
kq1 q 2
r2
1
Campo eléctrico
Dipolo eléctrico
= 8.9 10 m / C
9
εo = 8.85x 10 –12 C2/Nm2
2
2
r
p = qd
r r
τ = p× E
r r
U = −p⋅E
A
Ley de Gauss
r r q
Φ E = ∫ E ⋅ dA =
A
ε0