Problemas Resueltos Electrostatica en el Vacio
Anuncio

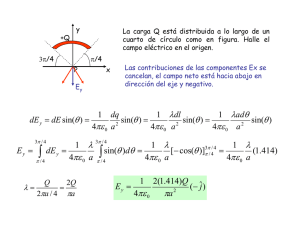
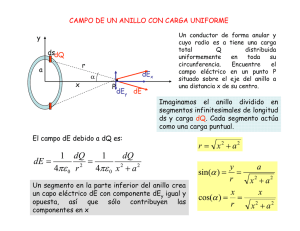
UNIVERSIDAD NACIONAL DEL CALLAO FACULTAD DE INGENIERÍA ELÉCTRICA Y ELECTRÓNICA ESCUELA PROFESIONAL DE INGENIERÍA ELÉCTRICA CURSO: TEORÍA DE CAMPOS ELECTROMAGNÉTICOS PROFESOR: Ing. JORGE MONTAÑO PISFIL PROBLEMAS RESUELTOS DE ELECTROSTÁTICA EN EL VACÍO Problema Nº 1 La distribución de una carga esférica está expresada por: ⎛ ρ0 ⎜1 − ρ= ⎝ r2 ⎞ ⎟ a2 ⎠ , r≤a , 0 r>a → a) Halle la intensidad de campo eléctrico E y el potencial eléctrico ϕ para r ≥ a → b) Halle la intensidad de campo eléctrico E y el potencial eléctrico ϕ para r ≤ a Resolución Por tratarse de una distribución esférica, hay simetría en la figura, por lo tanto la resolución de este problema puede hacerse aplicando la ley de Gauss. → a) Cálculo de E y ϕ para r ≥ a Por ley de Gauss: ρ → r a → ∫E⋅d S = dS S Q ε0 → E (4π r 2 ) = E 1 ε0 ; Q = carga neta encerrada por S.G. a 2π π ∫ ∫ ∫ r =0 φ =0 θ =0 ⎛ ρ0 ⎜1 − ⎝ r2 ⎞ 2 ⎟ r senθ dθ dφ dr a2 ⎠ → 2 ρ0 a 2 ρ0 a3 ∧ ar ; r ≥ a ⇒E= ∴ E= 15ε 0 r 2 15ε 0 r 2 3 Superficie Gaussiana (S.G.) ∫ → → Para calcular ϕ utilizamos la ecuación: ϕ = − E ⋅ d r → Reemplazando E y resolviendo luego la integral tenemos: ϕ = −∫ ∧ 2 ρ0 a 3 ∧ a ⋅ dr a r r 15ε 0 r 2 ϕ= 2 ρ0 a3 + C . . . (1) 15ε 0 r La constante C la hallo aplicando la condición de frontera (C.F.) siguiente: ϕ( r =∞ ) = 0 Si r = ∞ Evaluando en la ecuación (1) obtenemos que la constante C es igual a cero: C = 0 2 ρ0 a3 ϕ= 15ε 0 r Luego: ; para r ≥ a → b) Cálculo de E y ϕ para r ≤ a Por ley de Gauss: ρ → → ∫E⋅d S = dS S → r E (4π r 2 ) = E ⇒E= a Superficie Gaussiana (S.G.) ρ0 ε0 Q ε0 1 ε0 ; Q = carga neta encerrada por S.G. r 2π π ∫ ∫ ∫ r =0 φ =0 θ =0 ⎛ ρ0 ⎜1 − ⎝ r2 ⎞ 2 ⎟ r senθ dθ dφ dr a2 ⎠ → ⎡ r r3 ⎤ ρ0 ⎡ r r 3 ⎤ ∧ − ∴ = − E a ; r ≤a ⎢ 3 5a 2 ⎥ ε 0 ⎢⎣ 3 5a 2 ⎥⎦ r ⎣ ⎦ Hallo ϕ : ∫ → → Se cumple: ϕ = − E ⋅ d r Entonces: ϕ = −∫ ∧ ρ0 ⎡ r r 3 ⎤ ∧ ⎢ − 2 ⎥ ar ⋅ dr ar ε 0 ⎣ 3 5a ⎦ Si r = a : ϕ( r = a ) = ϕ =− ρ0 ⎡ r 2 r4 ⎤ − + C . . . (2) ε 0 ⎢⎣ 6 20a 2 ⎥⎦ ρ a2 ⎛ 1 1 ⎞ 2a 2 ρ = − 0 ⎜ − ⎟+C 15ε 0 ε 0 ⎝ 6 20 ⎠ C= a 2 ρ0 4ε 0 Reemplazando la constante C en la ecuación (2) obtenemos: ρ0 ⎡ a 2 r 2 r4 ⎤ ϕ= ⎢ − + ε 0 ⎣ 4 6 20a 2 ⎥⎦ , para r ≤ a Problema Nº 2 z Se tiene un casquete semiesférico de radio “ a ”, cargado con densidad superficial de carga constante σ y ubicado tal como se muestra en la figura. Calcule: σ a a) La intensidad de campo eléctrico en puntos sobre el eje “z”. o y b) La intensidad de campo eléctrico en el punto “o”. x Resolución: Para resolver este problema se recomienda calcular primero el potencial eléctrico, porque es más fácil resolver una integral cuyo denominador tiene potencia uno, a diferencia del exponente tres que tiene el denominador de la integral del campo eléctrico. z • P (0;0; z ) De la figura mostrada tenemos que: dA=r²senθ dθ dφ (en coordenadas esféricas) a → r − r' r donde: r = a = radio de la semiesfera. σ o θ y φ Además, por ley de cosenos se cumple: → → → → → ´ r' r − r = a 2 + z 2 − 2az cos θ x dA Cálculo del potencial eléctrico “ ϕ ” en el punto P (0; 0; z) Sabemos que para una distribución de carga superficial, el potencial eléctrico ϕ se halla por: ϕ= 1 4πε 0 ∫ σ dA → ´ → . . . (1) r−r Reemplazando dA en la ecuación (1), tenemos: ϕ= Resolviendo se obtiene: π 1 4πε 0 ϕ= 2π σ r 2 senθ dθ dφ ∫π φ∫ θ= ; donde: r = a a 2 + z 2 − 2az cos θ =0 2 ( σa a + z − a2 + z2 2ε 0 z ) → Cálculo del campo eléctrico “ E ” en el punto P (0; 0; z) Cuando ya se conoce el potencial eléctrico, el campo eléctrico se puede calcular utilizando r gradiente de potencial. Es decir, se cumple que: E = - ∇ϕ . ⎛ ∂ϕ ∧ ∂ϕ ∧ ∂ϕ ∧ ⎞ ax + ay + az ⎟ (en coordenadas cartesianas) ∂y ∂z ⎠ ⎝ ∂x Recordar también que: ∇ϕ = ⎜ r Calculando el gradiente del potencial y aplicando E = - ∇ϕ obtenemos: r σ a2 ⎛ ⎞∧ a E= 1 − ⎜ ⎟ az 2ε 0 z 2 ⎝ a2 + z2 ⎠ → Cálculo del campo eléctrico “ E ” en el punto “O” En el punto “O” (origen de coordenadas): z = 0 (Cero). → Al evaluar el campo eléctrico E en z = 0 (primero hay que levantar la indeterminación), obtenemos: → E ( z =0 ) = σ ∧ az 4ε 0 Problema Nº 3 Demostrar que el campo eléctrico en el punto (0, 0, h), debido al rectángulo descrito por −a ≤ x ≤ a ; −b ≤ y ≤ b ; z = 0 y que porta una carga uniforme de σ (C / m 2 ) es: → E= ⎛ ⎞∧ σ ab arc tg ⎜ a 2 2 2 1/ 2 ⎟ z πε 0 ⎝ h( a + b + h ) ⎠ Resolución De acuerdo con el enunciado la figura correspondiente es: z •(0;0; h) r − r' r → σ -a -b dA r' b y a x → La intensidad de campo eléctrico E se determina de manera directa utilizando la siguiente ecuación: → E= 1 4πε 0 ∫ σ dA → → ´ → → ( r − r´ ) 3 . . . (1) r−r De la figura: → → ∧ ∧ → ∧ r = h a y ; r ´ = x ax + y a y ; → r − r ´ = (h 2 + x 2 + y 2 )1/ 2 ; dA = dx ⋅ dy Reemplazamos en (1): → E= → E= σ 4πε 0 ∧ ∧ ∧ σ dx ⋅ dy (h ak − x ax − y a y ) 2 2 2 3/ 2 ∫ 4πε 0 (h + x + y ) ∧ ∧ ∧ hdx ⋅ dy xdx ⋅ dy ydx ⋅ dy a − a − a ∫∫ (h2 + x 2 + y 2 )3/ 2 z ∫∫ (h2 + x 2 + y 2 )3/ 2 x ∫∫ (h2 + x 2 + y 2 )3/ 2 y Debido a la simetría de la figura las dos últimas integrales son iguales a cero, por lo tanto la ecuación anterior queda: σh 4πε 0 → E= y =b x = a ∧ dx ⋅ dy a ∫ ∫ (h2 + x 2 + y 2 )3/ 2 z . . . (2) y =− b x =− a Pasando a coordenadas polares tenemos: x = r cos θ ; y Los límites de las integrales serán: b Para θ : 0 y arc o t g (b / a ) r θ -a y = rsenθ ; x 2 + y 2 = r 2 a * tg x b ⇒ θ = arco tg (b / a) a Para r : 0 y -b * cos θ = a sec θ a ⇒ r = a sec θ r Luego, la ecuación (2) equivale a: ⎡ σh ⎢ 8 E= 4πε 0 ⎢ → ⎣ ar co t g ( b / a ) a secθ θ =0 r =0 ∫ ∫ ⎤ rdr ⋅ dθ ∧ ⎥ az (r 2 + h 2 )3/ 2 ⎥ ⎦ Evaluando esta integral obtenemos: ⎛ ⎞ ∧ σ ab ⎟a E= arco tg ⎜ ⎜ h ( a 2 + b 2 + h 2 )1/ 2 ⎟ z πε 0 ⎝ ⎠ → , lo cual queríamos demostrar.