EJERCICIOS DE LA SEMANA (LECCIÓN 1): 1.
Anuncio

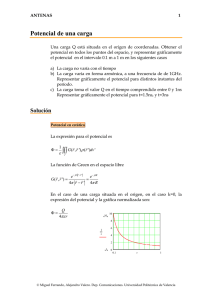
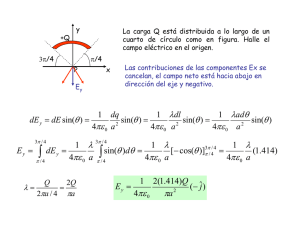
EJERCICIOS DE LA SEMANA (LECCIÓN 1): 1.- Una carga puntual positiva q, está situada en el origen de un sistema de coordenadas ortogonales sobre el plano. Otra carga puntual negativa 2q está situada sobre el eje de ordenadas positivo a una distancia de 2 m del origen. Determina: a) Intensidad del campo eléctrico creado por cada una de las cargas en un punto A situado sobre el eje OX positivo, a 1 m del origen. b) Intensidad del campo eléctrico total creado por ambas cargas en A. c) Trabajo necesario para trasladar una carga q desde el punto A a otro punto B de coordenadas (0,1) m. 2.- Una esfera no conductora tiene un hueco en su interior, siendo R su radio interior, y 2R su radio exterior. En dicha esfera está repartida, uniformemente, una carga negativa de valor 2Q. En el centro del hueco hay colocada una carga positiva Q. Suponiendo conocidos los valores de Q y R, calcular: a) La densidad volumétrica de carga de la esfera, ρ. b) El campo eléctrico en las distintas zonas del espacio r ≤ R, R ≤ r R ≤ 2R y 2R ≤ r (r es la distancia del punto considerado al centro de la esfera) (el resultado se puede expresar en función de Q, R y ρ). c) La diferencia de potencial entre un punto A situado en la superficie interior de la esfera (r = R) y otro B situado a una distancia 3R del centro. d) El trabajo que hay que hacer para llevar una carga negativa de valor 5Q desde A hasta B, indicando si ese trabajo es realizado por el campo eléctrico, o bien es necesario hacerlo en contra de las fuerzas de dicho campo eléctrico. e) ¿Es posible calcular la diferencia de potencial entre el punto B anterior y el infinito?. ¿Porqué?. Solución: 1.- r r r r r − 2q − i + 2 j − 2kq r r qr = a) E q = k 2 i = kq i V / m E − 2 q = k ( ) (− i + 2 j ) V / m 1 ( 5 )2 5 5 5 r r 2kq r r 2 r 4 r (− i + 2 j ) = kq(1 + )i − j V / m b) E = kq i − 5 5 5 5 5 5 c) ℑAB = q( VA − VB ) VA = k − 2q q 2 +k = kq(1 − )V 1 5 5 VB = k q − 2q +k = −kq V 1 1 1 )J >0 5 realizado por las fuerzas del campo ℑAB = q( VA − VB ) = 2kq 2 (1 − Por lo tanto, el trabajo es 2.a) ρ = − 2Q 4 π (8R3 − R 3 ) 3 b) R<r E4πr 2 = =− Q ε0 3 Q C / m3 3 14 πR ⇒ E(r < R) = Q 4πε 0r 2 V /m R<r<2R 4 4 Q + ρ π (r 3 − R 3 ) Q + ρπ (r 3 − R3 ) 3 3 E4πr 2 = V /m ⇒ E(R < r < 2R) = ε0 4πε 0r 2 r>2R E4πr 2 = Q − 2Q ε0 ⇒ E(r > 2R) = −Q V /m 4πε 0r 2 4 Q + πρ (r 3 − R 3 ) 3R −Q 1 Q 3 ρR 2 3 c) VA − VB = ∫ dr + dr = + V 2 2 ∫ 4 πε r 4 πε r 12 πε R 2 ε 0 0 0 0 R 2R 2R 1 Q 3 ρR 2 d) ℑAB = −5Q( VA − VB ) = −5Q( + )J <0 12 πε 0R 2 ε 0 Al ser negativo, significa que el trabajo es realizado por fuerzas externas al campo. e) Sí que es posible calcularlo, ya que: ∞ VB − V∞ = −Q ∫ 4πε r 3R 0 2 dr = − 1 Q V 12 πε 0R