PRÁCTICA Nº 2
Anuncio

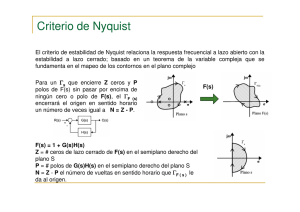
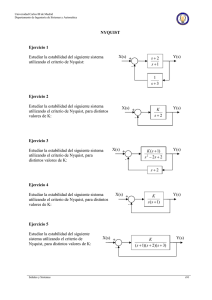
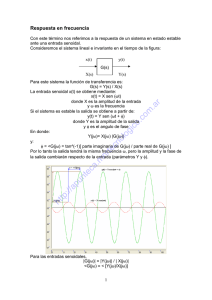
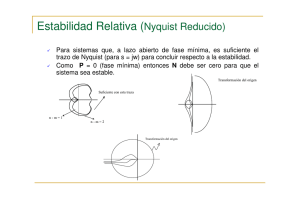
PRÁCTICA Nº 10. ANÁLISIS DE LA RESPUESTA EN FRECUENCIA UTILIZANDO MATLAB. DIAGRAMA DE NYQUIST 10. DIAGRAMA DE NYQUIST................................................................................ 1 10.1. OBJETIVOS ............................................................................................... 1 10.2. CARACTERÍSTICAS DE LA RESPUESTA EN FRECUENCIA........ 1 10.3. EJERCICIOS PROPUESTOS .................................................................. 2 Asignatura: Sistemas Lineales. Ingeniería en Automática y Electrónica Industrial. ESIDE. Área de Automática y Electrónica. Curso 2006-2007 Práctica Nº10. Diagrama de Nyquist 10. DIAGRAMA DE NYQUIST. 10.1. OBJETIVOS Familiarizarse con la representación de la función de transferencia sinusoidal en forma de diagrama polar o de Nyquist. Interpretar el diagrama de Nyquist y relacionarlo con el desarrollo teórico. Aprender a aplicar el criterio de estabilidad de Nyquist. Relacionar las especificaciones Margen de Ganancia (MG) y Margen de Fase (MF) con el diagrama polar de la función de transferencia sinusoidal de lazo abierto.. 10.2. CARACTERÍSTICAS DE LA RESPUESTA EN FRECUENCIA Basándose en el teorema de Cauchy que trata de la transformación de trayectorias en el campo complejo, el criterio de estabilidad de Nyquist analiza la estabilidad de un sistema en lazo cerrado. Para ello se apoya en la representación del diagrama polar de su función de transferencia en lazo abierto. De este modo no es necesario obtener las raíces de la ecuación característica, labor ésta muy costosa en algunos casos. En este desarrollo aparece el teorema de la transformación el cual enuncia que el número de rodeos horarios que presenta la trayectoria transformada en torno a cero es igual a la diferencia entre los ceros y polos de la función empleada en la transformación, que encierra la trayectoria original. N = Nz - Np Adaptando el anterior teorema a las necesidades del estudio de la estabilidad de un sistema, se realiza el estudio de rodeos de la trayectoria transformada en torno a menos uno, usando como función de transformación la función de transferencia en lazo abierto. La relación entre esta función y la de lazo cerrado ofrece la posibilidad de hallar los polos de esta última situados en el semiplano derecho de s. Esto se hace calculando el valor del número de ceros encerrados por la trayectoria original. Trayectoria que se tomará encerrando a todo el semiplano derecho de s. Por ello, la expresión a utilizar será, Nz = N + Np El teorema de Nyquist también permite hacer el estudio de la estabilidad relativa de un sistema mediante la modificación de las trayectorias originales. Éstas, además de recoger el semiplano derecho de s, pueden abarcar aquellas zonas en las cuales no deben ubicarse los polos del sistema, y que son definidas por especificaciones establecidas a priori. Laboratorio de Sistemas de Medida y Regulación 10-1 Sistemas Lineales. Cuaderno de Prácticas. Analizando igualmente el diagrama de Nyquist se pueden hallar valores característicos como el margen de ganancia (MG) y el margen de fase (MF). Estos parámetros se definen del siguiente modo. Margen de ganancia → La cantidad por la cual hay que multiplicar el valor en magnitud del diagrama de Nyquist, cuando éste cruza el eje real negativo, para llevarlo al límite de estabilidad (-1 + j0). MG = 1 G ( jω CF ) Esto se produce a una ω llamada frecuencia de cruce de fase (ωCF). Margen de fase → Cantidad de retraso de fase que se requiere añadir a la frecuencia de cruce por el valor de magnitud igual a uno, para llevar el sistema al borde de la inestabilidad G ( jω CG ) = 1 γ = 180º +φ Esto se produce a una ω llamada frecuencia de cruce de ganancia (ωCG). En sistemas de segundo orden, o para sistemas de orden superior con un par de polos complejos conjugados dominantes, si se da que el coeficiente de amortiguamiento es menor a 0.7 (ξ < 0.7), se puede aproximar el margen de fase por, γ = 100 · ξ 10.3. EJERCICIOS PROPUESTOS Estabilidad del sistema en lazo cerrado Se desea estudiar mediante el criterio de Nyquist, la estabilidad en lazo cerrado de un sistema dado. Con este propósito se adjunta a continuación el esquema de un sistema general. R(s) + - G(s) Y(s) H(s) 10-2 ESIDE. Departamento de Automática y Electrónica Industrial Práctica Nº10. Diagrama de Nyquist Cuestiones Sean los sistemas siguientes con funciones de transferencia de cadena directa y realimentación: a) G= K (1 + s ) (1 + 10 s ) 2 b) G= K ( s − 1) (1 + 10 s ) 2 H= c) G= K s (1 + 2 s )(1 + 3 s ) 2 H =1 d) G= K s (1 − 2 s )(1 + 3 s ) 2 H =1 H= 10 1 + 6s 10 1 + 6s Se pide para cada uno de los sistemas : 1.- Dibujar el diagrama de Nyquist del sistema en bucle abierto y estudiar la estabilidad en lazo cerrado en función de K (K > 0) mediante el criterio de estabilidad de Nyquist. 2.- Para el caso de inestabilidad, obtener el número de polos en el semiplano derecho de la función de transferencia en lazo cerrado. 3.- En los casos en que se pueda aplicar el criterio de estabilidad mediante el MF y MG, comprobarlo para K = 1. Laboratorio de Sistemas de Medida y Regulación 10-3 Sistemas Lineales. Cuaderno de Prácticas. Cuestionario a la práctica a) Rango de estabilidad: En el caso de inestabilidad, nº de polos en el SPD del sistema en L.C.: MF = b) MG = Rango de estabilidad: En el caso de inestabilidad, nº de polos en el SPD del sistema en L.C.: MF = c) MG = Rango de estabilidad: En el caso de inestabilidad, nº de polos en el SPD del sistema en L.C.: MF = d) MG = Rango de estabilidad: En el caso de inestabilidad, nº de polos en el SPD del sistema en L.C.: MF = 10-4 MG = ESIDE. Departamento de Automática y Electrónica Industrial