RESUMEN_-_Nyquist By Fabricio II
Anuncio

Respuesta en frecuencia
Con este término nos referimos a la respuesta de un sistema en estado estable
ante una entrada senoidal.
Consideremos el sistema lineal e invariante en el tiempo de la figura:
x(t)
y(t)
G(s)
X(s)
Y(s)
ht
tp
://
ap
un
te
ca
.m
nr
te
cn
ol
og
i
co
.c
om
.a
r
Para este sistema la función de transferencia es:
G(s) = Y(s) / X(s)
La entrada senoidal x(t) se obtiene mediante:
x(t) = X sen (ωt)
donde X es la amplitud de la entrada
y ω es la frecuencia
Si el sistema es estable la salida se obtiene a partir de:
y(t) = Y sen (ωt + φ)
donde Y es la amplitud de la salida
y φ es el angulo de fase
En donde:
Y(jω)= X(jω) |G(jω)|
y:
φ = <G(jω) = tan^(-1)[ parte imaginaria de G(jω) / parte real de G(jω) ]
Por lo tanto la salida tendrá la misma frecuencia ω, pero la amplitud y la fase de
la salida cambiarán respecto de la entrada (parámetros Y y φ).
Para las entradas senoidales,
|G(jω)| = |Y(jω)| / | X(jω)|
<G(jω) = < [Y(jω)/X(jω)]
1
Por lo tanto, la característica de respuesta para una entrada senoidal se
obtiene directamente de:
G(jω) = Y(jω)/X(jω)
Que es una magnitud compleja
Demostración
ht
tp
://
ap
un
te
ca
.m
nr
te
cn
ol
og
i
co
.c
om
.a
r
Dado el sistema de control de la figura anterior, si la entrada es la señal
senoidal:
x(t)= X sen (ωt)
Por Teorema de Euler:
sen (ωt) = [ e^(jωt) – e^(-jωt) ] / 2j
entonces, la Transformada de Laplace de la función seno es:
L{sen(ωt)}= 1/2j ∫ [ e^(jωt) – e^(-jωt)] * e^(-st) dt =
= 1/2j * [ 1/(s-jω) – 1/s+jω ] = en el paso siguiente multiplico
numerador y denominador por el conjugado del denominador
= 1/2j * [ (s+jω) / (s^2 + ω^2) – (s-jω) / (s^2 + ω^2)] =
= 1/2j * [ (2jω) / (s^2 + ω^2) ] =
= ω / (s^2 + ω^2)
Entonces, por linealidad de la transformada
x(s) = Xω / (s^2 + ω^2)
Dado un sistema de primer orden G(s) = y(s) / x(s) = 1 / (τs+1) tenemos
y(s) = G(s) x(s)
= Xω / [ (s^2 + ω^2) (τs+1) ]
= Xω/τ / [(s+jω)( s-jω) (s+1/τ)
y(s) = C1/( s+1/τ) + C2/(s+jω) + C3/( s-jω)
Por aplicación del método de fracciones parciales
C1 = Xωτ / [1+ω^2*τ^2]
C2 = -Xe^(-ωj)|G(jω)|/2j
C3 = Xe^(ωj)|G(jω)|/2j
y(s) = Xωτ / [1+ω^2*τ^2] / ( s+1/τ) - Xe^(-ωj)|G(jω)|/2j /(s+jω) + Xe^(ωj)|G(jω)|/2j
/( s-jω)
Aplicando Transformada de Laplace
y(t)= Xωτ / [1+ω^2*τ^2] e^(-t/τ) + X|G(jω)| * (-e^[-j(ωτ + φ)] + e^[j(ωτ + φ)] ) /2j
Por el Teorema de Euler
(-e^[-j(ωτ + φ)] + e^[j(ωτ + φ)] ) /2j = sen (ωτ + φ)
En estado estacionario, t ->∞, el primer miembro es cero y entonces:
y(t) = X|G(jω)| sen(ωτ + φ)
y(t) = X sen (ωτ + φ) / (1+ ω^2*τ^2)^(1/2)
y(t) = Y sen (ωτ + φ)
Las representaciones gráficas de las funciones de
transferencias senoidales son:
1. Las trazas de Bode
2. La traza de Nyquist
2
Diagramas de Nyquist
Un sistema de control de retroalimentación simple como el mostrado en la
figura
ht
tp
://
ap
un
te
ca
.m
nr
te
cn
ol
og
i
co
.c
om
.a
r
es estable si su Ecuación Característica a Lazo Cerrado, F(s) = 1 + G(s)H(s),
no tiene ninguna raíz con parte real positiva.
Para la estabilidad, todas las raíces de la ecuación característica
1 + G(s)H (s) = 0
deben estar en el semiplano izquierdo del plano “s”.
[Se debe señalar que, aunque los polos y ceros de la función de transferencia
en lazo abierto G(s)H(s) pueden estar en el semiplano derecho del plano “s”, el
sistema solo es estable si todos los polos de la función de transferencia en lazo
cerrado (es decir, las raíces de la ecuación característica) están en el
semiplano izquierdo del plano “s”].
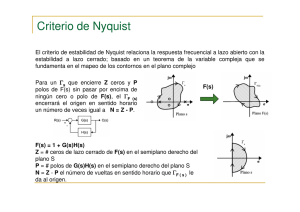
El criterio de estabilidad de Nyquist relaciona la respuesta, en el dominio de la
frecuencia, de la función de transferencia en lazo abierto G(jw)H(jw) con el
número de ceros (Z) y polos (P) de 1 + G(s)H(s) que se encuentran en el
semiplano derecho del plano “s”.
El criterio de estabilidad de Nyquist relaciona la respuesta frecuencial a lazo
abierto con la estabilidad a lazo cerrado; basado en la representación en
coordenadas polares. El criterio está basado en un teorema de la teoría de las
variables complejas que requiere realizar un mapeo del plano s al plano G(s)
para entenderlo.
El diagrama polar de una función de transferencia sinusoidal G(jw) es una
gráfica de la magnitud de G(jw) con respecto al ángulo de fase de G(jw) en
coordenadas polares, cuando “w” varía de cero a infinito. Por tanto, el diagrama
polar es el lugar geométrico de los vectores |G( jw)|<G( jw) cuando “w” varía de
cero a infinito. Las proyecciones de G(jw) en los ejes real e imaginario son sus
componentes real e imaginaria. En las gráficas polares, los ángulos de fase son
positivos (negativos) si se miden en el sentido contrario al de las agujas del
reloj (en el sentido de las agujas) a partir del eje real positivo. El diagrama polar
se denomina, a menudo, “Diagrama de Nyquist”.
3
Ventajas de los diagramas de Nyquist
• Representa, en una sola gráfica, las características de la respuesta, en
el dominio de la frecuencia, de un sistema en el rango de frecuencia
completo.
• Determina gráficamente de las curvas de respuesta de lazo abierto la
estabilidad absoluta del sistema de lazo cerrado, sin necesidad de
determinar los polos de lazo cerrado.
Una desventaja
• No indica en forma clara la contribución de todos los factores
individuales de la función de transferencia en lazo abierto.
.a
r
Trayectoria de Nyquist
ht
tp
://
ap
un
te
ca
.m
nr
te
cn
ol
og
i
co
.c
om
Es el lugar geométrico con sentido contrario a las agujas del reloj que encierra
el semiplano derecho del plano s por completo
En la aplicación del criterio de Nyquist, el lugar geométrico en el plano s es la
trayectoria de Nyquist. Es decir, la trayectoria de Nyquist son los valores que
toma s al mapear 1+G(s)H(s).
4
Enunciado del Criterio de estabilidad de Nyquist
nr
te
cn
ol
og
i
co
.c
om
.a
r
Si la trayectoria de Nyquist en el plano “s” encierra Z ceros y P polos de 1 +
G(s)H(s) y no pasa por los polos ni los ceros de 1 + G(s)H(s) conforme un
punto representativo “s” se mueve en el sentido de las agujas del reloj a lo
largo de la trayectoria de Nyquist, el contorno correspondiente en el plano
G(s)H(s) rodea en un círculo N = Z – P veces el punto -1 + j0 en el sentido de
las agujas del reloj. (Los valores negativos de N implican rodeos en sentido
contrario al de las agujas del reloj)
Al examinar la estabilidad de los sistemas de control lineales mediante el
criterio de estabilidad de Nyquist, se observa que se pueden presentar tres
casos:
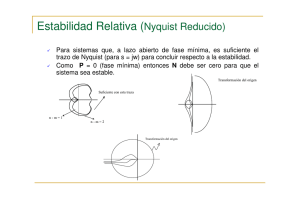
1. El punto -1 + j0 no está rodeado. Esto implica que el sistema es estable si no
hay polos de G(s)H(s) en el semiplano derecho del plano “s”; de lo contrario, el
sistema es inestable.
2. El punto -1 + j0 queda rodeado una o varias veces en sentido contrario al de
las agujas del reloj. En este caso, el sistema es estable si el número de rodeos
en sentido contrario al de las agujas del reloj es igual al número de polos
G(s)H(s) en el semiplano derecho del plano “s”; de lo contrario, el sistema es
inestable.
3. El punto -1 + j0 queda rodeado una o varias veces en el sentido de las
agujas del reloj. En este caso el sistema es inestable.
ht
tp
://
ap
un
te
ca
.m
Cabe aclarar que el criterio se aplica sobre un punto crítico, que es el punto de
origen del plano que se grafica. Para nuestro caso, el punto crítico de
1+G(s)H(S) corresponde al punto -1 + j0 en el plano G(s)H(S). Es decir, el
plano que dibujamos en el diagrama de Nyquist es el de la FTLA (G(s)H(s))
pero como concluimos sobre la FTLC no podemos tomar el origen (0,0) como
punto crítico para aplicar el criterio, sino que tomamos el punto -1 + j0 porque
es el punto crítico correspondiente al plano 1+G(s)H(S).
5
Margen de fase y Margen de ganancia
Entre más se acerca el lugar geométrico G(jw) a encerrar al punto -1+ j0, más
oscilatoria es la respuesta del sistema. Esta proximidad se utiliza como medida
del margen de estabilidad y se expresa en términos de:
ht
tp
://
ap
un
te
ca
.m
nr
te
cn
ol
og
i
co
.c
om
.a
r
1. Margen de fase γ: es la cantidad de atraso de fase adicional en la
frecuencia de cruce de ganancia requerida para llevar el sistema al
borde de la inestabilidad. La frecuencia de cruce de ganancia es la
frecuencia en la cual |G(jw)| (magnitud de la FTLA) es unitaria.
γ = 180º + φ
2. Margen de ganancia Kg: es el recíproco de la magnitud |G(jw)|, en la
frecuencia a la cual el ángulo de fase es -180º.
Kg = 1 / |G(jw)|
Para un sistema estable de fase mínima, el margen de ganancia Kg
indica cuánto puede incrementarse la ganancia antes que el sistema se
vuelva inestable. Para un sistema inestable, el margen de ganancia Kg
indica cuánto debe disminuir la ganancia para que el sistema se vuelva
estable.
Para sistemas de primer y segundo orden, el margen de ganancia Kg es
infinito, dado que las trazas polares para tales sistemas no cruza el eje
real negativo. Por lo tanto tales sistemas no pueden ser inestables.
Para un sistema de fase no mínima con un lazo abierto inestable, la
condición de estabilidad no se satisface a menos que la gráfica G(jw)
encierre al punto -1+j0, por lo tanto, tendrá márgenes de fase y de
ganancia negativos.
6
7
ht
.m
ca
un
te
ap
://
tp
.c
co
nr
te
cn
ol
og
i
om
.a
r