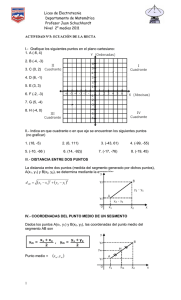
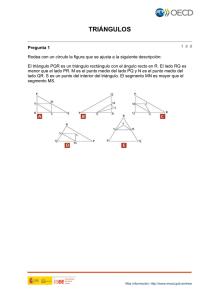
Guía Teorema de Thales y división de segmentos
Anuncio

PROGRAMA EGRESADOS GUICEG029EM32-A16V1 Ejercicios PSU 1. Un punto R divide interiormente al trazo PQ en la razón 4 : 7. Si PR = 28 cm, entonces ¿cuánto mide el segmento PQ? A) B) C) D) E) 2. Dos segmentos están en la razón 1 : 3. ¿En qué razón quedarán si el segmento mayor es reducido a la mitad? A) B) C) D) E) 3. En la figura, el punto D divide al segmento AB en la razón 3 : 5. Si DB = 40 cm, ¿cuánto mide AB ? Matemática Guía: Teorema de Thales y división de segmentos 77 cm 65 cm 49 cm 44 cm 16 cm 1:1 1:3 2:3 3:2 Ninguna de las razones anteriores. A) 106,6 cm B) 66,6 cm C) 64 cm D) 24 cm E) A D B Ninguna de las medidas anteriores. Cpech 1 Matemática 4. El segmento AB se divide interiormente en la razón 2 : 3 : 4. Si el segmento menor mide 18 cm, ¿cuánto mide el segmento AB? A) B) C) D) E) 5. En la figura, R divide al segmento PQ en la razón 6 : 11. Si RQ = 55 cm, ¿cuánto mide PQ ? A) 30 cm B) 85 cm 9 cm 27 cm 36 cm 81 cm Faltan datos para determinarlo. C) 100,83 cm D) 155,83cm P E) Ninguna de las medidas anteriores. 6. En el triángulo ABC de la figura, AD = m, DB = n y BC = a. El segmento AC es C an A) m 30º am B) n mn C) a n D) am m E) an 2 Q R Cpech A 40º 80º D B Guía 7. En el triángulo ABC de la figura, BD es bisectriz del ángulo CBA. Si AC = 10 cm, entonces el segmento AD mide C 20 A) cm 7 50 B) cm 11 5 cm D 60 C) cm 11 50 D) cm 7 A B 6 cm E) ninguna de las medidas anteriores. 8. En el triángulo PQR de la figura, PS es bisectriz del ángulo QPR. Si RQ = 3, entonces el segmento RS es igual a R A) 3(m – 1) 2m B) 3m m+1 3(m + 1) C) m–1 3(m + 1) D) 2m 3(m – 1) E) m+1 9. En la figura, L1 // L2 // L3. El valor del segmento AB es A) 2 B) 2,6 C) 9,3 D)24 E) ninguno de los valores anteriores. m+1 P Q m–1 A L1 B L2 L3 S C L4 8 D 5 E 15 F L5 Cpech 3 Matemática 10. En el triángulo ABE de la figura, ABCD es un trapecio. ¿Cuál es el valor de AD ? E A)35 7 B)31 C)28 D)11 E) 4 D Faltan datos para determinarlo. A C B 20 11. En la figura, L1 // L2. Si AB = 4 cm, OC = 6 cm y OB = 2 cm, ¿cuánto mide CD ? A) 12 cm B) 4 cm C) 3 cm D) E) A L1 B O L2 4 cm 3 D C L3 Ninguna de las medidas anteriores. L4 12. En la figura, E es el punto de intersección entre BC y AD . Si AB // CD, ¿cuál es el valor de AE? D B A)45 30 B)35 C)25 E 10 15 D)20 E) 5 A C 13. En la figura, AB = BC = CD = DE = EF = 2 cm y EG = 3 cm. ¿Cuánto mide AH ? 4 A) 5,3 cm B) 6,6 cm C) 9 cm D) 12 cm E) 15 cm Cpech H G A B C D E F Guía 14. En el trapecio ABCD de la figura, E y F son puntos medios de AD y BC , respectivamente. Si BG = 12 cm, FG = 6�3 cm y EG = �6 cm, ¿cuánto mide AG ? B)12�2 cm C) 9�2 cm D) 2�2 cm E) 1,5�2 cm C D A)36�2 cm E F a G a B A 15. En el triángulo ABC de la figura, AC = m y BC = p, entonces p es igual a A) mq n B) nq m C) mq m–n C q D A 70º E n 70º B m D) (m – n)q (m – n)q E) m 16. En el triángulo ABC de la figura, FG // DE // CB y FG = 8 cm. Si AF : FD : DC = 3 : 2 : 5, la medida de BC es 56 A) cm 3 B E 80 B) cm 3 C) G A 40 cm D) 80 cm E) ninguna de las medidas anteriores. F D C Cpech 5 Matemática 17. En el triángulo ABC de la figura, ED // CB. Si DB = x + 6 y AB = 3x + 6, entonces la medida de AD es C A) 1 metro. B) 2 metros. C) 4 metros. D) 8 metros. E) 12 metros. E 12 m 4m A B D 18. Un poste perpendicular al suelo que mide 2,5 metros proyecta una sombra de 5 metros de largo. Si a esa misma hora y en ese mismo lugar, una casa proyecta una sombra de 9 metros, ¿cuál es la altura de la casa? A) B) C) D) E) 4,5 metros 5,5 metros 6,5 metros 7,5 metros 18 metros 19. En el triángulo ABC de la figura, AC // DE. Si BE = 12, EC = 18 y AB = 40, entonces el valor de AD es C A) 8 B) 9 C)16 D)24 E) ninguno de los valores anteriores. E A 6 Cpech D B Guía 20. En la figura, el triángulo PQR es isósceles en R, RP // TM, RQ // TN , PM = 2 y TS = 3. Si PM : MS = 1 : 2, entonces ¿cuál es el valor de RP ? A) 7,5 B) 2,5 R T 3�10 C) 4 P M �10 D) 2 E) S N Q Faltan datos para determinarlo. 21. Un edificio que proyecta una sombra de 15 metros, está a 5 metros de otro edificio de 12 metros de altura, como muestra la figura. ¿Cuál es la altura x del edificio? A) B) C) D) E) 6 metros 8,3 metros 12,5 metros 15 metros 18 metros x 12 m a 5m 15 m 22. En un mismo plano horizontal, a la misma hora y en el mismo lugar, las sombras de un niño y un árbol miden 0,72 metros y 20 metros respectivamente. Si la altura del niño es de 1,08 metros, ¿cuál es la altura del árbol? A) B) C) D) E) 30 metros 29,58 metros 28,92 metros 28,5 metros Ninguna de las medidas anteriores. Cpech 7 Matemática 23. ¿En cuál(es) de las siguientes figuras el valor de x es 30°? I) L2 L3 II)L3 L1 15 7 14 L4 A) B) C) D) E) x L1 x L4 III) L2 x 24 10 45 12 L1 // L2 30 20 L2 L5 L1 // L2 // L3 L1 L4 L3 L1 // L2 Solo en I Solo en II Solo en III Solo en I y en II En I, en II y en III 24. En la figura, AB = 26 cm, se puede determinar la medida del segmento AD si: (1) AD : DB = 6 : 7 DB es el segmento mayor. (2) A)(1) por sí sola. B) (2) por sí sola. C) Ambas juntas, (1) y (2). D) Cada una por sí sola, (1) ó (2). E) Se requiere información adicional. A B D 25. En la figura, es posible determinar que Δ AOC ~ Δ DOB, si: (1) α = β (2) OB = OD = 2 cm. A) B) C) D) E) a (1) por sí sola. (2) por sí sola. Ambas juntas, (1) y (2). Cada una por sí sola, (1) ó (2). Se requiere información adicional. Cpech b L1 O B L3 8 C A D L2 L4 Guía Tabla de corrección Ítem Alternativa Habilidad 1 Aplicación 2 Comprensión 3 Aplicación 4 Aplicación 5 Aplicación 6 Aplicación 7 Aplicación 8 Aplicación 9 Aplicación 10 Aplicación 11 Aplicación 12 Aplicación 13 Aplicación 14 ASE 15 Aplicación 16 ASE 17 Aplicación 18 ASE 19 Aplicación 20 ASE 21 Aplicación 22 ASE 23 Aplicación 24 ASE 25 ASE Cpech 9 Matemática Mis apuntes 10 Cpech Guía Mis apuntes Cpech 11 Registro de propiedad intelectual de Cpech. Prohibida su reproducción total o parcial.