Guía de Matemáticas: Números Reales y Fracciones
Anuncio
PR
A EG RE
SA
S
DO
RAM
G
O
Guía
Retroalimentación 1
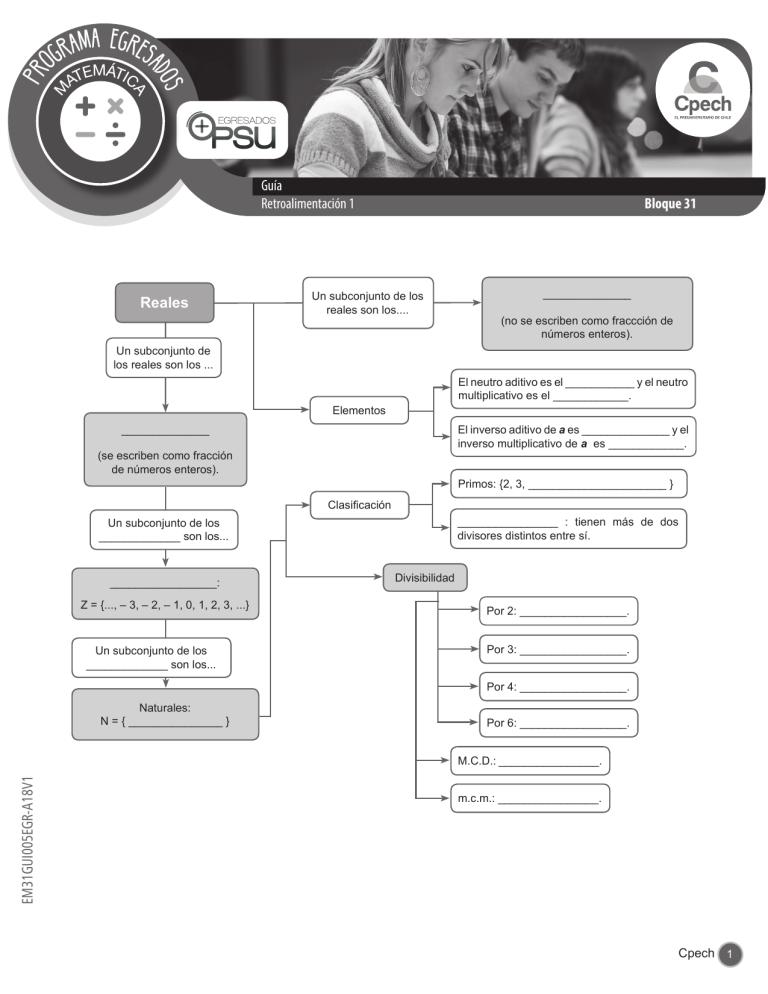
Reales
Bloque 31
Un subconjunto de los
reales son los....
______________
(no se escriben como fraccción de
números enteros).
Un subconjunto de
los reales son los ...
El neutro aditivo es el ___________ y el neutro
multiplicativo es el ____________.
Elementos
El inverso aditivo de a es ______________ y el
inverso multiplicativo de a es ____________.
______________
(se escriben como fracción
de números enteros).
Primos: {2, 3, ______________________ }
Clasificación
________________ : tienen más de dos
divisores distintos entre sí.
Un subconjunto de los
_____________ son los...
_________________:
Z = {..., – 3, – 2, – 1, 0, 1, 2, 3, ...}
Un subconjunto de los
_____________ son los...
Divisibilidad
Por 2: _________________.
Por 3: _________________.
Por 4: _________________.
Naturales:
N = { _______________ }
Por 6: _________________.
EM31GUI005EGR-A18V1
M.C.D.: ________________.
m.c.m.: ________________.
Cpech 1
MATEMÁTICA
Se igualan
____________ y
se comparan los
numeradores.
Orden
¿Cómo ordenar
con fracciones?
¿Cómo representar
un número con
muchos decimales?
Por ejemplo,
aproximando
a la décima
2,6 = 2,7
2,3 = 2,3
2,6 = 2,6
2,3 = 2,3
2,6 = 2,7
2,3 = 2,4
Aproximación
______________
5=
____________
3,7 =
____________
____________
Operatoria
División
Igual
denominador
Distinto
denominador
5
3
7 + 7 =
4
9
–
=
13 13
7
5
4 + 6 =
4 2
– =
5 3
3 6
• =
5 7
–8 2
• =
5 9
3 2 3 7
5:7=5·2=
–5 –2
–5 3
4 : 3 = 4 ·–2=
37
10
5,6 =
2,56 =
56 – 5 51
=
9
9
256 – 25 231
=
90
90
___________: multiplicar numerador
y denominador por el mismo número.
2
10
2•5
=
=
3
15
3•5
____________: dividir numerador y
denominador por el mismo número.
12
2
12 : 6
=
=
30
5
30 : 6
______________
Multiplicación
Cpech
¿Cómo operar
con fracciones?
______________
Adición y
sustracción
2
Racionales
¿Qué
números
se pueden
escribir como
fracción de
enteros?
5
1
____________
Regla de los signos
Al sumar dos números de igual signo, se
mantiene el signo. Al sumar dos números
de distinto signo, se mantiene el signo del
que tenga mayor valor absoluto.
La resta de dos números se puede escribir
como una suma (a – b = a + (–b)). Luego
se aplican propiedades de la suma.
(+) • (+) =
(–) • (–) =
(+) • (–) =
(–) • (+) =
Guía
Nivel 1
1.
¿Cuál(es) de las siguientes afirmaciones es (son) siempre verdadera(s)?
I)
La suma entre números enteros resulta un número entero.
II)
La sustracción no es conmutativa en los números naturales.
III) En los números naturales, el inverso aditivo de 3 es – 3.
A)
B)
C)
D)
E)
2.
3.
Se puede concluir que p es un número real positivo, si:
(1)
(2)
3p es positivo.
(p – 5) es negativo.
A)
B)
C)
D)
E)
(1) por sí sola.
(2) por sí sola.
Ambas juntas, (1) y (2).
Cada una por sí sola, (1) ó (2).
Se requiere información adicional.
Sea n el número real positivo que es igual a su inverso multiplicativo y m el número real que es
igual a su inverso aditivo. Los números n y m son, respectivamente,
A)
B)
C)
D)
E)
4.
Solo I
Solo II
Solo III
Solo I y II
Solo I y III
0y0
0y1
1y1
1y0
2y1
¿Cuál(es) de las siguientes afirmaciones es (son) siempre verdadera(s)?
I)
El inverso multiplicativo de un número entero distinto de cero es un número racional.
II)
Los elementos neutros en la adición y la multiplicación son 0 y 1, respectivamente.
III) El inverso multiplicativo de una fracción propia se puede representar como una fracción
mixta.
A)
B)
C)
D)
E)
Solo I
Solo II
Solo III
Solo I y II
I, II y III
Cpech
3
MATEMÁTICA
5.
La suma de cuatro números primos es 96. ¿Cuál es el máximo común divisor entre ellos?
A)
B)
C)
D)
E)
6.
En un jardín infantil se necesita armar cajitas que contengan chocolates, paquetes de galletas y
caramelos. Si cuentan con 100 caramelos, 75 chocolates y 50 paquetes de galletas, ¿cuántas
cajitas se pueden armar de manera que contengan la misma cantidad de caramelos, chocolates
y paquetes de galletas?
A)
B)
C)
D)
E)
7.
0
1
224.257
No tiene.
Faltan datos para determinarlo.
300
75
25
20
15
La suma de cuatro números enteros consecutivos es siempre
I)
II)
III)
divisible por 2.
divisible por 4.
divisible por 6.
Es (son) verdadera(s)
A)
B)
C)
D)
E)
4
Cpech
solo I.
solo II.
solo I y II.
solo I y III.
solo II y III.
Guía
8.
9.
10.
4
se le aumenta en una unidad tanto su numerador como su denominador,
5
entonces la fracción resultante es
Si a la fracción
A)
menor que
4
en 1.
5
B)
menor que
4
1
en
.
5
30
C)
equivalente a
D)
mayor que
4
1
en
.
5
30
E)
mayor que
4
en 1.
5
4
.
5
En un curso de 42 alumnos, faltaron 14 de ellos. ¿Cuál(es) de las siguientes afirmaciones es
(son) verdadera(s)?
I)
Los alumnos presentes representan el doble de los ausentes.
II)
Los alumnos ausentes representan la tercera parte del curso.
III)
2
de los alumnos del curso están presentes.
3
A)
B)
C)
D)
E)
Solo III
Solo I y II
Solo I y III
Solo II y III
I, II y III
2
1
=
3
A)
1,6
B)
2,3
C)
0,16
D)
0,6
E)
2,6
Cpech
5
MATEMÁTICA
Nivel 2
11.
¿Cuál(es) de los siguientes números es (son) racional(es)?
I)
– 0,205
II)
0,123
III)
3,01
A)
B)
C)
D)
E)
12.
13.
¿Cuál(es) de las siguientes afirmaciones es (son) verdadera(s)?
I)
En los números enteros, la sustracción es conmutativa.
II)
En los números enteros, el inverso multiplicativo de 5 es
III)
1
.
5
En el conjunto de los números enteros, el neutro aditivo es el cero.
A)
B)
C)
D)
E)
Solo I
Solo II
Solo III
Solo II y III
Ninguna de ellas.
Si al antecesor de (– 5) se le suma el sucesor del doble de 3 resulta
A)
B)
C)
D)
E)
14.
Cpech
0
1
2
3
4
El largo, el ancho y el alto de un paralelepípedo corresponden a tres números pares consecutivos.
Si n es un número impar positivo y el volumen de un paralelepípedo es igual al producto entre su
largo, ancho y alto, ¿cuál de las siguientes expresiones podría representar dicho volumen?
A)
B)
C)
D)
E)
6
Solo I
Solo I y II
Solo II y III
I, II y III
Ninguno de los valores anteriores
(n + 2)(n + 4)(n + 6)
(n + 1)(n + 3)(n + 5)
(2n)(2n + 1)(2n + 2)
(2n + 1)(2n + 3)(2n + 5)
Ninguna de las expresiones anteriores.
Guía
15.
16.
¿Cuál(es) de las siguientes afirmaciones es (son) verdadera(s)? I)
II)
III)
Los números 13, 17, 19 y 23 son números primos.
El mínimo común múltiplo entre 29, 13 y 11 es el producto entre 29, 13 y 11.
El máximo común divisor entre 2, 7 y 11 es 1.
A)
B)
C)
D)
E)
Solo I
Solo II
Solo I y II
Solo I y III
I, II y III
Tres ciclistas tardan 10, 12 y 15 segundos, respectivamente, en dar vuelta completa al velódromo.
¿Al cabo de cuántos minutos se encontrarán por primera vez los tres ciclistas en el punto de
partida, si se mantienen a velocidad constante?
A)
B)
C)
D)
E)
17.
18.
60
3
2
1
Nunca se encuentran.
Sean a y b dos números enteros positivos. Se puede determinar el máximo común divisor entre
ellos si:
(1)
(2)
a y b son números pares consecutivos.
La suma entre a y b es 30.
A)
B)
C)
D)
E)
(1) por sí sola.
(2) por sí sola.
Ambas juntas, (1) y (2).
Cada una por sí sola, (1) ó (2).
Se requiere información adicional.
¿Cuál de los siguientes valores se encuentra más cercano al cero en la recta numérica?
A)
– 10
33
B)
3
10
C)
–8
25
D)
7
20
E)
1
3
Cpech
7
MATEMÁTICA
19.
1
El valor de 1 +
1+
1+
20.
8
Cpech
A)
18
11
B)
3
2
C)
1
D)
8
11
E)
7
11
70
1
+ 0,69 :
=
100
3
A)
17
7
B)
2
3
C)
4
3
D)
1
2
E)
27
21
es
1
9
12
Guía
Nivel 3
21.
Sea a un número entero y b un número racional NO entero. ¿Cuál(es) de las siguientes
operaciones siempre da(n) como resultado un número racional NO entero?
I)
a+b
II)
a·b
a
b
III)
A)
B)
C)
D)
E)
22.
Sean P y Q dos números racionales. ¿Cuál(es) de las siguientes expresiones representa(n)
siempre un número racional?
I)
P(P + Q)
II)
P2 – Q2
P
Q
III)
A)
B)
C)
D)
E)
23.
Solo I
Solo I y II
Solo II y III
I, II y III
Ninguna de ellas.
Solo I
Solo III
Solo I y II
I, II y III
Ninguna de ellas.
¿Cuál(es) de las siguientes afirmaciones es (son) verdadera(s)?
I)
II)
–3
4
es
.
4
3
1
– 16
El inverso aditivo de 5
es
.
3
3
El inverso multiplicativo de
III)
0,36 + 0,64 = 1
A)
B)
C)
D)
E)
Solo I
Solo II
Solo I y II
Solo II y III
I, II y III
Cpech
9
MATEMÁTICA
24.
25.
Se define la operación φ(n) como el producto entre n y su inverso aditivo, sumado al inverso
multiplicativo de n. ¿Cuál es el valor de φ(4)?
A)
–3
B)
– 63
4
C)
–3
4
D)
– 65
4
E)
– 15
Carmen, Patricio y Jorge tienen una caja con veinte fichas numeradas del 1 al 20. Primero,
Carmen saca todos los números múltiplos de 3 que hay en la caja, sin devolverlos. Luego, Patricio
saca todos los números primos que quedan en la caja, sin devolverlos. Finalmente, Jorge saca
todos los números que quedan en la caja. Al terminar, es correcto afirmar que
A)
B)
C)
D)
E)
26.
Si las alarmas de dos relojes están programadas para sonar cada 15 y 20 minutos
respectivamente, ¿a qué hora volverán a sonar juntos si coincidieron sus alarmas a las 8:35
horas?
A)
B)
C)
D)
E)
27.
10 Cpech
Jorge tiene la mayor cantidad de fichas.
Patricio tiene la mayor cantidad de fichas.
Patricio y Jorge tienen igual cantidad de fichas, superando ambos a Carmen.
Carmen y Jorge tienen igual cantidad de fichas, superando ambos a Patricio.
Carmen y Patricio tienen igual cantidad de fichas, superando ambos a Jorge.
8:40
8:52
9:35
13:00
13:25
M y N son dos números primos, tal que N < M. Se puede determinar el valor numérico de M, si:
(1)
(2)
(M + N) es un número primo.
(M • N) es un número par.
A)
B)
C)
D)
E)
(1) por sí sola.
(2) por sí sola.
Ambas juntas, (1) y (2).
Cada una por sí sola, (1) ó (2).
Se requiere información adicional.
Guía
28.
El orden creciente de los números a =
A)
B)
C)
D)
E)
29.
a, b, c
b, c, a
c, b, a
a, c, b
c, a, b
¿Cuál(es) de las siguientes igualdades es (son) verdadera(s)?
I)
II)
III)
A)
B)
C)
D)
E)
30.
7
8
880
,b=
yc=
es
8
9
999
70
9
52
3,46 =
15
7
= 0,63
11
7,9 =
Solo I
Solo II
Solo III
Solo II y III
I, II y III
Un vuelo desde Santiago a Buenos Aires realiza una escala de dos horas en Mendoza. Si el vuelo
3
desde Santiago a Mendoza dura 1 hora y 15 minutos, y es equivalente a los
del tiempo de vuelo
4
desde Mendoza a Buenos Aires, ¿cuál(es) de las siguientes afirmaciones es (son) verdadera(s)?
I)
El vuelo desde Santiago a Buenos Aires, considerando la escala, tiene una duración total
11
de 4
horas.
12
II)
El vuelo desde Mendoza a Buenos Aires dura 40 minutos menos que la escala realizada en
Mendoza.
III)
El vuelo desde Mendoza a Buenos Aires dura 25 minutos más que el vuelo de Santiago a
Mendoza.
A)
B)
C)
D)
E)
Solo I
Solo III
Solo I y II
Solo I y III
Solo II y III
Cpech 11
MATEMÁTICA
Tabla de corrección
Ítem
12 Cpech
Alternativa
Habilidad
Dificultad estimada
1
ASE
Fácil
2
ASE
Fácil
3
Comprensión
Fácil
4
Comprensión
Fácil
5
Comprensión
Fácil
6
ASE
Fácil
7
ASE
Fácil
8
ASE
Fácil
9
Comprensión
Fácil
10
Comprensión
Fácil
11
Comprensión
Media
12
ASE
Media
13
Aplicación
Media
14
ASE
Media
15
ASE
Media
16
ASE
Media
17
ASE
Media
18
Comprensión
Media
19
Aplicación
Media
20
Aplicación
Media
21
ASE
Difícil
22
ASE
Difícil
23
Comprensión
Difícil
24
ASE
Difícil
25
Aplicación
Difícil
26
ASE
Difícil
27
ASE
Difícil
28
ASE
Difícil
29
Comprensión
Difícil
30
ASE
Difícil
Guía
Mis apuntes
Cpech 13
MATEMÁTICA
Mis apuntes
14 Cpech
Guía
Mis apuntes
Cpech 15
_____________________________________________________
Han colaborado en esta edición:
Directora de Desarrollo Académico e Innovación Institucional
Katherine González Terceros
Coordinadora PSU
Francisca Carrasco Fuenzalida
Equipo Editorial
Rodrigo Cortés Ramírez
Pablo Echeverría Silva
Marcelo Gajardo Vargas
Andrés Grandón Guzmán
Equipo Gráfico y Diagramación
Cynthia Ahumada Pérez
Daniel Henríquez Fuentes
Vania Muñoz Díaz
Tania Muñoz Romero
Elizabeth Rojas Alarcón
Equipo de Corrección Idiomática
Paula Santander Aguirre
Imágenes
Banco Archivo Cpech
El grupo Editorial Cpech ha puesto su esfuerzo en
obtener los permisos correspondientes para utilizar las
distintas obras con copyright que aparecen en esta
publicación. En caso de presentarse alguna omisión
o error, será enmendado en las siguientes ediciones
a través de las inclusiones o correcciones necesarias.
Registro de propiedad intelectual de Cpech.
Prohibida su reproducción total o parcial.