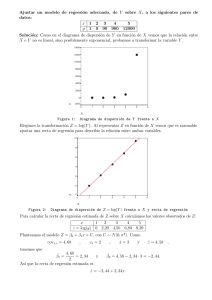
3.6.1. Bondad de un ajuste
Anuncio
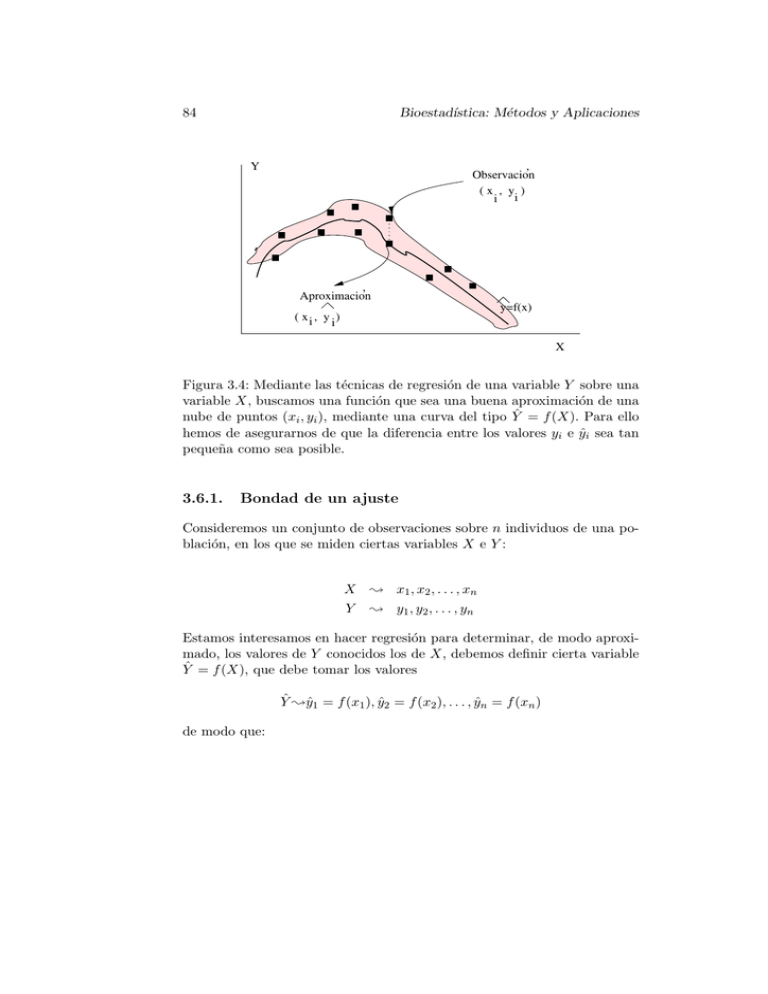
84 Bioestadı́stica: Métodos y Aplicaciones Y , Observacion (x , y ) i i , Aproximacion ( x i , y i) y=f(x) X Figura 3.4: Mediante las técnicas de regresión de una variable Y sobre una variable X, buscamos una función que sea una buena aproximación de una nube de puntos (xi , yi ), mediante una curva del tipo Ŷ = f (X). Para ello hemos de asegurarnos de que la diferencia entre los valores yi e ŷi sea tan pequeña como sea posible. 3.6.1. Bondad de un ajuste Consideremos un conjunto de observaciones sobre n individuos de una población, en los que se miden ciertas variables X e Y : X ; x1 , x2 , . . . , xn Y ; y1 , y 2 , . . . , y n Estamos interesamos en hacer regresión para determinar, de modo aproximado, los valores de Y conocidos los de X, debemos definir cierta variable Ŷ = f (X), que debe tomar los valores Ŷ ;ŷ1 = f (x1 ), ŷ2 = f (x2 ), . . . , ŷn = f (xn ) de modo que: 3.6. REGRESIÓN Modelo lineal Buen ajuste 85 Modelo lineal Mal ajuste Modelo no lineal Buen ajuste Cuando x crece, y crece Cuando x crece, y crece Modelo lineal Buen ajuste Cuando x crece, y decrece Cuando x crece, y crece Modelo no lineal Buen ajuste Variables no relacionadas Ninguna curva de regresion es adecuada Cuando x crece, y decrece Figura 3.5: Diferentes nubes de puntos y modelos de regresión para ellas. Y − Ŷ ;y1 − ŷ1 ≈ 0, y2 − ŷ2 ≈ 0, . . . , yn − ŷn ≈ 0 Ello se puede expresar definiendo una nueva variable E que mida las diferencias entre los auténticos valores de Y y los teóricos suministrados por la regresión, E = Y − Ŷ ;e1 = y1 − ŷ1 , e2 = y2 − ŷ2 , . . . , en = yn − ŷn y calculando Ŷ de modo que E tome valores cercanos a 0. Dicho de otro modo, E debe ser una variable cuya media debe ser 0 , y cuya varianza SE2 debe ser pequeña (en comparación con la de Y ). Por ello se define el