Ajustar un modelo de regresión adecuado, de Y sobre X, a los
Anuncio
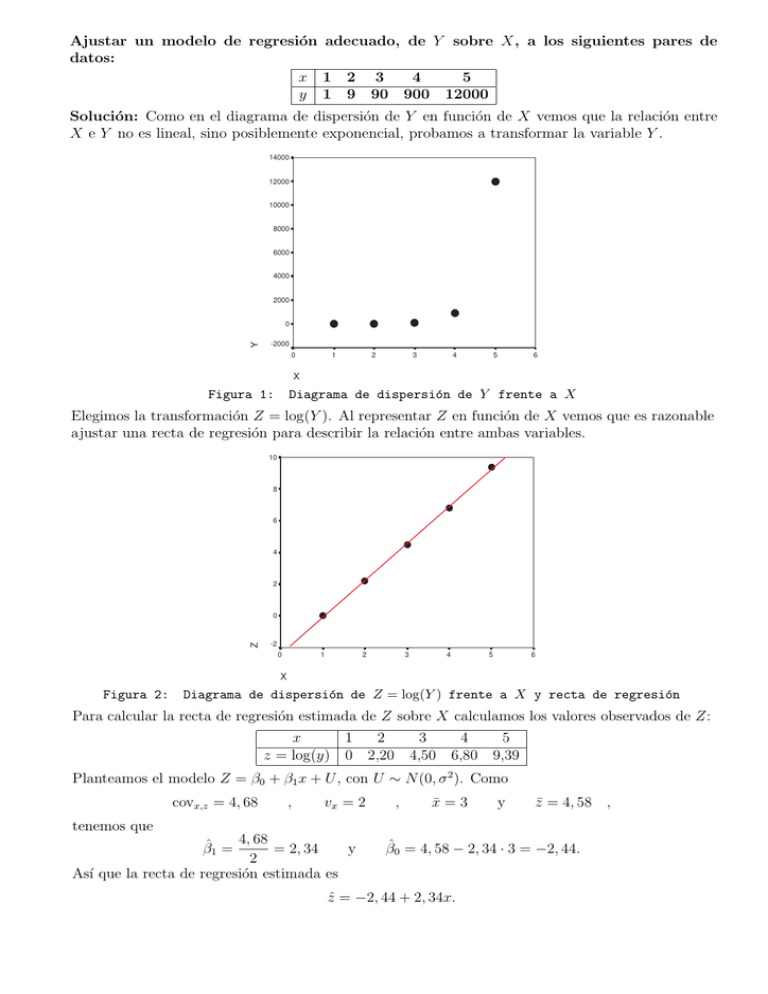
Ajustar un modelo de regresión adecuado, de Y sobre X, a los siguientes pares de datos: x 1 2 3 4 5 y 1 9 90 900 12000 Solución: Como en el diagrama de dispersión de Y en función de X vemos que la relación entre X e Y no es lineal, sino posiblemente exponencial, probamos a transformar la variable Y . 14000 12000 10000 8000 6000 4000 2000 Y 0 -2000 0 1 2 3 4 5 6 X Figura 1: Diagrama de dispersión de Y frente a X Elegimos la transformación Z = log(Y ). Al representar Z en función de X vemos que es razonable ajustar una recta de regresión para describir la relación entre ambas variables. 10 8 6 4 2 Z 0 -2 0 1 2 3 4 5 6 X Figura 2: Diagrama de dispersión de Z = log(Y ) frente a X y recta de regresión Para calcular la recta de regresión estimada de Z sobre X calculamos los valores observados de Z: x 1 2 3 4 5 z = log(y) 0 2,20 4,50 6,80 9,39 Planteamos el modelo Z = β0 + β1 x + U , con U ∼ N (0, σ 2 ). Como covx,z = 4, 68 , vx = 2 , x̄ = 3 y z̄ = 4, 58 , tenemos que 4, 68 = 2, 34 y 2 Ası́ que la recta de regresión estimada es β̂1 = β̂0 = 4, 58 − 2, 34 · 3 = −2, 44. ẑ = −2, 44 + 2, 34x.