M - CiberEsquina - Universidad Nacional Abierta
Anuncio
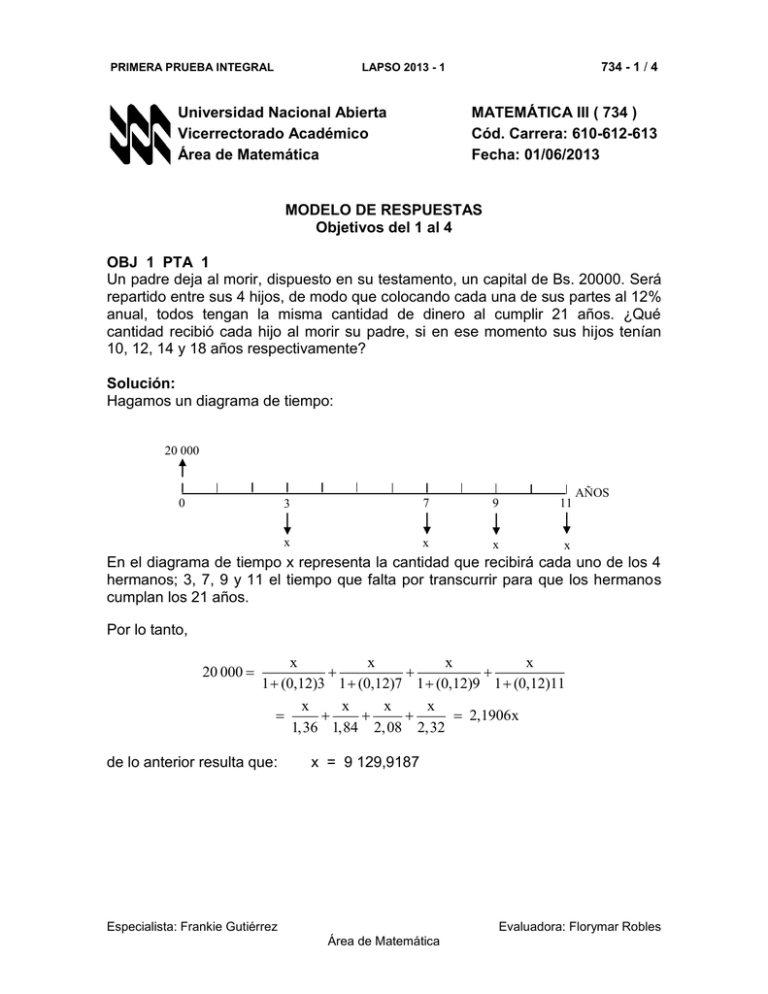
PRIMERA PRUEBA INTEGRAL 734 - 1 / 4 LAPSO 2013 - 1 Universidad Nacional Abierta Vicerrectorado Académico Área de Matemática MATEMÁTICA III ( 734 ) Cód. Carrera: 610-612-613 Fecha: 01/06/2013 MODELO DE RESPUESTAS Objetivos del 1 al 4 OBJ 1 PTA 1 Un padre deja al morir, dispuesto en su testamento, un capital de Bs. 20000. Será repartido entre sus 4 hijos, de modo que colocando cada una de sus partes al 12% anual, todos tengan la misma cantidad de dinero al cumplir 21 años. ¿Qué cantidad recibió cada hijo al morir su padre, si en ese momento sus hijos tenían 10, 12, 14 y 18 años respectivamente? Solución: Hagamos un diagrama de tiempo: 20 000 0 3 7 9 11 x x x x AÑOS En el diagrama de tiempo x representa la cantidad que recibirá cada uno de los 4 hermanos; 3, 7, 9 y 11 el tiempo que falta por transcurrir para que los hermanos cumplan los 21 años. Por lo tanto, 20 000 x x x x 1 (0,12)3 1 (0,12)7 1 (0,12)9 1 (0,12)11 x x x x 2,1906x 1,36 1,84 2, 08 2,32 de lo anterior resulta que: x = 9 129,9187 Especialista: Frankie Gutiérrez Evaluadora: Florymar Robles Área de Matemática PRIMERA PRUEBA INTEGRAL 734 - 2 / 4 LAPSO 2013 - 1 OBJ 2 PTA 2 a) Si por una inversión nos pagan el 24% convertible trimestralmente, ¿cuál será la tasa efectiva que deberán pagarnos si cambia de este modo el régimen de capitalización de intereses? b) Tres capitales de Bs. 1000, cada uno se coloca al 8% anual con capitalización anual, el primero durante n años, el segundo durante ( n 1 ) años y el tercero durante ( n 2 ). Entre los tres capitales se obtuvo un interés de Bs. 786,5. Calcular el tiempo que estuvo colocado el primer capital. NOTA: Para lograr el objetivo debe responder correctamente ambos literales. Solución: a) Para dar respuesta a esta pregunta emplearemos la fórmula: i e = 1 p p 1 , 4 0, 24 e = 1 1 4 e = 26,24% b) Sabemos que independientemente del sistema de capitalización, siempre es cierto que: M = C I. Si en particular tomamos C = C1 = C2 = C3 = 1000 e I = I1 I2 I3 = 786,5 resulta: M = 3( 1000 ) 786,6 =3 786,6. Por otra parte, 3 786,6= 1 000 ( 1,08 )n 1 000 ( 1,08 )n 1 1 000 ( 1,08 )n 2 3 786,6 = 1 000 ( 1,08 )n 1 ( 1,08 ) ( 1,08 )2 3,7866 = ( 1,08 )n 1 ( 1,08 ) ( 1,08 )2 = 3,2464( 1,08 )n Ln 1,1664 1,1663= ( 1,08 )n n= = 2. Ln 1,08 Por lo tanto, el primer capital estuvo colocado durante 2 años. Especialista: Frankie Gutiérrez Evaluadora: Florymar Robles Área de Matemática PRIMERA PRUEBA INTEGRAL 734 - 3 / 4 LAPSO 2013 - 1 OBJ 3 PTA 3 Una compañía de bienes raíces vendió una propiedad en Bs. 4000. Le hicieron un pago inicial de Bs. 1000 y el resto lo van a pagar en periodos semestrales, el primero de los pagos vence seis (6) meses después de la fecha de la venta. El interés que se carga en la operación es de 14% capitalizable semestralmente y la deuda se debe amortizar en cinco (5) años. ¿Cuál será el pago semestral requerido?, ¿cuál será el importe total de los pagos?, ¿cuánto se pagará por concepto de intereses? y ¿cuánto se pagó en total por la propiedad? Solución: Lo primero que tenemos que notar, es que esta es una renta constante. Lo segundo, es que la tasa dada es convertible semestralmente, por lo que tenemos que calcular la tasa periódica. En este caso, esa tasa periódica es del 7% semestral y n = 10 ( dos semestres por cinco años ). Lo tercero, identificar lo conocido, lo que deseamos conocer y la fórmula que debemos aplicar. Una vez dicho todo lo anterior, procedemos a resolver el problema, para lo cual usaremos que: a 1 - 1+ i - n A=T n i =T i sustituyendo: 1 - 1+ 0,07 - 10 a 3000 = T 10 0,07 = T = 7,0236T 0,07 3000 T= = Bs. 427,1313 7,0236 Por lo tanto, el valor de los pagos semestrales es de Bs. 427,1313. Para dar respuesta a la segunda pregunta, lo único que debemos hacer es multiplicar el valor del pago semestral Bs. 427,1313 por el número de pagos efectuados, que en nuestro caso es de diez (10), con lo cual resulta: Importe total de pagos = Bs. 4 271,3 La respuesta a la tercera pregunta es: Importe total de pagos - Deuda = 4 271,3 - 3 000 = 1 271,3 Para dar respuesta a la cuarta y última pregunta, notemos que: Pago total = Importe total + Pago inicial, sustituyendo: Pago total =Bs. 4 271,3 + Bs. 1 000 = Bs. 5 271,3 Especialista: Frankie Gutiérrez Evaluadora: Florymar Robles Área de Matemática PRIMERA PRUEBA INTEGRAL LAPSO 2013 - 1 734 - 4 / 4 OBJ 4 PTA 4 Una deuda de Bs 50000 con tasa preferencial del 21% efectivo anual, se debe amortizar en 4 años con el siguiente plan: cuotas semestrales iguales más cuotas extraordinarias de Bs F 5000 cada final de año. Calcular el valor de las cuotas y preparar la tabla de amortización correspondiente. Solución: Ver unidad 4, ejemplo 7 página 74 del problemario de Matemática III (cód. 734). FIN DEL MODELO DE RESPUESTAS Especialista: Frankie Gutiérrez Evaluadora: Florymar Robles Área de Matemática