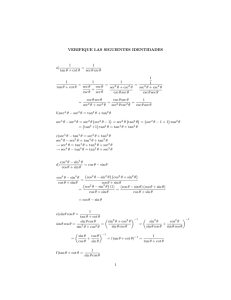
TRIGONOMETRIC IDENTITIES tanA = sinA/cosA secA = 1/cosA
Anuncio

TRIGONOMETRIC IDENTITIES tan A = sin A/ cos A sec A = 1/ cos A cosec A = 1/ sin A cot A = cos A/ sin A = 1/ tan A sin2 A + cos2 A = 1 sec2 A = 1 + tan2 A cosec 2 A = 1 + cot2 A sin(A ± B) = sin A cos B ± cos A sin B cos(A ± B) = cos A cos B ∓ sin A sin B tan(A ± B) = tan A ± tan B 1 ∓ tan A tan B sin 2A = 2 sin A cos A cos 2A = cos2 A − sin2 A = 2 cos2 A − 1 = 1 − 2 sin2 A tan 2A = 2 tan A 1 − tan2 A sin 3A = 3 sin A − 4 sin3 A cos 3A = 4 cos3 A − 3 cos A tan 3A = 3 tan A − tan3 A 1 − 3 tan2 A sin A + sin B = 2 sin A+B cos A−B 2 2 sin A − sin B = 2 cos A+B sin A−B 2 2 cos A−B cos A + cos B = 2 cos A+B 2 2 cos A − cos B = −2 sin A+B sin A−B 2 2 2 sin A cos B = sin(A + B) + sin(A − B) 2 cos A sin B = sin(A + B) − sin(A − B) 2 cos A cos B = cos(A + B) + cos(A − B) −2 sin A sin B = cos(A + B) − cos(A − B) a sin x + b cos x = R sin(x + φ), where R = If t = tan 1 x 2 √ a2 + b2 and cos φ = a/R, sin φ = b/R. 2t 1 − t2 then sin x = , cos x = . 1 + t2 1 + t2 cos x = 12 (eix + e−ix ) ; eix = cos x + i sin x ; sin x = 1 2i (eix − e−ix ) e−ix = cos x − i sin x