Parcia #1Control - Ingeniería Mecánica
Anuncio

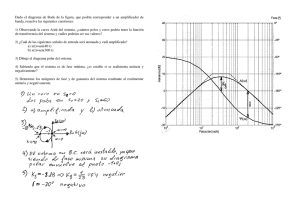
Parcia #3 - Sistemas de Control – Ing. Mecánica - 2015 Docentes: G. García; G. Oggier. Alumno: Nota: Para los problemas planteados resolver mediante las trazas asintóticas de bode. Problema 1: Para un sistema de control con realimentación unitaria cuya función de transferencia de trayectoria directa puede modelarse como G s 10 / s 1 s 4 , diseñar una acción de control del tipo PD por el método de la respuesta en frecuencia, para cumplir con las siguientes especificaciones: ts ≤ 1 seg y %OS ≤ 15%. Luego determinar el error en régimen permanente con y sin el compensador diseñado ante una entrada escalón unitario. Problema 2: Considere el sistema de la Figura 1. Diseñe compensador de atraso-adelanto tal que la constante de error estático de velocidad kV sea de 20 seg-1, el margen de fase sea de 60° y el margen de ganancia no sea menor que 8 dB. Figura 1 Problema 3: En la Figura 2-a se muestra un sistema masa-resorte-amortiguador. El diagrama de bode obtenido de manera experimental se muestra en la Figura 2-b. Determinar los valores numéricos de m, b y k. Figura 2 -a Figura 2 -b Recordar que para un sistema prototipo de segundo orden, el pico de resonancia puede determinarse con la siguiente expresión: Mr 1 2 1 2 . Formulas útiles: C ( s) n 2 2 R s s 2n s n 2 Prototipo 2 do. orden sx n jn 1 2 ts 4 AB 1 2 GAT ( s) Kc 2 4 4 4 2 2 T s 1 T s 1 1 % Sobrepaso e / tan 1 2 ts (2%) x 100 2 1 2 2 1 4 max 4 jmax T 1 1 jmax T 1 GAD (s) Kc T s 1 T s 1 0 1 4 n 1 T 1 sen m 1 sen m ln %OS /100 2 ln 2 %OS /100